二項ヒープでは次の操作ができます。\(n\) はヒープの要素数。
- insert(v)
- ならし \(O(1)\) 。ヒープに要素 \(v\) を追加する。
- find-min()
- 実時間 \(O(1)\) 。ヒープの最小要素を返す。
- delete-min()
- 実時間 \(O(\log(n))\) 。ヒープの最小要素を削除する。
- delete(v)
- 実時間 \(O(\log(n))\) 。要素 \(v\) を削除する。
- decrease-key(v, Δ)
- 実時間 \(O(\log(n))\) 。要素 \(v\) のキーを \(\Delta\) だけ減算する。
- meld(h₁, h₂)
- ならし \(O(1)\) 。ヒープ中の二つの木 h₁, h₂ を合体する。
- meld(h)
- ならし \(O(1)\) 。別のヒープ h と合体する。
二分ヒープでは insert が \(O(\log(n))\) 、meld が \(O(\log(n)^2)\) だったのが、二項ヒープではどちらも、ならし \(O(1)\) に改良されています。
二項木とは
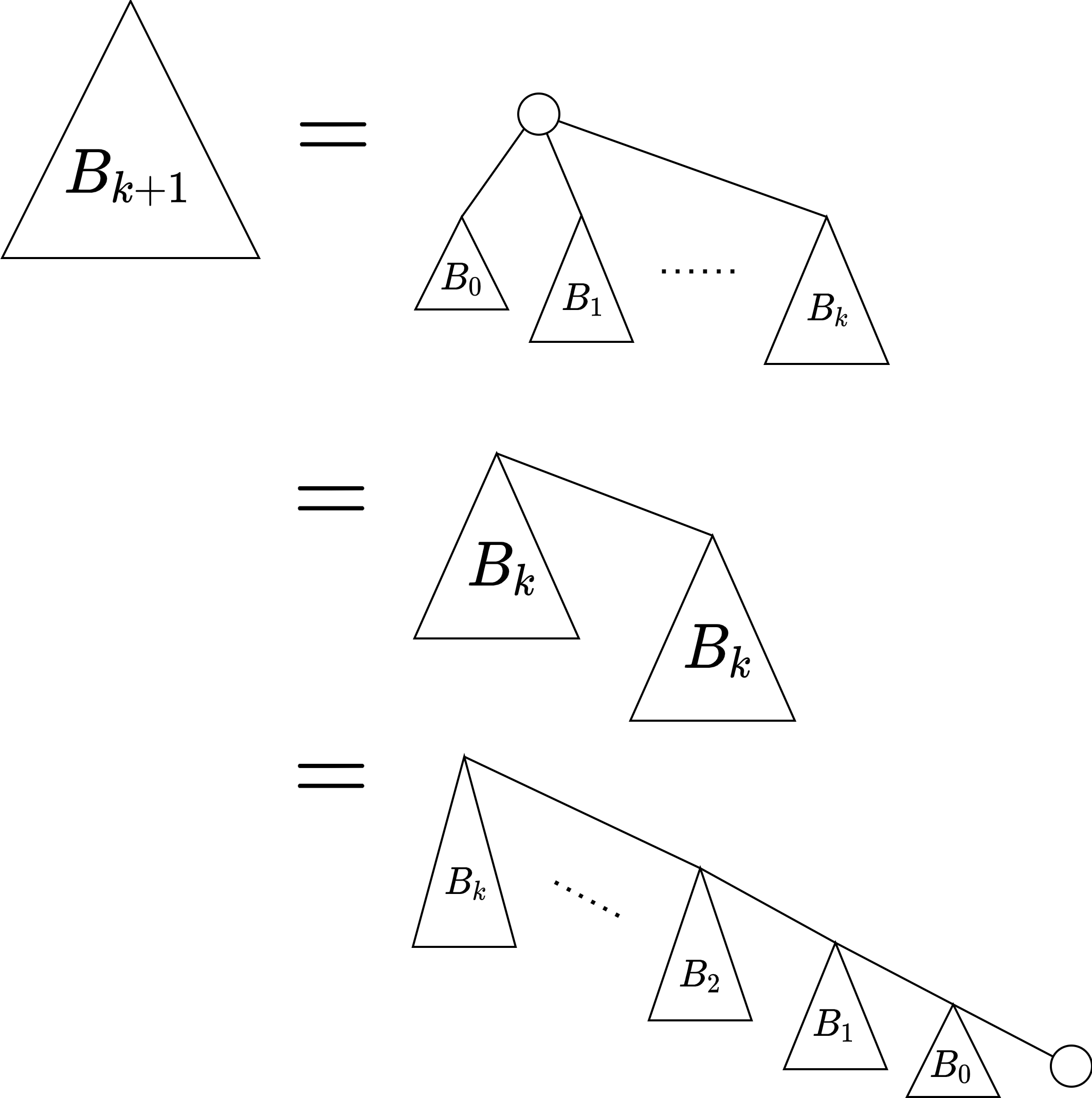
二項ヒープは、二項木 \(B_k\) という根付き木の列で表されます。定義は次の通り。
- \(B_0\) は 1 頂点からなる根付き木
- \(B_{k+1}\) は、根の子をそれぞれ新たな根とする部分木が \(B_0,B_1,\ldots,B_{k}\) である根付き木
\(B_0,B_1,B_2,B_3,B_4\) は下図のようになります。

帰納法から二項木 \(B_k\) は頂点数 \(2^k\) 、高さ \(k\) です。
帰納法から \(B_{k+1}\) の構成方法は下図の通り 3 つあります。
アルゴリズム
二項ヒープは heap-property(親要素≦子要素)を満たす、二項木の集合の列 \((L_i)\) からなります。根の次数が \(i\) の二項木は \(L_i\) に置きます。次数 \(i\) の二項木の頂点数が \(2^i\) なので、\(i \leq \log_2(n)\) です。
find-min
いずれかの根付き木の根が最小要素になっているので、その根へのポインタを持つことで、find-min は \(O(1)\) でできます。
meld
meld(h₁, h₂) は heap-property(親要素≦子要素)を満たすように、大きい方の根を小さい方の根の子として繋げば \(O(1)\) でできます。h₁ と h₂ の根の次数が等しいときにしか meld しないので、meld 後の根付き木もまた二項木です。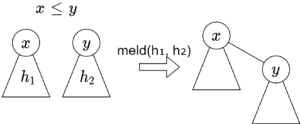 meld(h) は、delete-min において、meld する根付き木の列として新たに \(h\) を加えればいいです。つまり、根付き木の列は複数本ことになります。実際に meld するのは delete-min まで遅延させます。
meld(h) は、delete-min において、meld する根付き木の列として新たに \(h\) を加えればいいです。つまり、根付き木の列は複数本ことになります。実際に meld するのは delete-min まで遅延させます。
insert
insert(v) は、要素 \(v\) を一頂点の木として、\(L_1\) に加えれば \(O(1)\) です。一頂点の木は二項木 \(B_0\) です。
delete-min
delete-min() は、最小要素を削除したあと、その子を根とする部分木を新たに根付き木の列に加えま
。部分木は再度、二項木になります。根の次数が一意になるまで meld を繰り返します。その後、最小要素へのポインタを更新します。
計算量解析します。二項木 \(B_k\) の頂点数 \(2^k\) より、\(k \leq \log_2(n)\) です。従って、最小要素の子は \(O(\log(n))\) 個しか存在せず、切り離すのは \(O(\log(n))\) 時間でできます。二項木は insert 以外では増えないので、meld 前の二項木の個数は insert 回数 \(p\) で抑えられます。meld の度に二項木は一つなくなるので、meld 回数は高々 \(p\) 回です。\(L_1,L_2,\ldots,L_{\lfloor \log_2(n) \rfloor }\) を走査して、一意であることを確かめるには \(O(\log(n))\) 時間かかります。meld(h) によって追加された根付き木の列(配列)の空の部分を見ることにより、計算量は悪化しないでしょうか。根の次数 i を i ビット目、二項木の有無を 1/0 に対応させると、根付き木の配列は頂点数の二進表記になっています。insertのポテンシャルを2とすると、二進表記における、(0の個数)+(1の個数)×2のポテンシャルを常に持つので、ならせることが分かります。これは、\(1+\overbrace{1\ldots1}^{n\text{個}}=1\overbrace{0\ldots0}^{n \text{個}}\) のポテンシャルは \(2+2n-n=2+n\)、\(1+0=1\) のポテンシャルは \(2+1-1=2\) 、\(0+0=0\) のポテンシャルは \(1+1-1=1\) となることから示されます。以上より、insert で計算量をならすと、delete-min は \(O(\log(n))\) になります。
decrease-key(v, Δ)
要素 \(v\) で \(Δ\) だけ減算してから、heap-property(親要素≦子要素)を満たすまで、親と子を再帰的に交換する。二項木の高さ \(O(\log(n))\) 時間でできる。
delete(v)
decrease-key(v, -∞) として、\(v\) を根に持ってきてから、delete-min() で削除する。
参考文献
- 組合せ最適化(B. コルテ, J. フィーゲン )
- Fibonacci ヒープを実装しました(えびちゃん)
Comments