平衡括弧列の定義

平衡括弧列には同値な定義が様々あり、どの定義を使うかによって問題の解きやすさは劇的に変わる。平衡括弧列全体を \(\mathcal P\), 長さ \(2n\) の平衡括弧列全体を \(\mathcal P_{2n}\) と置く。

連結と再帰による定義

平衡括弧列とは、空文字列および、次の操作を繰り返すことで生成される文字列である。

• 二つの平衡括弧列 \(A, B\) を連結した文字列 \(AB\)
• 平衡括弧列 \(A\) を用いて \((A)\) と書ける文字列

(を x, ) を y と置くと、\(F = 1 + xFyF = 1 + xy + xyxy + \cdots\) の単項式であるものと言い換えることもできる。二つ目の操作を \()A(\) に置き換えた時に生成される文字列を負の平衡括弧列と呼ぶことにする。また、元の定義による文字列を正の平衡括弧列と呼ぶことにする。正の平衡括弧列を逆から読むと負の平衡括弧列になる。平衡括弧列をいくつかの極小な平衡括弧列の連結で表した時、その極小な平衡括弧列たちを既約平衡括弧列と呼ぶことにする。

\(\pm1\)列による定義

\((\), \()\) を \(+1, -1\) に置き換えた数列 \(\delta a\) の累積和 \(a_i = \sum_{k=1}^i \delta a_k\) について
\begin{eqnarray}
\left\{
\begin{array}{l}
a_{i+1} – a_i\in \{+1,-1\} \\
a_i \geq 0 \\
a_{0} = a_{2N} = 0
\end{array}
\right.
\end{eqnarray}が成り立つとき平衡括弧列と定義する。mod 2 で考えると、初めて \(a_i < 0\) となるのは \(i\) が奇数のときだけだと分かる。従って、\(a_{2i + 1} \geq 0\) で十分。\(a_i \geq 0\) を \(a_i \leq 0\) にすると負の平衡括弧列になる。累積和によって定義されていることから、\(\delta a\) の一点更新は \(a\) の区間更新に直すことになる。例えば、i 文字目を ( から ) に変更する操作は、区間 \([i..2N]\) に \(-2\) を足す操作になる。また、i 番目の ( と j 番目の ) を swap する操作は区間 \([i..j)\) に \(-2\) を足す操作になる。
\(0, 2\) 列による言い換え \begin{eqnarray}
\left\{
\begin{array}{l}
t_{i+1} – t_i\in \{0,2\} \\
t_{2i-1} \geq 2i \\
t_{0} = 0 \\
t_{2N} = 2N
\end{array}
\right.
\end{eqnarray} が有効な場合もある。

()の削除による定義

隣接する2文字()の削除を繰り返すことで空文字列にできる文字列を平衡括弧列と定義する。空でない極小な括弧列 \((A_1), (A_2), \ldots, (A_n)\) を用いて \((A_1)(A_2)\ldots (A_n)\) と書ける括弧列を、根の子の部分木が \(A_1, A_2, \ldots, A_n\) の表すそれである木に対応させると、子の順序を区別する n 辺の根付き木と一対一対応する。

• LCA（yuki1778）
• 二乗の木DP（DDCC2016C）

()の削除は、葉の削除に対応する。オイラーツアーの各辺について、一回目は (, 2回目はを ) に対応させると元の括弧列が得られる。右子・左子を区別する n 頂点二分木を平衡括弧列と一対一対応させることもできる。この場合、オイラーツアーの各頂点について、一回目は (, 2回目は ) に対応させる。この木の各辺を (, ) に対応させると、n + 1 個の元の積を二項演算として処理するための括弧付けと一対一対応する（これらの元に対応する頂点は、全2分木となるように葉として追加する）。

• 対応する括弧の添字は偶奇が異なることを示せ。
• N 箇所を白、N 箇所を黒で塗った長さ2Nの配列について、白と黒がペアになる括弧列が存在することを示せ。（ARC120D）
• 添字の集合 \(\{1,2,\ldots,N\}\) を2つの集合 A, B に分ける。A の偶数と奇数の個数は等しく、B の偶数と奇数の個数も等しい。A に含まれる添字の位置では { か }, B に含まれる添字の位置では ( か ) となるように平衡括弧列が構成できることを示せ（AGC048B, CF1593G）

経路による定義

(, ) を格子点 \((x, y)\) から \((x, y+1), (x+1, y)\) の移動と対応させる。括弧列を戦闘から読み込んだとき \(x \leq y \) の下、\((0, 0)\) から \((n, n)\) への移動経路になっているならば平衡括弧列と定義する。

45度回転させて、\((x, y)\) から \((x+1, y+1), (x-1, y-1)\) に \(y \geq 0\) の下、移動できるときの \((0, 0)\) から \((n, 0)\) への経路とすることもできる。以下の問題は経路によって視覚的にイメージした方が分かりやすいと思う。

• 巡回シフトで平衡括弧列にできるか線形で判定せよ (ARC138C)
• 巡回シフトで平衡括弧列にできるなら、そのうち、辞書順最小のものを求めよ（VK Cup 2015 Round 1 : A）
• 平衡括弧列となるような置換のうち、並び替え後の添字が辞書順最小のものを求めよ（ARC141C）
• 平衡括弧列となる部分文字列の個数を求めよ（2018 codeFlyer 本選 C）

\(y \geq 0\) を \(y \leq 0\) にすると負の平衡括弧列になる。任意の非空な括弧列は非空な正の平衡括弧列と非空な負の括弧列を交互に連結した文字列として一意に表せる。

ゲームによる定義

長さ \(2N\) の配列 \(\delta a\) について、先手と後手は交互に次の操作をする。

• 先手はまだ選ばれていない要素のうち、最も先頭に近いものを ( に置換する。
• 後手はまだ選ばれていない要素から好きなものを ) に置換する。

それ以上操作できなくなったときに生成される文字列を平衡括弧列と定義する（ARC138C）

平衡括弧列の個数

長さ \(2n\) の平衡括弧列は $$\frac{1}{n+1}{2n \choose n}$$個ある。この数を \(n\) 項目のカタラン数と呼ぶ。(, ) がそれぞれ \(n\) 個ある長さ \(2n\) の括弧列は \({2n \choose n}\) 個ある。これら全体を \(\mathcal{A_n}\)、長さ \(2n\) の平衡括弧列全体を \(\mathcal{B_n}\) とすると、ちょうど \(|\mathcal{A_n}| = (n + 1)|\mathcal{B_n}|\) であるから、何らかの \(\mathcal{A_n}\) 上の同値関係 \(\sim\) を取ると

• 同値類のサイズがそれぞれ \(n + 1\) となり、\(\mathcal{A_n}/\sim\) と \(\mathcal{B_n}\) の間の全単射がある。
• 同値類のサイズがそれぞれ \(\frac{1}{2n+1}{2n + 1\choose n}\) となり、ある同値類と \(\mathcal{B_n}\) の間の全単射がある。

のようなことが成り立つはずである。導出 3, 4 ではそのような同値関係を構成している。

カタラン数の導出1（鏡像法）

長さ \(2n\) の平衡括弧列は、\(y = x + 1\) を通らずに \((0, 0)\) から \((n, n)\) に移動する経路に対応付けられた。その経路数は鏡像法によって、\({2n \choose n}-{2n \choose n-1}\) だと分かる。\(y = x + A\) を通らずに移動する経路数は同様に鏡像法により \({2n \choose n}-{2n \choose n-A}\) である。先頭 \(A-1\) 文字が ( である長さ \(2n+A-1\) 文字の平衡括弧列の個数に等しい。

カタラン数の導出2（組合せ）

(, ) がそれぞれ \(n\) 個ある長さ \(2n\) の括弧列全体を \(\mathcal{A_n}\)、長さ \(2n\) の平衡括弧列全体を \(\mathcal{B_n}\) とする。また、\(1, -1\) がそれぞれ \(n-1, n+1\) 個ある括弧列全体を \(\mathcal{C}_n\) とする。非平衡括弧列 \(\mathcal{A}_n \setminus \mathcal{B}_n \) と \(\mathcal{C}_n\) の間の全単射を作る。

全単射（対合） : 累積和が初めて \(-1\) になった箇所を \(k\) 文字目として、\(k + 1\) 文字目以降の正負を反転させる。
カタラン数は \(|\mathcal{B}_n| = |\mathcal{A}_n|-|\mathcal{C}_n| = {2n \choose n}-{2n \choose n-1}\) となる。

写像\(\phi:(A_0)\ldots)A_k(\ldots(A_{2k} \mapsto A_0)\ldots)A_k)A_{k+1}(\ldots(A_{2k-1}\)により、(,)がn-1,n+1個でprefix min が負の括弧列と(,)がn-1,n+1個の括弧列の全単射ができる。要は一番下左の)(を))に変えている。括弧列wのmaj(w)を(,)を1,0で置き換えた列のmajとして定義すると、\(\mathrm{maj}(w)=\mathrm{maj}(\phi(w))+1\)。よって長さ2nの平衝括弧列のmajの母関数は\({2n \choose n}_q – q{2n\choose n-1}_q=\frac{1}{(n+1)_q}{2n \choose n}_q\)。

カタラン数の導出3（Bertrand’s ballot theorem）

\(+1, -1\) がそれぞれ \(n+1, n\) 個の列 \(\delta a\) は \({2n+1 \choose n}\) 個ある。部分列 \(\delta a_2, \delta a_3, \ldots, \delta a_{2n+1}\) が平衡括弧列になるには、\(\min a_i = 1\) でなくてはならない。\(\delta a\) の cyclic shift しのうち、そのような条件を満たすのは、\(\min a_i\) を達成する最後の位置を始点に持ってくる場合だけである。\(n, n+1\) が互いに素なことから、原始的な文字列なので cyclic shift で移る列は相異なる。従って、cyclic shift で移り合う列全体を同値類とみなすと、平衡括弧列の個数は $$\frac{1}{2n+1}{ 2n+1 \choose n} = \frac{1}{n+1}{2n \choose n}$$ 個である。円環において)(を削除して最後に残った１つが始点という見方もできる。

[類題]
互いに素なs,rについて、重みrの(をs個、重み-sの)をr個、prefix sumが非負になるように並べる方法の数も同様に計算できる。最小値が先頭に来るように巡回シフトすれば良い。重み0の非自明な部分和が存在しないことと、原始的な文字列であることから一つに定まる。[類題]重み1の(と重み-sの)を並べる方法であってprefix sumが非負の個数も同様に数えられる。これは、円環において)で終わる和0の極小な部分文字列を削除すればよい。

カタラン数の導出4（Chung-Feller） :

Young-Ming Chenによる証明。

• \(\varphi^{} : L)A(R \mapsto A(L)R\)
  • \(L\) は平衡括弧列、\(A\) は負の平衡括弧列

\(\varphi\) は全単射で、\(\varphi\) を作用させると負の平衡括弧列の長さが \(2\) 減る。従って、負の平衡括弧列の長さで同値類を作ると、各同値類の大きさは等しい。平衡括弧列は負の平衡括弧列の長さが \(0\) の同値類をなすから、\(\frac{1}{n+1}{2n \choose n}\) 個ある。以下のように母関数を用いて示すこともできる。\(f(x)=\frac{1-\sqrt{1-4x}}{2x}\) と置くと
\(\begin{align}
&\frac{1}{1-(xf(x)+txf(tx))} \\
=&\frac{1}{\sqrt{1-4x}+\sqrt{1-4tx}} \\
=&\frac{\sqrt{1-4tx}-\sqrt{1-4x}}{4x(1-t)} \\
=&\sum_i a_i x^{i}\frac{1-t^{i+1}}{1-t}
\end{align}\)

カタラン数の導出5（母関数）

平衡括弧列となる極小な接尾辞を \((A)\) 、残りの文字列を \(B\) とすると、\((A)B\) の形になる。\(A, B\) もまた平衡括弧列だから、\(A\) と \(B\) の長さを \(2i, 2(n-i-1)\) とすると
$$C_{n}=\sum_{i=0}^{n-1} C_i C_{n-1-i}, \quad C_0 = 1$$ が成り立つ。カタラン数の母関数を \(f(x):=\sum C_ix^i\) と置く。漸化式の両辺に \(x^n\) を掛けて \(n \geq 1\) について和を取ると、$$f(x)-1 = xf(x)^2$$ となる。\(f(x)\) について解くと \(f(x) = \frac{1 \pm \sqrt{1-4x}}{2x}\) を得る。\([x^0] f(x) = 1\) より \(f(x) = \frac{1- \sqrt{1-4x}}{2x}\) である。二項定理によって展開すると、\begin{align}
f &= -\frac{1}{2}\sum_{i=1}^\infty {\frac{1}{2} \choose i}(-4)^ix^{i-1} \\
&=\sum_{i=1}^\infty -\frac{1}{2}\frac{1}{2}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right) \cdots \left(-\frac{2i-1}{2}\right)(-4)^i\frac{1}{i!}x^{i-1} \\
&=\sum_{i=1}^\infty\frac{1}{2}\cdot1\cdot3\cdot5\cdots (2i-1) 2^i \frac{1}{i!} x^{i-1} \\
&=\sum_{i=1}^\infty\frac{1}{2}\frac{(2i)!}{i!i!} x^{i-1} \\
&=\sum_{i=1}^\infty C_{i-1} x^{i-1} \\
\end{align} となる。

カタラン数の畳み込み

k 個畳み込んだカタラン数を
$$C_{n, k}=\sum_{n=\sum_{i=1}^k n_i} \prod_{i=1}^k C_{n_i}$$
と置く。例えば \(C_{n,4}\) は平衡括弧列 \(A, B, C, D\) (空文字列を許す) の組であって、長さの和が \(2n\) であるものの個数に等しい。

\(n\) 個の ( と \(n+k\) 個の ) とからなる括弧列全体を \(\mathcal{A}_{n, k}\) と置く。\(\mathcal{A}_{n, k}\) の各元は \(k\) 個の平衡括弧列 \(A_1, A_2, \ldots, A_k\) を用いて \( A_1)A_2)\ldots )A_k\) と一意に書ける。逆に \(k\) 個の平衡括弧列 \(A_1, A_2, \ldots, A_k\) は間に ) を挿入することで \(n\) 個の ( と \(n+k\) 個の ) からなる括弧列になる。

鏡像法などにより $$C_{n, k}=|\mathcal{A}_{n, k}| = {2n+k-1 \choose n}-{2n+k-1 \choose n-1} = \frac{k}{n+k}{2n+k-1 \choose n}$$ となる（KUPC2020M, yuki1662）

\(0 < a_1 < a_2 < \cdots < a_k < n\) を満たす整数列 \(a\) の個数を数える際に、
$$0 \leq a_1-1 \leq a_2-2 \leq \cdots \leq a_k-k \leq n
-k-1$$
として \( < \) を \(\leq\) に直す技術に似ていると思う。ラグランジュの反転公式でも示せる。\(f = xf^2+1\) と置く。\(h = f-1\) と変数変換すると \(h = x(h+1)^2\) である。
\begin{align}
[x^n]f^k =&\frac{1}{n}\frac{1}{2\pi i} \oint \frac{1}{x^n}\frac{d f^k}{dx} dx \\
=&\frac{1}{n}\frac{1}{2\pi i} \oint \frac{1}{x^n}\frac{d (h+1)^k}{dx} dx \\
=&\frac{1}{n}\frac{1}{2\pi i} \oint \frac{(h+1)^{2n}}{h^n}k (h+1)^{k-1}\frac{dh}{dx} dx \\
=&\frac{1}{n}\frac{1}{2\pi i} \oint \frac{(h+1)^{2n}}{h^n}k (h+1)^{k-1} dh \\
=&\frac{1}{n} [h^{n-1}] (h+1)^{2n+k-1}k \\
=&\frac{k}{n} \binom{2n+k-1}{n-1}
\end{align}

非平衡括弧列

非平衡括弧列 \(S\) は平衡括弧列 \(A_1, A_2, \ldots, A_n\) を用いて $$S = A_1)A_2)\ldots)A_k(\ldots(A_{n-1}(A_n$$ の形に一意にできる。括弧列に何らかの操作をして、平衡括弧列にするための最小操作数は、この形で考えると見通しが良いことが多い。括弧列 \(A,B\) に対応する \(\pm 1\) 列を \(\delta a, \delta b\) とする。上記の形における ) の個数は \(-\min a_i\) に等しく、( の個数は \(a_{2N}-\min a_i\) に等しい。\(b\) も同様。両方が 0 になると平衡括弧列である。\(AB\) に対応する \(\pm 1\) 列を \(\delta c\) とすると、
\begin{align}
&c_{2N} = a_{2N} + b_{2N} \\
&\min c_i = \min(\min(a_i), a_{2N}+\min(b_i))
\end{align}
となる。従ってモノイドになり、セグメント木に乗る。

• 平衡括弧列となる部分列の長さの最大値
• 平衡括弧列となるために必要な最小の削除回数
• 平衡括弧列となるために必要な最小の次の操作数：区間を選び、並びを逆にした後、( を ) に、) を ( にする(CodeSprint13D, SRM688Div1Easy)
• ?, (, ) からなる文字列について、? を置き換えることで平衡括弧列にできるか。（MUJIN2016D）
  • この問題については、0, 2 列で考える方針も良いと思う。

いくつかの文字列を並び替えて連結したあと、平衡括弧列になるように削除すべき文字の個数は次のように最小化できる。

\(\sum a_i \geq 0\) ならば \(\min(a_i)\) の降順につなげる。
\(\sum a_i \leq 0\) ならば \(\min(a_i)\) の昇順につなげる。

(ABC167F, AOJ2681, yuki684)

非平衡括弧列は、正の平衡括弧列と負の平衡括弧列が交互に現れる列として一意に表せる（ARC141C）。

ベクトル

平衡括弧列の \(\pm 1\) 列は \(2N\) 次元のベクトルと捉えるとよいことがある。平衡括弧列の区間は \(\mathbb{F}_2\) 係数 \(2N\) 次元ベクトル空間の部分空間をなす。例えば \(a \leq b \leq c \leq d\) について、\(S[a .. c]\) と \(S[b..d]\) が平衡括弧列ならば、\(S[a..b), S[b..c], S(c..d]\) は平衡括弧列である（SRM688Div1M）。二つの平衡括弧列の \(\pm 1\) 列 \(\delta a, \delta b\) について、\(\delta c=\delta a-\delta b\) は \(\pm2, 0\) からなる列で、\(c_1=c_{2N}=0\) である。逆に、\(c_1=c_{2N}=0\) を満たす任意の \(\pm 2, 0\) からなる列 \(c\) からある平衡括弧列の \(\pm 1\) 列 \(\delta a, \delta b\) が構成できる（CODE FESTIVAL 2017 Elimination Tournament : C）

マトロイド

任意の2つの平衡括弧列 A, B は、どのように A, B 間の転倒数を減らす隣接swapを A にしても、バランスが保たれる。従って、平衡を保ちながら転倒数回で A を B にできる。また、任意の相異なる2つの平衡括弧列 \(A, B\) は、A のある二つの文字をスワップすることで編集距離を2つ小さくできる。従って、(の位置の集合はマトロイドをなす。似た話として、oとxをそれぞれa,b個並べる方法であって、oが隣接しないようなものは、oの位置の集合がマトロイド交差をなす。台集合\(E=[a+b]\)に対して独立集合族を\(\{F \subseteq E : \text{$\{2i,2i+1\} \not\subseteq F$ for all $i$}, |F| \leq b\} \)とするマトロイドと独立集合族を\(\{F \subseteq E : \text{$\{2i-1,2i\} \not\subseteq F$ for all $i$ }, |F| \leq b\} \)とするマトロイドのマトロイド交差。

最大重み括弧列問題

• \(i\) 文字目が ( ならば \(p_i\) 点、) ならば \(-p_i\) 点を得る。長さ \(2N\) の平衡括弧列の場合、得点は最大何点か（えこってさんの提出）。
  (, ) を \(1, -1\) で置き換えた数列を \(\delta a\), \(0, 2\) で置き換えた数列を \(\delta b\) とすると、\(p \cdot \delta a = p \cdot \delta b-2N\) なので、\(p\) と \(\delta b\) の内積の最大値を求めればよい。交換定理より、どの二つの文字をスワップしても重みが小さくなるような括弧列が求めるべきものである。従って、\(p_i\) の大きい順に採用できるか見ていく貪欲法が回る。また別の方法として、\(i=1,3,5,\ldots,\)に対して、順に \(b_i \geq i+1\) を満たすまで、\(1,2,\ldots, i\) のうちまだ採用していない添え字であって、\(p_i\) 最大のものを ( に置き換える方法もある。
• (, ), x からなる長さ \(2N\) の文字列であって、x を除くと、平衡括弧列になる文字列を考える。\(i\) 番目が ( ならば \(p_i\) 点、x ならば \(0\) 点、) ならば \(-p_i\) 点を得る。最大何点を得るか（ABC250G）。(, x, ) を \(0, 1, 2\) に置き換えた数列を \(\delta s\) とすると、問題の文字列の条件は
  \begin{eqnarray}
  \left\{
  \begin{array}{l}
  s_{i+1} – s_i\in \{0,1,2\} \\
  s_i \geq i \\
  s_{0} = 0 \\
  s_{2N} = 2N
  \end{array}
  \right.
  \end{eqnarray}と言い換えられる。\(s, p\) の内積を最大化すればよい。\(\delta s\) を \(0\) で初期化する。明らかに、\(i=1, 2, \ldots, \) について順に \(s_i \geq i\) が等号で成り立つまで、まだ2回採用していない \(1, 2, \ldots, i\) のうち \(p_k\) が最大のものを選び、\(a_k \leftarrow a_k + 1\) とすればよい。

平衡括弧列のなす束

長さ \(2n\) の平衡括弧列 \(a, b\) について、\(a_i \leq b_i\) \((1 \leq i \leq 2n)\) のとき \(a \leq b\) と定める。このとき、\((a \lor b)_i = \max(a_i, b_i), (a \land b)_i = \min(a_i, b_i)\) となって束をなす(ref)。この束は、山がただ一つの平衡括弧列（位置も持つ）の集合の順序イデアルの束としてみなせるから、Birkhoffの表現定理より、分配束である。分配束なので、階層的である。ランクは転倒数（パスの面積）に等しい。転倒数が減少するような隣接要素の swap を繰り返すことで括弧列 a を b にできるとき、\(a < b\) として定めたposetとも捉えられる。また、隣接要素に限らない swap を許すような poset も考えることができる。しかし、これは束ではない。((()))() ∨ ()((())) が ((())()) か (()(())) で定まらない。

様々な変換

\(A,B,C,D,F \in\mathcal P\) とする。
接頭辞和が負になることのある、(, )が同数含まれる括弧列と、接頭辞和が一度も負にならず、(の方が)より正の偶数個多い括弧列との間の全単射は \(A)B)C(D(E \leftrightarrow A)B)C)D)E\) で構成できる。任意の接頭辞和が非負かつ先頭以外で
零になることのある括弧列と、接頭辞和が先頭以外では正の括弧列との間の全単射は
\((A)B(C(D \leftrightarrow (A(B(C(D\)でできる（ref）
\(()^{a_1}()^{a_2} \cdots ()^{a_n}\) の形で表したとする。すると、\(b_i = 1-a_i\) で定義される数列は接頭辞和が非負、 和が \(0\) の、各項が 1 以下の整数列になる。逆にそのような整数列はある正規括弧列と対応するので一対一対応がある。(がr個)がs個からなる括弧列を考える(r < s)。与えられた括弧列に対して、異なる文字が隣接する箇所の集合がsupersetになっていて、(が連続しないものが取れる。これは、円環において、(()()()()())という形の文字列を()()()()()()にすればよい。同じ文字が隣接しないこのような括弧列はマトロイドをなす（ABC218H）。

回避順列との全単射

312回避順列

各 ) に対応する ( が何個目の ( かを左から順に並べると 312回避順列になる。これは312 回避順列であることと、ある \(p, q \in Av(312)\) を用いて \((p \ominus1)\oplus q\) と書けることが同値だからである。\(w \ \in \mathcal{P} \Leftrightarrow \exists a,\exists b \in \mathcal{P}, w = ab \lor w = (a)\) と対応している。1, 2, .., n のデカルト木と対応付けてもよい。

321回避順列

まず、() については、 隣接する ( と ) をペアにする。その他の ) については、左から順にみていき、まだ割り当てられていない最も左の ( を割り当てる。各 ) について割り当てられた ( が左から何個目かを、左から順に並べると 321回避順列と一対一対応する。これは、321回避順列であることと、2つの増加列に順列が分解できることが同値だからである。Dyckパスを思い浮かべると分かりやすいと思う。

連分数

ステップ \(A = (1, 1), B = (1, -1)\) を使って、\((0, 0)\) からある \((n, 0)\) に \(y = -1\) を通らないように移動するパスを Dyck パスと呼びます。
高さ \(y = i\) から \(y = i + 1\) へ移動するときの重みを \(a_i\)、\(y=i+1\) から \(y=i\) へ移動するときの重みを \(b_i\) として、パスの重みを各移動の重みの積とすると、その母関数は、$$\frac{1}{1-\frac{xa_1b_1}{1-\frac{xa_1b_2}{1-\ddots}}}$$となります。

$$
\frac{a\frac{u}{v}+b}{c\frac{u}{v}+d} = \frac{au + bv}{cu+dv} \\
$$
なので、一次分数変換 \(\phi_i(z) = \frac{a_iz+b_i}{c_iz+d_i}\) の合成 \(\phi_1 \circ \phi_2 \circ \phi_3 \circ \cdots \) は行列積

$$\begin{pmatrix}
a_1 & b_1 \\
c_1 & d_1
\end{pmatrix}\begin{pmatrix}
a_2 & b_2 \\
c_2 & d_2
\end{pmatrix}\begin{pmatrix}
a_3 & b_3 \\
c_3 & d_3
\end{pmatrix} \cdots $$
で表せます。

ARC164F simple solitaire は \(a_i = i, b_i = i + 1\) としたときです。ただし、A の直後の B の重みは例外的に 1 とするので、\(\phi_i(z) = 1- a_ib_ix\left(\frac{1}{z}-1\right)-a_ix\) となります。

sum=0とprefix sum≠0の全単射

(,)がそれぞれn個ずつある括弧列のうち、prefix sum が非零の括弧列と、prefix sum が総和以外非零の括弧列の間の全単射を構成する。ここから\(\sum_k {2k \choose k}{2(n-k) \choose n-k} = 2^{2n}\) の全単射が構成できる（略）。prefix sum が負の括弧列は
\()A_1)\cdots)A_{2k}\) と書ける。総和が0で)から始まる括弧列は \()A_1)\cdots)A_k(\cdots (A_{2k}\) と書ける。ここから全単射があるのは自明だろう。
\(f=1+xf^2\) として、
\(\frac{1}{\sqrt{1-4x}}=\frac{1}{1-2xf}=\frac{f}{f-2xf^2} = \frac{f}{1-xf^2}\) という式を数え上げで説明した。

Narayana数

長さ2nの平行括弧列のうち、()がk個あるものをN(n,k)と置く。Narayana数と呼ぶ。平衡括弧列である極小なprefixの長さが2であるか否かで場合分けすることで母関数\(f=\sum_{n \geq 1}\sum_{k \geq 1}N(n,k)x^nt^k\)は\(f=(xf+xt)(1+f)\)と表せる。\(N(n,k)\)はサイクルシフトや、一番下の)(を((に変えるbijectionなどにより\(N(n,k)=\frac{1}{n}{n \choose k}{n \choose k-1}\)と求まる（二つ目の方法は、q類似も求まる）。

非交差分割

[n]の非交差分割の集合を\(\mathrm{NC}_n\)と置く。\(\mathrm{NC}_n\) と長さ 2n の平衡括弧の間に全単射がある。思いつきやすいのは、prefix が平衡括弧列となる箇所の集合を \(1\) を含むブロックと対応付ける方法だろう。もう一つの方法は、先頭の \((A_1(A_2(\cdots( A_i())\cdots))\) の \((\) の箇所を \(1\) を含むブロックと対応付ける方法（Callan）。これは、葉がn個の全２分木の各sprigをブロックに対応付けている。

\(\pi \in \mathrm{NC}_n\)について、その重み\(g(\pi)\)を数列\(g\)によって \(\prod_{B \in \pi} g_{\#B}\) と定義する。このとき、\(F(x)=\sum_{n \geq 1} \sum_{\pi \in \mathrm{NC}_n}g(\pi)x^n, G(x) = \sum_{n \geq 1}g_nx^n\) と置くと、\(F(x) = G(xF(x)))\) である。証明は、\(1\) を含むブロックを\(\{a_1, a_2, \ldots, a_k\}_{<}\) と置くと、そのほかのブロックは \(\{a_{i}+1, a_{i}+2, \ldots, a_{i+1}-1\}\) \((1 \leq i \leq k)\) の非交差分割で書けるからである。ただし、\(a_{k+1}=n+1\) とする。このとき、Lagrange反転により \([x^n]F(x)=[x^{-1}] G(x)^{n+1}x^{-1}/(n+1)\) である。

k重のdyck path

k個の長さ2nの平衡括弧列 \(s_0, s_1, \ldots, s_{k-1}\) であって、任意の地点の prefix sum が \(s_0, s_1, \ldots, s_{k-1}\) の順に広義単調増加になるようなものの個数を求めたい。\(i=1,2\ldots,k\)について\(s_i\)を\(\mathtt{(}^is_i\mathtt{)}^i\)で置き換えると、非交差経路の数え上げになり、LGV公式により以下のように計算できるKrattenthaler。
\begin{align}
&\det_{0 \leq i, j < k} C_{n+i+j} \\
=&\det_{0 \leq i, j < k} 2^{n+i+j} \frac{1\cdot3\cdot5\cdots(2(n+i+j)-1)}{(n+i+j)!} \\
=&2^{n^2}\det_{0 \leq i, j < k} \frac{(-\frac{1}{2}+1)\cdot(-\frac{1}{2}+2)\cdots(-\frac{1}{2}+(n+i+j))}{(n+i+j)!} \\
=&2^{n^2}\frac{\prod_{i=0}^{k-1}\left(-\frac{1}{2}+1\right)\cdot\left(-\frac{1}{2}+2\right)\cdots\left(-\frac{1}{2}+(n+i)\right)}{(n+k-1)!(n+k)!\cdots(n+2(k-1))!}\det_{0 \leq i, j < k} \left(-\frac{1}{2}+n+i+1\right)\cdot\left(-\frac{1}{2}+n+i+2\right)\cdots\left(-\frac{1}{2}+(n+i+j)\right)(n+i+j+1)(n+i+j+2) \cdots (n+i+(k-1)) \\
=&2^{n^2}\frac{\prod_{i=0}^{k-1}\left(-\frac{1}{2}+1\right)\cdot\left(-\frac{1}{2}+2\right)\cdots\left(-\frac{1}{2}+(n+i)\right)}{(n+k-1)!(n+k)!\cdots(n+2(k-1))!}\det_{0 \leq i, j < k} (x_i + a_1)(x_i + a_2)\cdots(x_i + a_j)(x_i+b_{j+1})(x_i+b_{j+2})\cdots(x_i+b_{k-1}) \\
=&2^{n^2}\frac{\prod_{i=0}^{k-1}\left(-\frac{1}{2}+1\right)\cdot\left(-\frac{1}{2}+2\right)\cdots\left(-\frac{1}{2}+(n+i)\right)}{(n+k-1)!(n+k)!\cdots(n+2(k-1))!}\prod_{0 \le i \leq j < k}(x_i-x_j) \prod_{1 \leq i \leq j \leq k-1} (a_i-b_j)\\
\end{align}

最後は \(x_i=n+i,a_i=i-1/2,b_i=i+1\) と置いた。以下のような変形を用いた。

\(j\)列目から\(j+1\)列目を引くことを\(j=1,2,\ldots,k-2\)の順に行うと
\begin{align}
&\det_{0 \leq i, j < k} (x_i + a_1)(x_i + a_2)\cdots(x_i + a_j)(x_i+b_{j+1})(x_i+b_{j+2})\cdots(x_i+b_{k-1}) \\
=&\prod_{j=1}^{k-1}(a_j-b_j)\det_{0 \leq i, j < k} (x_i + a_1)(x_i + a_2)\cdots(x_i + a_{j-1})(x_i+b_{j+1})(x_i+b_{j+2})\cdots(x_i+b_{k-1})
\end{align}
となる。これを繰り返すと、\(\prod_{1 \leq i \leq j \leq k-1}^{k-1}(a_i-b_j)\det_{0 \leq i, j < k} (x_i+b_{j+1})(x_i+b_{j+2})\cdots(x_i+b_{k-1})\)となり、あとはVandermonde行列の場合と同じ。

括弧列をDyckパスに移し、i番目のDyckパスとi-1番目のDyckパスの間にiを書き込むと、形が\((n-1,n-2,\ldots,1)\)で0, 1, .., kが書き込まれたplane partitionとの全単射ができる。このplane partitionを3次元図形に移して、横から見たときの図形から、また別種の非交差経路の数え上げに帰着出来て、\(\det_{0 \leq i, j < k} C_{n+i+j} = \det_{0 \leq i, j < n} {k+i+j \choose 2j}\) となる（Cigler, Feng）。

広義単調減少列の数え上げ

長さ \(N\) の広義単調減少整数列 \(M \geq \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_N \geq 0\) が与えられたとき、任意の \(i\) について \(\lambda_i \geq a_i \geq 0\) を満たす広義単調減少列 \(a\) の個数 mod \(P\) を \(O((N+M)\log(N+M)^2)\) で求めるnoshi91さんの手法があるが、LGV公式で個数を表してみる（Theorem 10.7.1）。この方針で高速に計算できるかは分からなかった。

まず、一般論として、平面分割と非交差経路の全単射が知られている（出題例）。平面分割とは、非負整数配列 \(\pi = (\pi_{i,j})_{i,j\geq 1}\) であって行・列方向に広義単調減少かつ非ゼロ要素が有限個であるもののこと。

例えば、以下のような平面分割を考えます。右上が(1, 1)です。

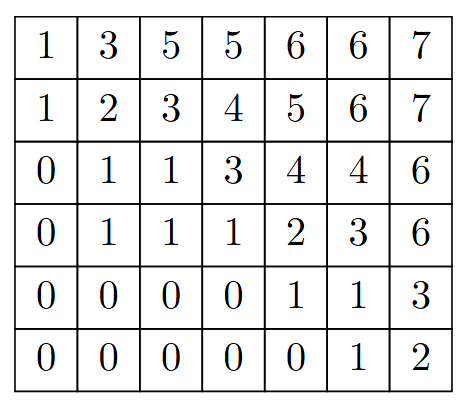
\((i,j)\) に \(\pi_{i,j}\) 個の直方体を積んだ図形（３次元ヤング図形）は下のようになります。

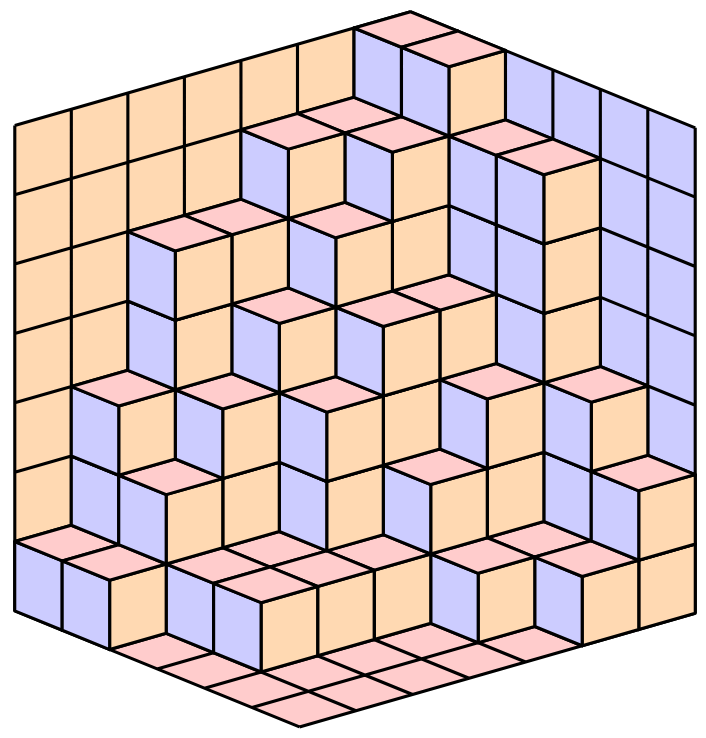
三次元ヤング図形は下図のように非交差経路と全単射が構成できます。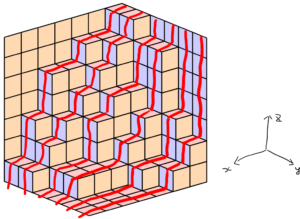

y軸方向から見た平面分割を考えて、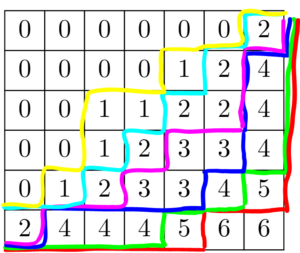パスを(1,1,0)方向に重ならないようにずらしたと考えても良いです。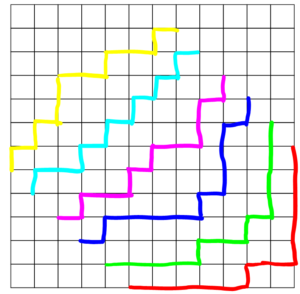

さて、単調減少列 \(a\) は非負要素を \(\pi_{i,1} = a_i\) と定めた平面分割と見なせるので、LGV公式により数え上げられます（Theorem 10.7.1）。\(\chi_{i}=\lambda_{N-i+1}\) と置くと \(N\) 個の非交差パスは \(i=1,2,\ldots,N\) について始点が \((-i, i-1)\), 終点が \((-i+1, \chi_{i}+i-1)\) なので、その個数は \(\det_{1 \leq i, j \leq N} {((\chi_{j} + j-1) – (i-1))+(-j-(-i+1)) \choose -j-(-i+1)} = \det_{1 \leq i, j \leq N} {\chi_{j} +1 \choose i-j+1}\) となる。例えば、\(a=(7,7,6,6,3,2), \lambda = (7,7,7,6,5,4)\) ならば下図のような非交差パスを考えています。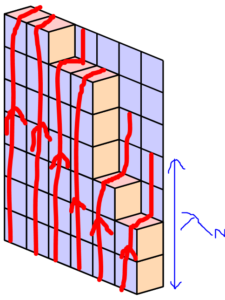

行列 \(W=\left({\chi_{j} +1 \choose i-j+1}\right)_{1 \leq i,j\leq n}\) は \(j-i > 1\) となる \((i,j)\) 成分が 0。従って、\(\prod_{i=1}^n W_{i, \tau(i)}\) が非ゼロとなる置換 \(\tau\) はある \(1=s_1 < \cdots < s_k = n+1\) を用いて、\(\begin{eqnarray} \tau(i) = \begin{cases}
s_{j-1} & (\text{if $i = s_{j}-1$ for some $j$} ) \\
i+1 & ( \text{otherwise} )
\end{cases}
\end{eqnarray}\)と書ける。そのような全ての整数列 \(s\) について \(\prod(-1)^{k}{\chi_{s_{i}}+1 \choose s_{i+1} – s_{i}}\) の和を取り、\((-1)^n\) を掛ければよい。さて、この方針で高速に求まるのだろうか？