見る方向を \(x\) 軸と \(y\) 軸で入れ替えると、効率的に解ける問題を集めてみました。
Floor Sum
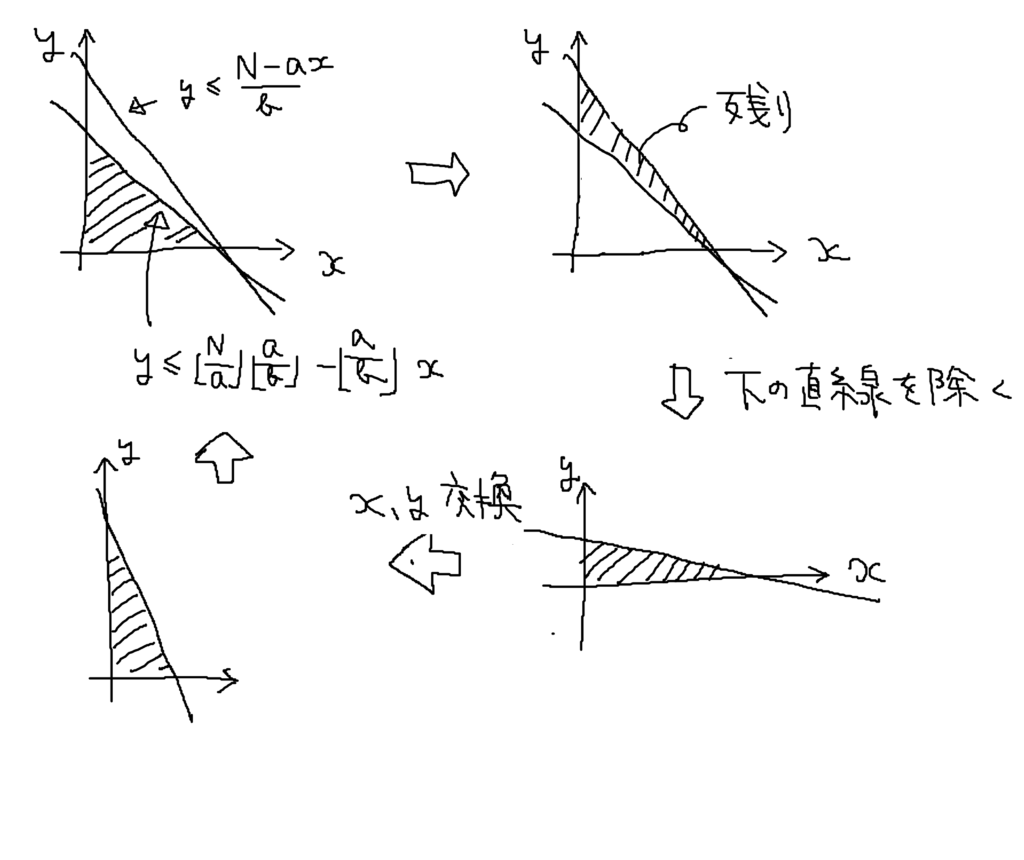
\(ax+by \leq N, a,b,N \in \mathbb{N}, x,y \geq 0\) を満たす格子点の数を求めてくださいという問題を考えます。\(x\) 軸に沿って格子点を大雑把に求めた後、\(y\) 軸に沿って格子点を求め、また \(x\) 軸に沿って…というようにすると効率的に求まります。
Grundy数（AGC002E）
それぞれ \(a_1, \ldots, a_N\) 個のキャンディからなる山が N 個あります。交互に次の操作を行い、最後のキャンディーを食べたほうが負けです。どちらが勝つでしょうか。
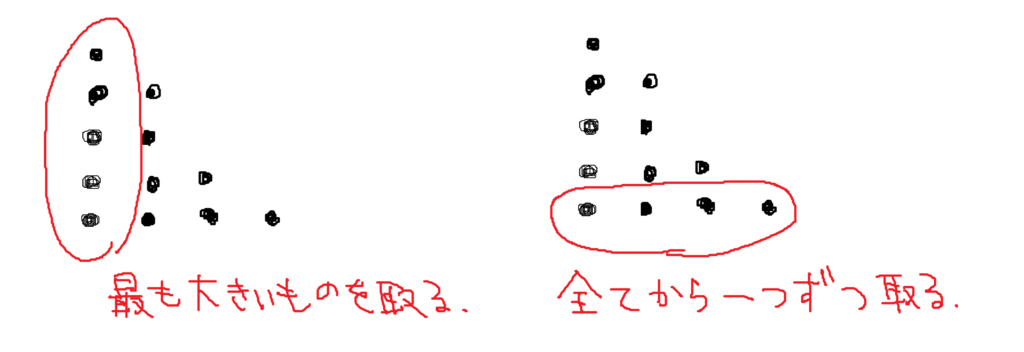
- キャンディが最も多く残っている山をひとつ選び、その山のキャンディをすべて食べる。
- キャンディが残っているすべての山から、1 個ずつキャンディを食べる。
これは、各列にキャンディーの山の個数分だけ丸を並べた図形で考えると、行と列の削除に対応しています。これが効率的な解法に至る重要な考察になっています。
分割数
自然数 \(n\) を自然数の非減少数列 \(x_i\) を用いて \(n= \sum x_i\) と表すことを整分割といい、その分け方の個数を分割数といいます。例えば、\begin{align} 5=&1+1+1+1+1 \\ =& 2+1+1+1 \\ =& 3+1+1 \\ =& 4 + 1 \\ =& 2+2+1 \\ =& 3 + 2 \\ =&5\end{align} なので、\(5\) の分割数は \(7\) です。分割数の性質は、フェーラズ図形という整分割の可視化により導かれることがあります。分割後のそれぞれの数の分だけドットを上の行から並べた図形です。例えば、\(12=5+4+2+1\) のときは下のようになります。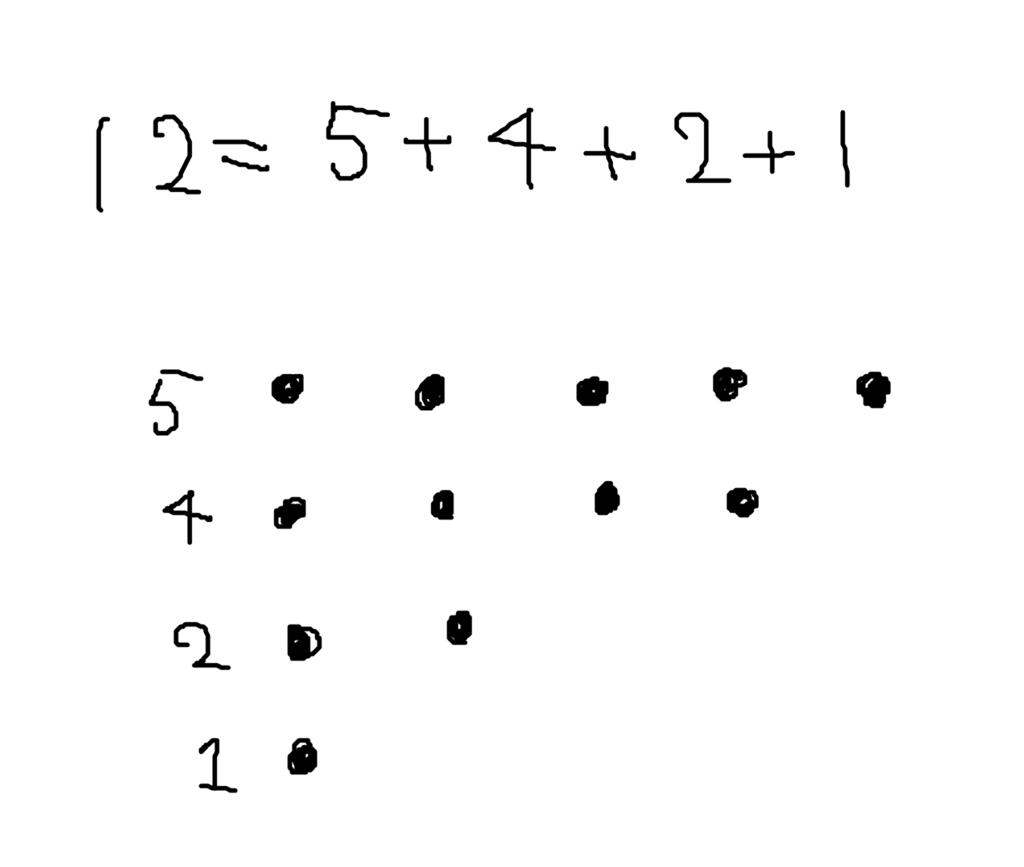
一方、列方向から見ても \(12\) になっており、\(12=4+3+2+2+1\) です（共役）。このことから、最大値が \(k\) の \(n\) の分割の個数と、\(k\) 個への \(n\) の分割の個数は等しいことが分かります。このほかにも、
- オイラーの五角数定理・ヤコビの三重積
- \(m,l\) を奇数とする。各数が \(m\) 以下の偶数で、項数が \(l\) 個以下の分割の総数と、各数が \(m\) 以下の奇数、項数が \(l\) 個以下の分割の総数が等しい。
- 共役が自分自身と等しい \(n\) の分割の総数と相異なる奇数への \(n\) の分割の総数が等しい。
のような事実をフェラーズ図形で示せます。
Comments