まとめ中………

\(a[i] = g[i] \oplus \bigoplus_{j=s[i]}^{t[i]} b[j]\)
b[j] は a[1:j] から計算された元、\(\oplus\) はモノイドの演算。セグメント木に載せる。定数個連ねた\(a[i] = g[i] \oplus \bigoplus_k\bigoplus_{j=s_k[i]}^{t_k[i]} b_k[j]\) のような形もある。
項の依存関係はDAGで表せる。すでに計算した項についてだけ、積を取るという条件が出てくるが、これは、全ての項を予め単位元で初期化しておくことで無視できる。例えば下の例では min の範囲の条件 \(j < i\) は全ての項を \(\infty\) で初期化することにより無視できる。
\begin{align}
a[i] &= \min_{g[j] < g[i], j < i}(a[j] + f_1[i] + f_2[j]) \\
&= f_1[i]+\min_{g[j] < g[i]}b[j]
\end{align}
区間和の場合は O(1)
\begin{align}
a[i] &= \sum_{j=s[i]}^{t[i]} a[j] \\
&= b[t[i]]-b[s[i]-1]
\end{align}

区間DP

区間dpは区間の小さい順に更新していく。2次元平面に図示すると更新順序は下のようになる。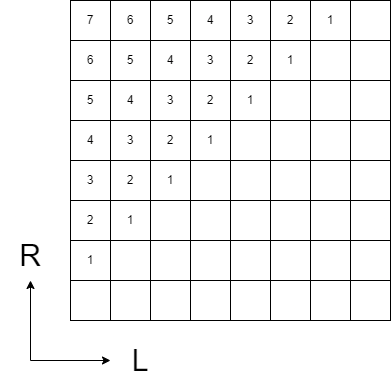 

\begin{align}
dp[i][j]= \max_{0 \leq d \leq w} dp[i+d][j-w+d] + f(i+d)+g(j-w+d)
\end{align}(ABC303)

足し算の畳み込み

\begin{align}
a[l][r] &= \sum_{\substack{l < s < r,\\ g[l] < g[s] < g[r]}} \left(a[l][s] + a[s][r]\right)\\
&= \sum_{g[l] < g[s] < g[r]} a[l][s] + \sum_{g[l] < g[s] < g[r]} a[s][r]\\
&= \sum_{g[l] < g[s] < g[r]} b_l[s] + \sum_{g[l] < g[s] < g[r]} c_r[s]\\
\end{align}
BITを使うと \(O(n^2 \log n)\) になる（ARC108E）。分配法則が成り立たない演算（例えばminや掛け算）だと畳み込みの部分が分けられない。

min plus の畳み込み (Monge)

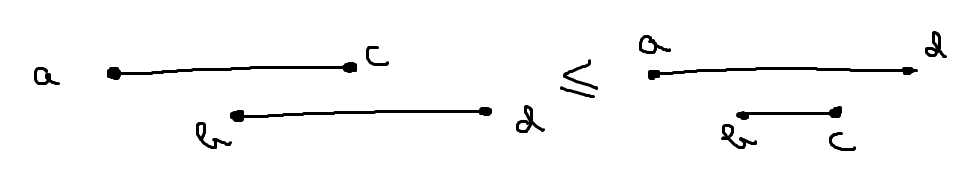
\(w_{i, j}\) が Monge かつ 単調非減少関数 (\([i, j] \subset [k, l]\) ならば \(w_{i, j} \leq w_{k, l}\)) のとき $$dp[i][j]=\min_{i < s < j}(dp[i][s]+dp[s][j]) + w_{i,j}$$ は Mongeで \(O(n^2)\) になる(ref)。

\(a \leq b\) とする。f が区間上のMongeのとき、優モジュラと同様にして、区間が大きいほど、f の微分も大きくなる。ここから dp がMongeになる。従って、\(g(a, b) = \mathrm{argmin}_s ( f(a, s) + f(s, b))\) と置くと \(g(a, b-1) \leq g(a, b) \leq g(a+1, b)\). 　すると、$$g(0, d-1) \leq g(0, d) \leq g(1, d) \leq g(1, d+1) \leq g(2,d+1)\leq g(2, d+2) \leq \cdots$$となるので\(O(n^2)\) となる。

Monge

\(f\) が集合上の優モジュラ関数ならば \(g(L, R):=f([L, R])\) はMongeになる。例えば、
\(A_{i,j} = \min_{i \leq k \leq j} a_k\) は Monge（ARC067F）。優モジュラ関数の定義
\begin{align}
&\forall S, \forall T, f(S \cap T) + f(S \cup T) \geq f(S) + f(T) \\
\Leftrightarrow & \forall A, \forall c, \forall d, f(A \cup c \cup d) – f(A \cup c) \geq f(A\cup d) – f(A)
\end{align}
より \(f\) （負も取る）は集合が大きいほど加速的に大きくなる。

整数の積の分割のDP

整数から半環への写像 \(g\) について、積の分割の和を取って $$f(n, k) = \sum_{\prod \lambda_i = n, \lambda_i \leq \lambda_{i+1}, \lambda_i \leq k} \prod_{i} g(\lambda_i)$$ と置くと、$$f(n, k) = f(n,k-1)+g(k)f(n/k,k)$$ が成り立つ。\(n, k \leq N\) について \(O(N \log N)\) で列挙できる（CF1699E）。

凸関数の和

\(x_1 \leq x_2 \leq \cdots \leq x_n\) の下、\(\min \sum f_i(x_i)\) を求めよ。ただし、\(f_i(x)\) は凸関数である(yuki2009)。\(f_i(x)\) が最小となる \(x\) を \(\omega_i\) とする。\(\frac{d}{dx} f_i,\frac{d}{dx} f_j \) の符号が互いに相異なるのは、区間 \([\omega_i, \omega_j]\) (\(\omega_i < \omega_j\)) だけである。\(\omega_{i} > \omega_{i+1}\) ならば、\(x_i = x_{i+1}\) としてもよい。凸関数の和は凸関数であるから、\(n\)が一つ小さい問題に帰着できた。\(\omega_1 \leq \omega_{2} \leq \cdots \leq \omega_n\) ならば \(x_i = \omega_i\) とするのが最適。

CHT

\begin{align}
dp[i]=&\min (dp[j]+(a_i-a_j)^2)\\
=&a_i^2+\min (f[j]-2a_ia_j)
\end{align}

ただし \(f[j]=dp[j]+a_j^2\)。

$$dp[i]=\min(dp[i-1],\min_j dp[j-1] + \sum_{k=i}^j a_k + (i-j)(i-j+1)/2)$$　(ABC066F)

区間\([j,i]\)に対して重み \(f[j]+g[i]+x[i]y[j]\) を割り当てる。\([1,n]\)から disjoint ないくつかの区間を取るときの最大重み。左からDPすると$$dp[i] = \max\left(dp[i-1], g[i]+\max_j \left(dp[j-1]+f[j]+x[j]y[i]\right)\right)$$という漸化式が得られる。右からDPしても同様の式が得られる。

各 \(i\) について \(i\) を含む区間が存在する場合/しない場合の最大重みを求めたい。存在しない場合は prefix dp と suffix dp を組み合わせればよい。存在する場合を考える。\(M\) と \(i\) (\(i > M\)) が同じ区間に含まれる場合の最大重みは
$$dp[i] = \max\left(dp[i-1], g[i]+\max_{j \leq M} \left(dp[j-1]+f[j]+x[j]y[i]\right)\right)$$ によって計算できる。また、\(i\) と \(M\) が同じ区間に含まれない場合の最大重みは、\((M,n]\) について同様の問題を解けばよい。よって、\(O(n \log(n)^2)\) で計算できる。

数列 \(s\) をいくつかの連続部分列に分割したときの \(\sum \max(s[a_i..a_{i+1}))-\min(s[a_i..a_{i+1}))\) の最大値を求めよ（CodeQUEEN2023）。\(-1,0,1\) からなり、prefix 和が 0 以上 1 以下の数列 \(b\) に対して \(\max b_is_i\) を求めればよい。