今の所、過去問並べただけ。
目次
後退解析
次(Next)の手番が勝つとき \(\mathcal{N}\), 前(Previous)の手番が勝つとき \(\mathcal{P}\), 引き分けのとき \(\mathcal{D}\) と書く。非不偏ゲームの遷移は、各ゲームを頂点とする有向グラフ \(G\) で表すことができる。勝敗は \(v \in V(G)\) について
- \(v\) が \(\mathcal{P}\) のとき、任意の \(v’ \in v\) は \(\mathcal{N}\)
- \(v\) について、任意の \(v’ \in v\) が \(\mathcal{N}\) のとき、\(v\) は \(\mathcal{P}\)
である。\(\mathcal{P}\) であることが確定している頂点から順に決定すればよい。勝敗の確定しなかった頂点は勝敗の確定しなかった頂点に遷移するのが最適である。従って、永遠に勝敗が決まらず、\(\mathcal{D}\) である。
generalized Sprague Grundy Theorem
loopのないゲームを finite rank, loopのあるゲームを infinite rankと呼ぶ。finite rankたちについては、先後最善を尽くしたときの終局までの手数をrankとする。有向グラフ \(G, H\) で表される二つのゲームの和は、有向グラフ \(G \times H\) で表せる。
ニム数が未確定の頂点は、暫定的にニム数を \(\infty\) として、帰納的にニム数を計算していく。\(m = \mathrm{mex}_{v’ \in v}(\mathcal G(v’))\) とする。任意の \(v’ \in v\) について \(\mathcal{G}(v’) > m\) ならば有限回で打ち消し可能な選択肢であることが分かっているとき、\(\mathcal{G}(v) = m\) としていく。すなわち、その時点で \(\mathcal{G}(v”) = m\) である \(v” \in v’\) が存在するならばよい。それ以上更新ができなくなったところで、ニム数が \(\infty\) である頂点 \(v\) は \(\mathcal{G}(v) = \infty(\{\mathcal{G}(v’) : \text{$v’ \in v$, $\mathrm{rank}(v’)$ is finite}\})\) とする。\(\infty\)のゲームからは必ず\(\infty\)のゲームに遷移できるが、ゲームの値に影響しないので \(\{\cdot\}\) には含めない。
- \(\mathcal{G}(v) = 0\) \(\Leftrightarrow\) \(v\) は \(\mathcal{P}\) 局面
- \(\mathcal{G}(v)\) が正整数ならば \(v\) は \(\mathcal{N}\) 局面
- \(\mathcal{G}(v) = \infty(\mathcal{A})\) で \(0 \in \mathcal{A}\) ならば、\(v\) は \(\mathcal{N}\) 局面
- \(\mathcal{G}(v) = \infty(\mathcal{A})\) で \(0 \not\in \mathcal{A}\) ならば、\(v\) は \(\mathcal{D}\) 局面
ゲームの和のニム数は
$$\mathcal{G}(u + v) = \mathcal{G}(u) \oplus \mathcal{G}(v)$$となる。ただし、\(\infty(\mathcal{A})\oplus \infty(\mathcal B) = \infty(\emptyset), \infty(\mathcal{A})\oplus b = \infty(\mathcal{A}\oplus b) = \infty(\{a \oplus b : a \in \mathcal{A}\})\) とする。\(\mathrm{rank}(u) = \infty\) ならば \(v\) に関わらず \(\mathrm{rank}(u+v) = \infty\) であることを用いた。この事実の証明:\(a,b\in\mathbb{N}\)について\(\infty(\mathcal{A})\oplus a = b\)ならば\(\infty(\mathcal{A})=a\oplus b\)なので矛盾。\(\infty(\mathcal{A})\oplus \infty(\mathcal{B})\) が rank最小のfinite rank とすると、u’+v, u+v’がfinite rankよりu’,v’がinfinite rankだが、rankが減少する遷移先が必ずあり、rankの最小性に反する。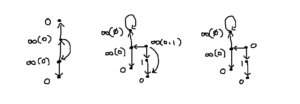
非不偏ゲームで A から B の遷移があり、A の帰結類を求める場合、A の選択肢と B の選択肢の共通部分に \(\mathcal{P}\) がある場合とそうでない場合で場合分けができる。前者の場合、A は \(\mathcal{N}\) である。後者の場合は、共通部分を全て存在しないものとしてゲームを解析できる。
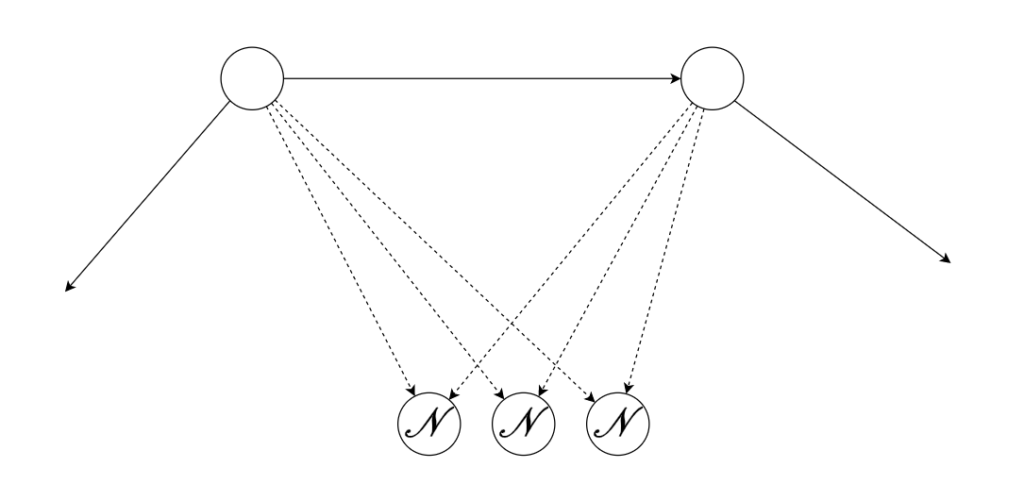
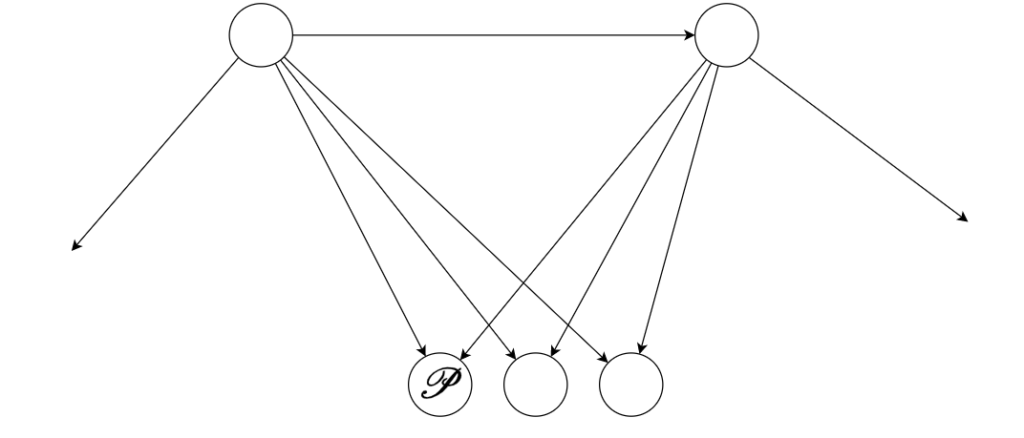
\(\mathcal P\) に接続する頂点は全て \(\mathcal N\) である。例えば Wythoff’s game で同じx座標の \(\mathcal P\) 局面が二つ以上ないのはこの事実からすぐに分かる。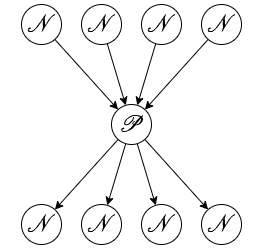
ニム数 \(n\) の頂点が存在する最小のグラフは \(K^{n+1}\) を頂点番号の小さい方から大きい方へ向きづけたグラフである。従って、辺は少なくとも \(\Theta(n^2)\) 個必要である。ニム数は、ゲームの誕生日の順に頂点を貪欲に彩色したときの色数に等しい。
DAGの後退解析
DAGの場合、後退解析は簡略化できる。閉路が存在しないので、勝敗が決まらない頂点は存在しない。
- ゲームの終了状態に、勝敗を割り振る。
- 勝敗が未確定の頂点を、一時的に、負け状態と仮定する。
- トポロジカル順序の逆順に頂点 \(v\) を見る。
- \(v\) が勝ちなら何もしない。\(v\) が負けなら、\(v\) に遷移可能な頂点を勝ちにする。
トポロジカル順序が自明ならば、手で勝敗が簡単に書き下せる場合がある。
DAGの後退解析をすればよい。先手の敗北条件は \(N = 0 \pmod {K+1} \) である。
DAGの後退解析。
DAGの後退解析。「直前に相手が \(x\) 個取り除いてなければ」勝ちという条件を論理和で配るので、各頂点の状態は
- 負け
- 直前に相手が \(x\) 個取り除いなければ、勝ち
- 直前に相手が何個取り除いていようが、勝ち
のいずれか。1つ目の状態が最短でも \(K+1\) 個おきにしか起きないので、更新回数は全体で \(O(N)\) になる。
- 駒を辺に沿って動かす。
- ゲームを終了する。
のどちらかを選ぶ。十分長いターンが経ってもまだゲームが終了していないときは、後手の手番後に強制終了する。ゲームが終了したときに、駒が置いてある頂点の数字を先手は最大化、後手は最小化したい。数字はいくつになるか。(ARC038D)
スコアについて二分探索すると後退解析になる。
いくつかの根付き木が与えられる。交互に次のいずれかの操作を繰り返す。
- 1ターン目ならば駒を好きな木の根に置く。
- 葉でなければ、駒を子に移動する
- 葉であれば、まだ選ばれていない木の根に駒を移動する
操作できなくなったほうが負け。どちらが勝つか。
(Kupc2019E)
木の根を選び、葉まで駒を動かしてから、次の根を選ぶのが先手後手のどちらになっているか考える。
- 先手の意思で、先手後手を入れ替えることができる
- 先手の意思で、先手後手をそのままにすることができる
(True, True) を選ぶと先手の勝ち。(False, False) を選ぶと後手の勝ち。従って (False, False) が選ばれるのは最後。(True, False) ならば先手後手は必ず入れ替わる。(False, True) ならば先手後手は必ずそのまま。従って、(False, True) は勝敗と無関係。
勝敗の単調性
あるパラメータ A が大きいほど先手が有利ならば、
- \(f_1(S, a) :=\) 状態 S でパラメータ A = a のときの勝敗
を持つ dp から
- \(f_2(S) :=\) 状態 S のとき、先手が勝つための A の最小値
を持つ dp に変更でき、状態数が減らせる。
N 個の石が相異なる非負整数座標 \(x_1, x_2, \ldots, x_N\) (\(0 < x_1 \leq \cdots < x_N\)) に置かれている。交互に、最も大きい座標に置かれている石を、他の石と重ならないように、より小さい非負整数座標に置き換える。どちらが勝つか。
(ARC137C)
単調性より、\(x_N\) が大きいほど先手が有利。戦略盗みにより、\(x_N-x_{N-1} \geq 2\) ならば先手の勝ち。さもなくば、\(x_N-x_{N-1} =1\) を保ちながら遷移するしかないので、最適手は \(O(N)\) でシミュレートできる。
- 先手は好きな頂点を1つ選び書き込まれた数字を零にする。
- 後手は子に駒を移動する。葉に移動した場合はゲーム終了。葉でもなくとも、後手の意思で終了にできる。
ゲーム終了時点で駒がある頂点に書き込まれた数字が得点になる。先手は得点を最小化、後手は得点を最大化したい。何点になるか。(ABC246G)
得点はX点以上か?について二分探索して、後退解析。取り除ける頂点が多いほど先手は有利なので、dp[v] := (頂点 v の部分木でゲームをしたとき得点を X 未満にするには、予め何個の頂点の得点を零にしておく必要があるか) について dp ができる。
\(a_1, a_2, \ldots, a_N\) 個の石からなる山が \(N\) 個ある。Aさんは右端の山から好きな個数の石を取ることができ、Bさんは左端の山から好きな個数の石を取ることができる。交互に操作を行う。どちらが勝つか。
(AGC048D)
指せる手の単調性より
- \(a_1\) が大きいほど A さんが有利
- \(a_N\) が大きいほど B さんが有利
だから、操作は
- 山から石を一つだけ取る
- 山から石を全て取る
のどちらかであるとしても勝敗は変化しない。
- 残っている山が \(l, \ldots, r\) 番目で、\(l\) 番目の山以外は初期状態と石の個数が同じである。A さん先手で、A さんの勝ちとなる \(a_l\) の最小値 \(f(l, r)\)
- 残っている山が \(l, \ldots, r\) 番目で、\(r\) 番目の山以外は初期状態と石の個数が同じである。B さん先手で、B さんの勝ちとなる \(a_r\) の最小値 \(g(l, r)\)
\(f(l, r-1), g(l+1, r)\) から \(f(l, r), g(l, r)\) が \(O(1)\) で求まる。
不変量に着目する
二部グラフ
二部グラフ上のゲームの場合、各部集合が何らかの不変量と関連していることが多い。特に、グリッドグラフが頻出である。
- \((x+y) \bmod 2 = 0\) に置かれた駒の個数 A
- \((x+y) \bmod 2 = 1\) に置かれた駒の個数 B
と置く。(A, B) の勝敗を2次元平面にプロットすると、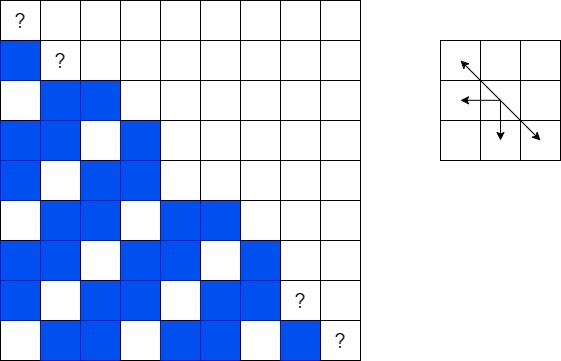 のようになる。青マスが勝ち。端のはてなのマスは、はてな同士を行き来することで勝敗が決まらないように思えるが、最終的に \(x = y\) 方向に移動せざるを得なくなることから、外側のはてなの方が勝ちになる。よって、\(A-B = 0 \pmod 3 \Leftrightarrow \) 後手勝ち。N次元に拡張できる。
のようになる。青マスが勝ち。端のはてなのマスは、はてな同士を行き来することで勝敗が決まらないように思えるが、最終的に \(x = y\) 方向に移動せざるを得なくなることから、外側のはてなの方が勝ちになる。よって、\(A-B = 0 \pmod 3 \Leftrightarrow \) 後手勝ち。N次元に拡張できる。
- s, t の点連結度が1のとき先手の勝ち。
- s, t の点連結度が2のとき、点連結度を1にしたほうが負けなので、その直前では、2つの内素な s-t パスだけになる。二部グラフなので、このときの頂点数はそれまでの操作によらない。従って勝敗も O(1) で分かる。
グリッドグラフ
上手くマッチングを作る。
偶奇
偶奇が不変量に関連していることがある。
- すべての要素を 1 減らす。全ての要素が正整数である場合のみこの操作ができる。
- 正整数を一つ選び、1 減らす。
操作ができなくなった方が負け。どちらが勝つか O(1) で求めよ。
(KUPC2020春E)
Nが奇数の時は、どちらの操作でも総和の偶奇が変化するので簡単。Nが偶数のときは、最小値, 総和が両方偶数 ⇔ 後手勝ち。
gcd で割らなければ、\(\sum (A_i-1)\) 回操作ができる。A の要素に奇数が含まれていれば gcd は奇数で、\(A_i, A_i/\mathrm{gcd}(A)\) の偶奇は同じ。従って、\(\sum (A_i-1)\) が不変。A の要素に奇数が一つ以上含まれていれば、奇数を二つ以上にして相手に渡せる。従って、 gcd(A) = 1 より奇数は必ず含まれているので \(\sum (A_i-1) = 1 \pmod 2\) ならば先手の勝ち。A に奇数が一つだけ含まれていて、\(\sum (A_i-1) = 0 \pmod 2\) ならば、その奇数から 1 引いて gcd で割ってから相手に渡すことになる。このような操作は \(O(\log(\max(A))\) 回しか行われない。
- 山を2つに分割する。
- 各山から石を一つ取り除く。ただし、各山に2つ以上の石がなくてはならない。
どちらが勝つか。(yukicoder1852)
(i) : \(\min(a)=1\) のとき、 \(S := \sum (a_i-1)=1 \Leftrightarrow \) 先手の勝ち。
(ii) : \(\min(a) > 1\) のとき、\(a_1\) を \(1, a_1-1\) に分割すると、(i) の \(S \leftarrow S-1\) の場合に帰着される。従って、\(S\) が奇数なら先手の勝ち。さもなくば、\(\forall i, a_i \leftarrow a_i-1\) の操作しか先手はできず、後手に \(S \leftarrow S-N\) の状態で渡される。\(N\) が奇数なら、先手の負け。\(N\) が偶数なら、\(\min(a)\) の偶奇で勝敗が決する。
連結になる直前の連結成分の大きさが \(k, n-k\) とすると、追加された辺の本数は \(n(n-1)/2-|E|-k(n-k)\) である。従って \(k(n-k)\) の偶奇によって勝敗が決まることが分かる。\(n\) が奇数ならば、\(k(n-k) \bmod 2\) は \(k\) に依らず決定する。従って、以降は \(n\) が偶数の場合のみを考える。先手は、偶成分が2つの状態を作ると勝ち、あるいは、奇成分が2つの状態を作ると勝ちのどちらかに排反でなる。次の三つの数をパラメータにして考察する。
- 偶成分の個数
- 奇成分の個数
- 連結成分の個数を変えずに追加できる辺の個数の偶奇
この三つの数は、各操作によって次のように変化する。
- 偶成分と偶成分をマージ \((-1, 0, 1)\)
- 偶成分と奇成分をマージ \((0, -1, 1)\)
- 奇成分と奇成分をマージ \((1, -2, 0)\)
- 連結成分内で辺を追加 \((0, 0, 1)\)
ところで$$(-1, 0, 1) + (1, -2, 0) = (0, -2, 1)$$だから
偶成分2つより、奇成分2つの方が作りにくい。先手が偶成分2つの状態を作りたいとする。奇成分は常に偶数個あるから、偶成分が一つでもある状態で回ってこれば、偶成分が2つ以上にして相手に渡せる。相手は偶成分を高々一つしか減らせないので、これは勝ちである。奇成分しかない場合を考える。相手に偶成分を作ってもらうために、奇成分のみの状態で手番を相手に渡す必要がある。つまり、連結成分内の辺の追加で手番を入れ替えなければならない。頑張って場合分け。
グラフGが与えられる。偶点を交互に取り除く。行動できなくなったほうが負け。どちらが勝つか。
\(\sum_v d(v) = 2|E|\) より奇点は偶数個あるのでNの偶奇で勝敗が決まる。
グラフ理論
後手が勝つならば、先手はその戦略を採用することで、先後どちらも2つの全域木が取れる。逆にこの時、後手が勝てることは、木がマトロイドであることと基交換定理から従う。Nash-Williamsの定理より、2個の辺素な全域木が取れる⇔任意の頂点集合の分割Pについて、Pのcross edgeの個数が \(2(|P|-1)\) 以上。全域木が取れないのなら、cross edgeの個数が2(|P|-1)未満の分割がある。このcross edgeを先手は取ると後手の勝ちを阻止できる。辺素な全域木を取るアルゴリズム
先手が全域木に含まれる辺を選んだ時、その辺でほかの全域木にできる基本サイクルを壊すように後手が辺を選べばよい。
Nim
一山崩し
\(\mathrm{sub}(S)\) あるいは \(\mathrm{sub}(s_1, s_2, \ldots, s_n)\)
と書くことにする。また、\(S\) が有限集合の時、\(\mathrm{allbut}(S)=\mathrm{sub}(\mathbb{N} \setminus S)\) と書く。
\(\forall x \in S, \exists y ∈ S, x + y = C\) ならば周期 \(C\) と分かる。また、\(\{1, 2, \ldots, k\} \subseteq S\) かつ \(\forall x ∈ S \setminus \{1, 2, \ldots, k\}, (k + 1) | x\) ならば、\(N = 0 \pmod {k + 1}\) ⇔ 後手勝ち である。
\(\#S \leq 2\) の時の勝敗は?
\(S = \{a, b\}\) と置く。\(a < b\) としてよい。\(N \leftarrow N \bmod {(a+b)}\) としても勝敗は変わらない。\(N < b\) かつ \(\lfloor N/a \rfloor =1 \pmod 2\) または \(b \leq N < a + b\) のとき先手勝ち。
\(S = \{s_1, s_2, \ldots, s_n\}_{<}\) とする。\(s_{i+1} \leq s_i + s_1\) とするとニム列は \(0^{s_1}1^{s_2-s_1}2^{s_3-s_2-s_1} \cdots\) のようになって、周期はある \(i\) を用いて \(s_1+s_i\) となる。
\(\mathrm{sub}(S)\) のニム列が純周期的で周期 \(p\) のとき、\(\mathrm{sub}(S\cup \{mp\}) \) \((m \geq 0)\) と同じニム列を持つ。
ある \(n_0, a\) が存在して、任意の \(n \geq n_0\) について \(\mathcal{G}(n)=\mathcal{G}(n+a)\) であるとき、周期的という。ある \(n_0, a, b\) が存在して、任意の \(n \geq n_0\) について \(\mathcal{G}(n)+b=\mathcal{G}(n+a)\) であるとき、算術周期的という。sub のニムは周期的、allbut のニムは算術周期的になる。\(\mathrm{sub}(S)\) について \(\mathcal{G}(n)\) は \(f(n)=(\mathcal{G}(n-1), \mathcal{G}(n-2), \ldots, \mathcal{G}(n-\max(S)))\) のみから決まる。\(\max\mathcal{G}(n) \leq |S|\) なので\(f(n)=f(m)\) となる \(n,m\) が存在する。従って周期的。\(\mathrm{allbut}(S)\)について, 暫定的に全ての\(n\)について\(\mathcal{G}(n)=\infty\)としてニムを値の昇順に埋める。\(k\) 未満のニムが全て定まったとする。\(\mathcal{G}(n) = \infty\) となる最小の \(n\) を取り、\(\mathcal{G}(n)=k\) とする。ニム\(k\)への遷移が不可能なものを順にニム\(k\)で確定していく。このようなアルゴリズムから、\(k\) 以上のニムは、\(\{i : \mathcal{G}(i) < k, i \geq n\}\) のみで定まる。この集合が有限個しかないので算術周期的(Sleator)
\(2s_n < b\) のとき \(G=\mathrm{allbut}(s_1, s_2, \ldots, s_n)\) と \(H=\mathrm{allbut}(s_1, s_2, \ldots, s_n, b)\) のニム列は等しい。
帰納法で示す。\(n < b\) ならば明らかに\(\mathcal{G}_H(n)=\mathcal{G}_G(n)\) である。\(n < k\) で成り立つとする。\(\mathcal{G}_G(k) \neq \mathcal{G}_H(k)\) ならば \(\mathcal{G}_H(n-b) = g_H(n)\) である。
帰納法の仮定より
\begin{align}
\mathcal{G}_G(n-b) \leq \mathcal{G}_G(n-b+s) \\
\Leftrightarrow \mathcal{G}_H(n-b) \leq \mathcal{G}_H(n-b+s) \\
\end{align}
である。
\(n-b < n-b+s_n < n-s_n\) より \(n-b+s_n\) は \(H\) の選択肢であるから、\(\mathcal{G}_H(n-b) < \mathcal{G}_H(n-b+s)\) であるが、これは \(x \neq n-b, x < n-s_n\) で \(\mathcal{G}_H(x) = \mathcal{G}_H(n-b)\) の存在をしているので矛盾。
\(ax+by > 0\) となる格子点の集合 \(U\) を考える。sub(a, b) は \(N = ax + by\) となる格子点 \((x, y)\) から格子点 \((x-1, y), (x, y-1) \in U\) のどちらかに移動を繰り返すゲームだともいえる(ARC144F)。
\(0 < a \leq m /2\) の場合:順に計算することで \(0 \leq i < a\),\(0 \leq j\), について\begin{align} \mathcal{G}(i) &= 0 \\ \mathcal{G}(i + a + mj) &\neq 0 \\ \mathcal{G}(i + 2a + mj) &= 0 \\ \mathcal{G}(i + 3a + mj) &= 1 \\ \mathcal{G}(i + 4a + mj) &= 0 \\ \vdots & \\ \mathcal{G}(i + ka+mj) &= \delta_{k \bmod 2, 0} \end{align}が得られる。ただし、\(k\) は \(i+ka \geq m \iff k \geq (m-i)/a\) を満たす最小の整数とする。\(i\) を固定して、\(G_q = (\mathcal{G}(i + qa+mj))_{j \geq 0}\) と置くと、\( \delta_{k \bmod 2,0}=0\) のときは \(G_0=(0,0,\ldots), G_1 = (1,1,\ldots)\)、\(\delta_{k \bmod 2,0}=1\) のときは \(G_0=(0,1,1,1,\ldots)\), \(G_1 = (1,2,2,2,\dots)\) となる。
\(m/2 < a < m\) の場合:順に計算することで \(0 \leq j\) について
\begin{align}
\mathcal{G}(i) &= 0 & (0 \leq i \lt a)\\
\mathcal{G}(i+a+mj) &\neq 0 & (0 \leq i \lt a)\\
\mathcal{G}(i+a+mj) &= 0 & (a \leq i < m)\end{align}
が得られる\(a \leq i < a + b\) のとき
\(a - b\leq i + a - m < a\) である。
よって、\(\mathcal{G}(i+mj) = 0\) for \(a-b \leq i < a\)である。
\(G_{k} = (\mathcal{G}(i-bk+mj)_{j \geq 0})\) と置くと \(G_{0} = (0,0,\ldots,), G_{1}=(0,1,1,1),G_{2}=(0,1,2,2,\ldots)\) となり、\(i - bk \geq 0\) で成立。
\(\mathcal{G}(i+mj)\) for \(a \leq i\) については、\(\mathcal{G}(i+mj) = 1 + \mathcal{G}(i-a+mj)\)。
(m,a)=(35, 30)としてG(ah+mw)を(h,w)にプロット(code)
xxxxxxxxxxxxxxxxxxx01222222222222222222222222222
xxxxxxxxxxxxxxxxxx01233333333333333333333333333
xxxxxxxxxxxxxxxxx01234444444444444444444444444
xxxxxxxxxxxxxxxx01234555555555555555555555555
xxxxxxxxxxxxxxxx1234566666666666666666666666
xxxxxxxxxxxxxxx0000000000000000000000000000
xxxxxxxxxxxxxx0111111111111111111111111111
xxxxxxxxxxxxx01222222222222222222222222222
xxxxxxxxxxxx01233333333333333333333333333
xxxxxxxxxxx01234444444444444444444444444
xxxxxxxxxx01234555555555555555555555555
xxxxxxxxxx1234566666666666666666666666
xxxxxxxxx0000000000000000000000000000
xxxxxxxx0111111111111111111111111111
xxxxxxx01222222222222222222222222222
xxxxxx01233333333333333333333333333
xxxxx01234444444444444444444444444
xxxx01234555555555555555555555555
xxxx1234566666666666666666666666
xxx0000000000000000000000000000
xx0111111111111111111111111111
x01222222222222222222222222222
二山崩し
Allen):\(H_1=1, H_{i+1} = H_i + \min_{j \leq i} \{H_j : f(H_j) \geq H_i\}\) によって定義される数列 \(H\) の項で \(n\) が表せることとと \(\mathcal{P}\) が同値(\(f(H_i) < H_i\) となる \(H_i\) が末尾)。任意の非負整数 \(n\) が \(n=\sum_i H_{j_i}\) かつ (\(f(H_{j_i}) < H_{j_{i+1}}\) for all i) として一意に表せて、必勝側はLSBを引けばよい。
\begin{align}
&H_{j_1} + H_{j_2} + \cdots + H_{j_n} \\
< &H_{j_2+1} + H_{j_3} + \cdots H_{j_n} \\
\leq &H_{j_3+1}+H_{j_4}+\cdots H_{j_n}\\
\vdots\\
\leq&H_{j_n+1}
\end{align}
よって、貪欲に大きい方から取ることで一意な表示になる。またここから、\(H_a – H_b\) (\(a > b\)) の LSB \(H_c\) は \(f(H_b) \geq H_c\) を満たし、必勝側の戦略が実行可能である。Michaelではこのような分解を用いない方法が取られている。
\((x,y)\) が \(\mathcal{P}\) ならば \((x+i, y),(x,y+i),(x+i,y+i)\) は \(\mathcal{N}\). 遷移をマス目上に書いてみると、\begin{align} x_i &= \mathrm{mex}\{x_j, y_j\}\\ y_i &= x_i + i\end{align} によって定まる山 \((x_i, y_i), (y_i, x_i)\) が負けであることが分かる。
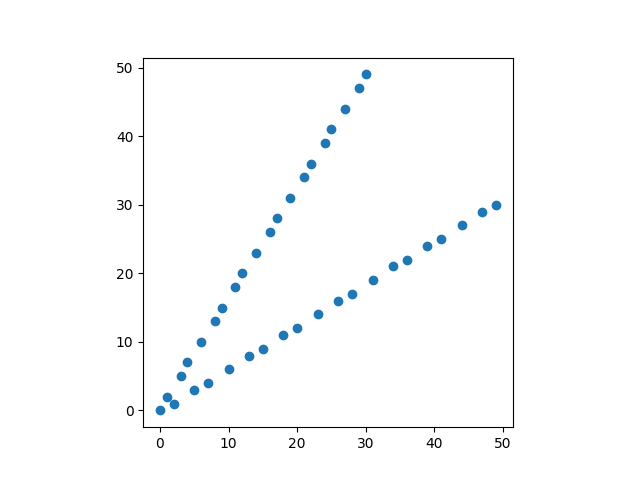
レイリーの定理:\(\alpha, \beta\) が無理数で \(1 / \alpha + 1 / \beta = 1\) ならば \(\{ \lfloor i\alpha \rfloor : i \in \mathbb{N}\}, \{\lfloor i\beta \rfloor : i \in \mathbb{N}\}\) は \(\mathbb N\) の分割である。
(証明)無理数 \(\alpha, \beta\) が \(1 / \alpha + 1 / \beta = 1\) を満たすとする。\(A := \{i\alpha : i \in \mathbb{N}\}, B := \{i\beta : i \in \mathbb{N}\}\) と置く。\(i \alpha = j \beta \Leftrightarrow \alpha / \beta = j / i\) は、左辺 \(\alpha / \beta = \alpha-1\) が無理数、右辺 \(j/i\) が有理数なので、起こりえない。従って、\(A, B\) は交わらない。\(f(x) = \#\{y \in A \cup B : y \leq x\}\) とすると、\(f:A\cup B \rightarrow \mathbb{N}\) の全単射である。\(j\beta \leq i\alpha\) を満たす \(j\) の個数は \(\lfloor i\alpha / \beta\rfloor = \lfloor i(\alpha-1)\rfloor\) なので \(f(i\alpha) = \lfloor i \alpha \rfloor, f(i\beta) = \lfloor i\beta \rfloor \). 従って \(\{\lfloor i \alpha \rfloor : i \in \mathbb{N}\}\) と \(\{\lfloor i \beta \rfloor : i \in \mathbb{N}\}\) は相補的である■
\(\mathbb{N}\) の分割 \(A = \{a_1, a_2, \ldots,\}_<, B = \{b_1, b_2, \ldots, \}_<\) が \(b_i = a_i + i, a_1 = 1\) を満たすならば、そのような数列は明らかに一通りしかなく、レイリーの定理はその表現を与える。黄金比 \(\phi\) は \(1 / \phi + 1 / \phi^2 = 1\) を満たし、\(x_i = \lfloor i\phi \rfloor, y_i = \lfloor i \phi^2\rfloor\) となる。確かに、\begin{align} & i + x_i = \lfloor i (\phi +1)\rfloor = \lfloor i \phi^2\rfloor = y_i \\ &\lfloor n\phi \rfloor = \mathrm{mex}\{\lfloor i\phi \rfloor, \lfloor i \phi^2 \rfloor : i < n\}\end{align} となっている。一方、フィボナッチ進法を使って、そのような集合を別の方法で表現することができる。\(x \leq y\) の先手負けの状態 \((x, y)\) のゼッケンドルフの表現は次の様になっている。
| i | x | y | i のゼッケンドルフの表現 | x のゼッケンドルフの表現 | y のゼッケンドルフの表現 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 00000000 | 00000000 | 000000000 |
| 1 | 1 | 2 | 00000010 | 00000010 | 000000100 |
| 2 | 3 | 5 | 00000100 | 00001000 | 000010000 |
| 3 | 4 | 7 | 00001000 | 00001010 | 000010100 |
| 4 | 6 | 10 | 00001010 | 00010010 | 000100100 |
| 5 | 8 | 13 | 00010000 | 00100000 | 001000000 |
| 6 | 9 | 15 | 00010010 | 00100010 | 001000100 |
| 7 | 11 | 18 | 00010100 | 00101000 | 001010000 |
| 8 | 12 | 20 | 00100000 | 00101010 | 001010100 |
| 9 | 14 | 23 | 00100010 | 01000010 | 010000100 |
| 10 | 16 | 26 | 00100100 | 01001000 | 010010000 |
| 11 | 17 | 28 | 00101000 | 01001010 | 010010100 |
\(\mathcal{P}\) ポジションは \((0, 0)\) または \((\overleftarrow{x}, x)\) の形をしている。また、\(x\) の正規ゼッケンドルフ表現の LSB は偶数の位置に、\(\overleftarrow{x}\) の LSB は奇数の位置にある。LSB の偶奇性と、\(\overleftarrow{x}, x\) は一方からもう一方が定まることから、\((\overleftarrow{x}-i,x), (\overleftarrow{x},x-i), \) は \(\mathcal{P}\) にならない。
\(x = \overrightarrow x + \overrightarrow{\overrightarrow{x}}\) なので、\begin{align}
& \overleftarrow x-x \\
={}& (y + \overrightarrow x)-x \\
={}& \overrightarrow{x}
\end{align}
である。\(\overrightarrow{x}\) は LSB が奇数の位置にあるゼッケンドルフ表現で表せる。各正整数 \(n\) に対して、このような表現はただ一つ存在し、第二正規ゼッケンドルフ表現と呼ぶ。第二正規ゼッケンドルフ表現は \(n-1\) の正規ゼッケンドルフ表現に \(1\) を足せば得られる。例えば、\(1010 + 1 = 10000\) である。一意性は、第二正規ゼッケンドルフ表現 \(1\) を引くと \(n-1\) の正規ゼッケンドルフ表現になり、正規ゼッケンドルフ表現が一意であることから従う。以上から、\((\overleftarrow x, x)\) が \(\mathcal P\) ならば \((\overleftarrow x-i, x-i)\) は \(\mathcal{P}\) でない。
\((y, x) \) (\(y \geq x\)) が \(\mathcal{N}\) だとする。(i) \(x\) の LSB が偶数の場合:\(y \geq \overleftarrow{x}\) ならば \((y-i, x)\) で \(\mathcal{P}\) に遷移できる。そうでないとする。\(\overrightarrow{d}:=y-x < \overleftarrow{x}-x\) なので、\((\overleftarrow d, d) = (y-i, x-i)\) となる \(i\) が存在して \(\mathcal{P}\) に遷移できる。ただし、\(\overrightarrow d\) は第二正規表現とする。(ii) \(x\) の LSB が奇数の場合:\(x\) のLSBは1番目にはならないことに注意。\(y \geq x \geq \overrightarrow {x}\) なので \((y-i, x)\) で \(\mathcal{P}\) に遷移できる。
\(F_0=F_1=1, F_{n}=F_{n-1}+F_{n-2}\) の母関数 \(f\) は
\begin{align}
f&=\sum_{i \geq 0} F_ix^i \\
&= \frac{1}{1-x-x^2} \\
&= \frac{1}{(1-\phi x)(1+\phi^{-1}x)}
\end{align}
\(\lfloor \phi x\rfloor \) のゼッケンドルフ表示を求める。\(\phi xf-f = -\frac{1}{1+\phi^{-1}x}\) と \(\phi^{-2} < \frac{1}{2}\) より \(-1< \phi x – \overleftarrow{x} < 1\) で \(x\) の LSB が (0-indexed) 奇数桁目のときは負、偶数桁目の時は正。従って、\(\lfloor \phi x\rfloor\) のゼッケンドルフ表示は、\(x\) のゼッケンドルフ表示を左シフトしたあと、LSBが (0-indexed) 偶数番目ならば \(1\) 引くことで得られる。\(\lfloor \phi^2 x\rfloor = x + \lfloor \phi x\rfloor\) は \(x\) が \(\lfloor \phi x\rfloor \) の右シフトになっていることに注意すると、\(\lfloor\phi^2x\rfloor\) は \(\lfloor \phi x\rfloor\) の左シフト。
\(k = \lfloor i \phi \rfloor \) と置くと、\(i\phi < k + 1 \Leftrightarrow i – 1/\phi < k\) なので \(\lfloor \lfloor i\phi \rfloor /\phi \rfloor = i – 1\) である。示すべき式は
\begin{align}
&k=\lfloor\lfloor i\phi^2 \rfloor/\phi\rfloor\\
\iff&k \leq \lfloor i\phi^2 \rfloor/\phi < k + 1 \\
\iff &k \leq (i+k )/\phi < k + 1\\
\iff &(\phi-1)k \leq i< (\phi-1)k + \phi\\
\iff &k/\phi \leq i< k/\phi + \phi\\
\end{align}
となる。左側の不等式は自明。右側の不等式は、 \(k \leq i \phi < k + 1\) より \(i < k/\phi + 1/\phi\) だから良い。それぞれのフィボナッチ進法を考えることで、ニム数が求まる。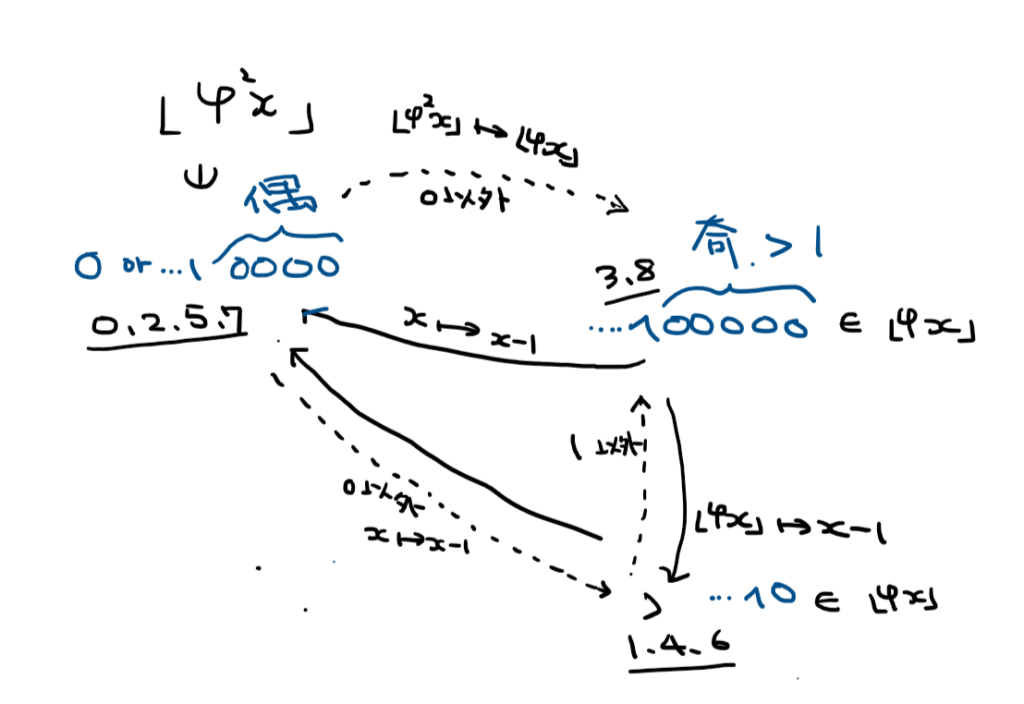
複数山崩し
真似っこ戦略により、\(x_i \leftarrow x_i \bmod (a+b)\) としても結果は変わらない。全ての要素が \(a\) 未満ならば先手の負け。さもなくば、先手は可能な限り多くの山から \(a\) 個ずつ石を取り去って、相手に渡す。このとき、\(b\) 個以上の山があれば後手の勝ち、さもなくば先手の勝ち。
非不偏ゲーム
左右のそれぞれが先手のときの勝敗を個別に分析する必要はない。
- 左右のうち、右が先手の時の勝敗が完全に分かっている。
- そのことから、左が先手のときの最善の一手目が得られる。
このとき、左が先手の時の勝敗が完全に得られる。(Xならば確実に勝つ/負ける)という条件が存在する方が条件が簡単になりやすく、そちらを主にして勝敗を分析するとよい。
Nを書いてはいけない。また、すでに書かれた数に対して、互いに素な数や、約数・倍数である数は書けない。どちらが勝つか。(Saint Petersburg 1997)
まずAは相異なる2つの素数の積 \(pq\) を書く。Bは \(p\) か \(q\) の倍数であって、\(pq\) の倍数でないものを書く。 \(pk\) を書いたとする。Aは常に続いて \(qk\) が書ける。従って先手の勝ち。N/pを書いた後、相手のkpに対して N/kを答える方法もある。
各行について、B は k 個のマスを選び、そのどれかを黒くすることができる。これは、A が書いたマスの行について、応手することでできる。各行 k 個のマスを非連結になるように選べるので、Aの負け。
\(5 \times 5\) のマスで、A, B は交互に白と黒の駒を置く。Aは白の駒が5個並んだ列・行・対角の何れかが作れると勝ち、さもなくば負けである。どちらが勝つか。
下のようなペアが作れるので後手の勝ち。
x626y
5ccd3
1bod1
5baa3
y424x
ペアリング。
書き込める場所が全てS..Sの形になると何を書き込んでもSO.かS.Sができて、相手がSOSを作れるので負け。負けるときは全てこのパターンである。先手は最初の二手で S..S の形を少なくとも一箇所作ることができ、マスの偶奇性も合わせると先手の勝ち。また、2i-1と2iをペアにして同じ文字を書くと後手は最低でも引き分けにできることが簡単に分かる。
\(n\) が偶数とする。偶数 \(n\) を持ったとき、\(\lfloor(n+1)/2\rfloor\) を渡すと負けるとする。
\(\lfloor(n-1)+1)/2\rfloor = \lfloor (n+1)/2\rfloor\)
であるから、 \(n-1\) に対して、相手の応手は \((n-1)-1\) である。\(n=2\) のときに勝ちであるから帰納法により、任意の偶数 \(n\) で勝ちである。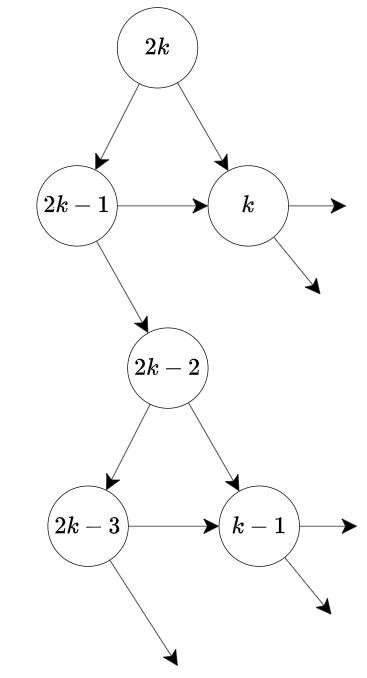 nが奇数の時も含む完全な答えとしては2進法表示したとき \(..0\) または \(..10^{2k+1}1\) ならば勝ち。
nが奇数の時も含む完全な答えとしては2進法表示したとき \(..0\) または \(..10^{2k+1}1\) ならば勝ち。
後退解析。偶奇性よりNが奇数なら\(\mathcal{P}\)。Nが偶数とする。\(N = 4k\) のとき、\([2k+1, 4k]\) には勝ちと負けが交互に現れる。\(i \in [k+1, 2k]\) は \(2i\) に遷移できるので勝ち。\(i \in [1, k]\) は \([k+1, 2k]\) に遷移しても仕方がないので、ここでゲームが閉じている。従って、\(4k, k\) のゲームの勝敗が一致する。\(N = 4k+1\) のとき、\([2k+1, 4k+1]\) には負けと勝ちが交互に現れる。\(i \in [k+1, 2k]\) は \(2i\) に遷移できるので勝ち。\(i \in [1, k]\) は \([k+1, 2k]\) に遷移しても仕方がないので、ここでゲームが閉じている。従って、\(4k+1, k\) のゲームの勝敗が一致する。以上より二進法表示で1が偶数桁にある場合のみ\(\mathcal{N}\)
まずは、色々なBの戦略とそれに対するAの応答を考察するべき。1増やすことでaが3つからa+(1-2a)/5が5つにできる。従って、\(1/2-\varepsilon\)が5つにできる。\(1/2-\varepsilon,1/2-\varepsilon,1/2-\varepsilon\)から\(1-\varepsilon,1/2-\varepsilon,1-\varepsilon\)ができ、\(1-\varepsilon,0,0\)から\(2-\varepsilon,0,0\)ができる。
\(\max (x_i + x_{i+1})\) を \(0\) にする戦略は最適ではない。良以下のような進行が存在する。
\begin{align}
&0.5, 0.5,0.5,0.5,0.5 \\
&0.5, 0.5, 0.5, 0, 0\\
&0.5, 0.75, 0.5, 0.75, 0\\
&0.5, 0, 0, 0.75, 0\\
&1.125, 0, 0, 1.125, 0\\
&1.125, 0, 0, 0, 0\\
&2.125, 0, 0, 0, 0\\
\end{align}
\(0.5, 0.75, 0.5, 0.75, 0\) から \(0.5, 0.75, 0, 0, 0\) としたい。適当にラベルを回転して A の手番で \(x_0 = x_1 = 0, x_4 + x_2 \leq 1, x_3 \leq 1\) が常に成り立つようにしたい。B の手番では \(x_0+x_1+x_2+x_4 \leq 2\) が成り立つので、\(x_0 + x_2 \leq 1\) として一般性を失わない。\(x_4=x_3=0\) とすると \(x_1 \leq 1\) なので ok.
 n=9のとき勝利を阻止できる。H型のタイルを敷き詰める。H中では、斜め・縦・横の長さ3の列が作れないのでOK(Pollak and Shannon). また、8×8サイズのトーラス上でペアを作るHales jewett pairingがある。
n=9のとき勝利を阻止できる。H型のタイルを敷き詰める。H中では、斜め・縦・横の長さ3の列が作れないのでOK(Pollak and Shannon). また、8×8サイズのトーラス上でペアを作るHales jewett pairingがある。2つの山の個数をそれぞれ \(x, y\) と置くと \(|x-y| \geq 2\) が先手が勝つための条件。
真似っこ戦略により、\((x,y)\) と \((x-(a-b),y-(a-b))\) の勝敗が同じ。\(0 \leq x,y < b\) が敗北条件。十分条件であることは明らか。敗北条件を満たさないとする。\(0 \leq x < a – b\) かつ \(b \leq y\) を仮定しても一般性を失わない。このとき \(0 \leq x + b < b \) なので勝利条件を満たすまで再帰的に操作できる。
\(a\) を固定して \(\mathbb{F}_2^n\) の元を \(a, a + x\) でペアリングする。各ペアから一つずつ選んで二つの集合 \(A, B\) を作る。\(S_A = \sum_{i \in A} i, S_B = \sum_{i \in B} i\) と置くと、\(S_A = 0 \lor S_A = a\).
\(\mathbb{F_2}^n\) を2つの集合に分けたとき、要素の和 \(w\) は等しい。よって、\(w\) を持っている方が勝ち。最初に 0 を取ると後手勝ち。先手が選んだ元は \((0, B, x_1, x_2, \ldots)\), 後手が選んだ元は \((A, A+B, x_1 + B, x_2 + B, \ldots)\) とできる。\((A+B, B, x_1, x_2, \ldots), (A, 0, x_1 + B, x_2 + B, \ldots) \) だと和が \(0\) または \(B\) なので元の和は \(A\) または \(A+B\) でどちらも後手が持っている。最初に 0 以外を取ると先手勝ち。
ヒルベルトの基底定理
- Bはある整数 \(1 \leq i \leq 59\) を選ぶ。A は\(a_1, \ldots, a_i\) または \(a_{i+1}, \ldots, a_{60}\) に 1 足し、足されなかった方から 1 引く。
途中で 0 ができるとAの負け。Aが勝つための条件を求めよ(2019 ISL C7)
\(a=(30,29,..,1,2,3,..,31)\) がAが勝利できる最小のMを与える。これが勝利できるのは明らか。勝利する最小のMを考える。\(i < j\) について、\(a_1,\ldots, a_i\) に 1 を足し、\(a_{i+1}, \ldots, a_{60}\) に -1 を足す操作の直後に、\(a_1,\ldots, a_j\) に -1 を足し、\(a_{j+1}, \ldots, a_{60}\) に 1 を足しても勝てるなら M の最小性に反するのでそのような操作は考えない。位置を 1, 2,.., i-1 と指定すると、1 または i に -i が足される。従って、長さ i の区間の端のどちらかは i 以上。最小の要素から区間を伸ばすことで、30,29,..,1,2,..,31 の場合のM未満にはできないことが分かる。
chip-firing game。隣接する頂点に石を配ることを発火(fire)と呼ぶ。
操作が終わらないとする。頂点vが無限回発火すると、その隣接頂点も無限回発火する。従って、サイクルの頂点全てが発火する。各石を区別することにすると、各辺eを通る石を固定しても一般性を失わない。従って、操作が終わらないためには、石がn個以上必要。
逆にゲームが停止するなら、発火しない頂点が存在する。全ての頂点が発火して、停止するとする。最初に発火しなくなった頂点を v とすると、vの隣接頂点がその後に全て発火するため。Björner
石がn個のとき無限回発火する石の配置が存在する。グラフをAcyclicに向き付けて、各頂点に出次数個だけ石を置く。最小の頂点を発火する。最小の頂点に接続する辺の向きを反転する。このときAcyclicな向き付けで各頂点に出次数個の石があるので無限に続く。
隣接する石で完全マッチングを作れるとAの勝ち。完全マッチングが作れるには和が偶数である必要があるので、n=0,3 mod 4 が必要。まず 1 3 4 2 で作れることが簡単に示せる。1, 2, .., 4k で作れるなら 5, 6, .., 4k+4 でも作れる。よって 1, 2, .., 4k+4 でも作れる。1, 3, 2 で作れるので、1, 2, .., 4k+3 で作れる。よって\(n = 0, 3 \pmod 4\) のとき A の勝ち。\(n = 1, 2 \pmod 4\) のとき任意の山の並びに対して、マッチングに選ばれなかった山の位置の偶奇が等しいものが存在するので B の勝ち。
Bは初手で端を取る。端を除いてAの両隣には常にBが配置できるので、Bは引き分け以上にできる。Nが奇数で引き分けならABAB..BAだが、一方の端はBなので起きない。よってB勝ち。Nが偶数で引き分けならABAB..ABとなる。Bが一つでも奇数番目を取れればBの勝ち。N≥8ならば可能。N=2,4,6は引き分け
\(1,2,\ldots,6k\) は mod 3 で 0,1,2 がそれぞれ偶数個ずつあるので完全マッチングを作れて勝敗に影響しない。従って、\(n \leftarrow n \mod 6\) としてよい。n mod 6 = 1,2,3 のとき負け。 4, 5, 0 のとき勝ち
できる。天使がx+y=D/2に到達するまでに x+y=D(0≤x≤D) の点を D/(2k) 個ブロックできる。つまり、D/{2k(D+1)} > 1/(4k) ‰ブロックできる。x+y=D/2からx+y=D/4に到達するまでにさらに到達できる位置のうち 1/(4k) ‰ブロックできる。Dを十分大きく取り、繰り返すと全てブロックできる。
- \(n \geq 2^k\)ならばBが勝つことを示せ
- 任意の十分大きいkに対して、\(n \geq 1.99^k\) であって、Bが勝てるnが存在することを示せ。
(IMO2012)
\(\mathcal{G}(n) = \begin{eqnarray}
\begin{cases}
0 &(n = 0) \\
1 + \lfloor \log_2(n) \rfloor &(\text{otherwise})\\
\end{cases}
\end{eqnarray}\)
\(\mathcal G(n) = \mathrm{mex}_{i + j < n}\ (\mathcal G(i) \oplus \mathcal G(j))\) のとき、\(\mathcal G(i) \oplus \mathcal G(j) \leq \mathcal G(i) + \mathcal G(j)\) なので帰納法より \(\mathcal G(n) \leq n \) が成り立つ(ABC278G)。
\(\mathcal G(n)=\begin{cases}
0 & (n = 0) \\
0 & (n\text{ が偶数}) \\
1 & (n\text{ が奇数})
\end{cases}\)
\(\mathcal G(2^{k+1}x + 2^k) = x\)。\(x / 2 < y < x\) には \(\mathcal G(2^{k+1}y + 2^k) = y\) で遷移可能。\(0 \leq y \leq x / 2\) への遷移は、\(x, y\) の辞書順比較で場合分けをすると、存在が分かる。\(n=2^k\) のとき \(\mathcal{P}\) である。
石を右側から二つずつペアにし、ペアにした石の座標の差を石の個数にするようなニムになる。
取り除けるときの勝敗(Moore’s nim)
各山の個数を2進展開して、各桁について和を取ったとき、すべての和がkの倍数か否か。
\(\mathcal G(a, b)=\nu_2( (a \lor b) + 1)\)
\((a+1)\oplus(b+1)\oplus(c+1)\)がP局面
a, bが最初に相異なる桁e(1-indexed)を用いて \(g(a,b)=|a-b|\oplus|a-b+1|=2^e-1\) と定義する。ただし、\(a=b\) のときは-1とする(補数表現)。山が \(n_1, n_2, \ldots, n_k\) のニム数は \([n_1,n_2,\ldots,n_k]:=\bigoplus n_i \bigoplus_{i < j} g(n_i,n_j)\) になる。
証明(Conway):
\(g(x,y)=g(x\oplus a,y \oplus a)=g(x+ a,y + a)\)が成り立つ。\([n_1\oplus a,n_2\oplus a,\ldots,n_k\oplus a]=[n_1,n_2,\ldots,n_k]\oplus (a\delta_{1,k\bmod 2})\)
\begin{align*}
[0,n_1,n_2,\ldots,n_k]&=\bigoplus n_i \bigoplus g(0,n_i) \bigoplus_{i < j} g(n_i,n_j)\\
&=\bigoplus n_i \bigoplus (n_i \oplus (n_i-1)) \bigoplus_{i < j} g(n_i-1,n_j-1)\\
&=\bigoplus (n_i-1) \bigoplus_{i < j} g(n_i-1,n_j-1)\\
&=[n_1-1,n_2-1,\ldots,n_k-1]
\end{align*}
\(+,\oplus\) でできた式を animating function と呼ぶ。\([x,a_1,\ldots,a_n]\) は animating function で \(\mathbb{N} \setminus \{a_1,a_2,\ldots,a_n\}\) から \(\mathbb{N}\) への全単射であることを示す。\(n=0\) のときは明らか。\(n=1\) のときは \(x \oplus g(x,a_1) = x \oplus g(x\oplus a_1,0) = x \oplus ((x\oplus a_1)-1)\oplus (x \oplus a_1) = a_1 \oplus (x \oplus a_1 – 1)\) より良い。\(n=k-1\) で成立を仮定。\(f_n(x) = x \oplus g(x,a_1)\oplus \cdots \oplus g(x,a_n)\) と置く。\(f_n(x) = f_{n-1}(x) \oplus g(f_{n-1}(x), f_{n-1}(a_n))\) なので \(f_n\) は \(\mathbb{N}\setminus\{a_1,\ldots,a_{n-1},a_n\}\) から \(\mathbb{N}\) への全単射。
\([a_1,\ldots,a_k]=n\) と \(n’ < n\) について、\([a_1,\ldots,a_{i-1},b_i,a_{i+1},\ldots,a_k]=n’\) となる \(b_1,\ldots,b_k\) を取る。\(b_i < a_i\) を満たす \(i\) が奇数個あることを示せば十分。\([0,a_1,\ldots,a_k]=[a_1-1,\ldots,a_k-1]\) なので \(\min a_i \neq 0\) としてよい。任意の \(x\) について \(a_i \oplus x < a_i\) (\(1 \leq i \leq k\)) または \(n \oplus y < n\) のうち成り立つ不等式が偶数個あれば、\(a_1 = 0\) に持ち込めるので、十分。ただし、\(k\) が偶数ならば \(y=0\) 奇数ならば \(y = x\) とする。\begin{eqnarray}
\left\{
\begin{array}{l}
a_i \oplus x < a_i \\
b_i \oplus x < b_i \\
a_i \oplus b_i \oplus x < x
\end{array}
\right.
\end{eqnarray}
のうち成り立つのは偶数個である。例えば、\(a_i\oplus x < a_i\) ならば \(a_i,x\) で相異なる最上位ビットに着目すると、そのビットは \(a_i\oplus b_i, b_i\) の片方でしか立っていないので、\(b_i \oplus x < b_i, a_i \oplus b_i \oplus x < a_i\oplus b_i\) の片方しか成り立たない。以上より、\(a_i \oplus b_i \oplus x < x \) \((1 \leq i \leq k)\) および \(n \oplus n’ \oplus y < x\) のうち成り立つのは偶数個であることを示せばよい。\(a_1, a_2\) が \(g(a_1,a_2)\) が最大となるペアとしても一般性を失わない。このとき、\([a_1,b_2,a_3,\ldots,a_k] = [b_1,a_2,a_3,\ldots,a_k] \iff a_1 \oplus b_2 = b_1 \oplus a_2 \land g(a_1,b_2) = g(b_1,a_2)\) である。よって \(a_1 \oplus b_1 \oplus x < x \iff a_2 \oplus b_2 \oplus x < x\). \([a_3,a_4,\ldots,a_k]=n-[a_1,a_2]\) に対して帰納法の仮定を使えばよい。
ニムの代数構造
足し算は\(a + b = \mathrm{mex}_{a’ < a\\ b’ < b} (a’ + b, a + b’) = a\ \oplus b\) により定義する。
これは、\(a \neq a’\ \Rightarrow a + b \neq a’ + b\) を満たす最も簡単な数を再帰的に定義している。同様に、\(a \neq a’\land b \neq b’ \Rightarrow (a + a’)(b + b’) \neq 0\) となってほしい。分配法則で \(ab = ab’+a’b+a’b’\) とすると、$$ab = \mathrm{mex}_{a < a’\\ b < b’}(ab’+a’b+a’b’)$$ が定義になりそうである。実際、このように定めると、体になる。
次の計算により、$0, 1$ が零元と単位元になっている。
\begin{align}
a0 &= \mathrm{mex}(\emptyset) = 0 \\
a1 &= \mathrm{mex}_{a’ < a}(a0+a’1+a’0)\\
&=\mathrm{mex}_{a’ < a}(a’)\\
&=a\\
\end{align}
交換法則 \(ab = ba\) は定義から明らか。
\(a \neq 0\) かつ \(b \neq 0\) のとき \(a’=b’=0\) とすると \(a’b+b’a+a’b’=0\) なので \(ab \neq 0\) である。言い換えると、\(ab = 0 \Leftrightarrow a = 0 \lor b = 0\) である。\(a’b+ab’+a’b’=ab \Leftrightarrow (a-a’)(b-b’)=0\) だから
\(\mathrm{mex}_{a’ < a \\ b’ < b}(a’b+b’a+a’b’)=\mathrm{mex}_{a’ \neq a \\ b’ \neq b}(a’b+b’a+a’b’)\) である。この事実を交換法則と分配法則の証明に使う。
\begin{align}
a(bc) &
= \mathrm{mex}_{a’ \neq a \\ b’ \neq b \\c’ \neq c} (a’bc+a(b’c+bc’)+a'(b’c+bc’)) \\
&=\mathrm{mex}_{a \neq a \\ b’ \neq b \\c’ \neq c} ((a’b+ab’)c+abc’+(a’b+ab’)c’) \\\\
&= a(bc)
\end{align}が得られる。
足し算は\(a + b = \mathrm{mex}_{a’ < a\\ b’ < b} (a’ + b, a + b’) = a\ \mathrm{xor}\ b\) により定義する。
これは、\(a \neq a’\ \Rightarrow a + b \neq a’ + b\) を満たす最も簡単な数を再帰的に定義している。同様に、\(a \neq a’\land b \neq b’ \Rightarrow (a – a’)(b – b’) \neq 0\) となってほしい。分配法則で \(ab \neq ab’+a’b+a’b’\) とすると、$$ab = \mathrm{mex}_{a’ < a\\ b’ < b}(ab’+a’b+a’b’)$$ が定義になりそうである。実際、このように定めると、体になる。
次の計算により、\(0, 1\) が零元と単位元になっている。
\begin{align}
a0 &= \mathrm{mex}(\emptyset) = 0 \\
a1 &= \mathrm{mex}_{a’ < a}(a0+a’1+a’0)\\
&=\mathrm{mex}_{a’ < a}(a’)\\
&=a\\
\end{align}
交換法則 \(ab = ba\) は定義から明らか。
\(a \neq 0\) かつ \(b \neq 0\) のとき \(a’=b’=0\) とすると \(a’b+b’a+a’b’=0\) なので \(ab \neq 0\) である。言い換えると、\(ab = 0 \Leftrightarrow a = 0 \lor b = 0\) である。分配法則は \(0\) が含まれるときは明らか。それ以外の場合は、帰納法により、
\begin{align}
(a+b)c &= \mathrm{mex}_{a \neq a’\\ b \neq b’ \\ c \neq c’}((a’+b)c+(a+b)c’+(a’+b)c’, (a+b’)c+(a+b’)c’+(a+b’)c’)\\
&= \mathrm{mex}_{a \neq a’\\ b \neq b’ \\ c \neq c’}((a’c+ac’+a’c’)+bc, ac+(b’c+bc’+b’c’)) \\
&= ac+bc
\end{align}となる。\(a’b+ab’+a’b’=ab \Leftrightarrow (a-a’)(b-b’)=0\) だから
\(\mathrm{mex}_{a’ < a \\ b’ < b}(a’b+b’a+a’b’)=\mathrm{mex}_{a’ \neq a \\ b’ \neq b}(a’b+b’a+a’b’)\) である。\(1\) が含まれるときは交換法則は明らか。それ以外の場合は、帰納法により次の様に示す。
\begin{align}
a(bc) &
= \mathrm{mex}_{a’ \neq a \\ b’ \neq b \\c’ \neq c} (a’bc+a(b’c+bc’)+a'(b’c+bc’)) \\
&=\mathrm{mex}_{a \neq a \\ b’ \neq b \\c’ \neq c} ((a’b+ab’)c+abc’+(a’b+ab’)c’) \\\\
&= a(bc)
\end{align}が得られる。
通常の足し算・掛け算は(齟齬がありそうな場所だけ)\(\oplus, \otimes\) で表す。
\(n = 2^{2^k}, \mathcal{P}_n = \{0, 1, \ldots, n – 1\}\) と置く。
- \(\mathcal{P}_n\) は掛け算について閉じている。
- \(\mathcal{P}_n\) は体をなす。
- \(n^2 = n+n/2 = 2^{2^k}+2^{2^{k-1}}\)
- \(\mathrm{msb}(a) = \mathrm{msb}(a^2)\)
- \(\{a^2 : a \in \mathcal{P}_n\} = \mathcal{P}_n\)
- \(\{a^2 + a: a \in \mathcal{P}_n\} = \mathcal{P}_{n/2}\)
- \(a < n\) ならば \(an = a \otimes n\)
\(\mathcal{P}_1 = \{0\}\) が掛け算について閉じているのは明らか。\(r = 2^{2^{k-1}} = \sqrt{n}\) とする。\(\mathcal{P}_r\) が掛け算について閉じていると仮定する。
\begin{align}
(a \otimes r \oplus b)(c \otimes r \oplus d) &= (ar + b)( cn+d ) \\
&= acr^2+(ad+bc)r+bd \\
&= acr^2+(ad+bc)r+bd \\
&=ac(r+r/2)+(ad+bc)r+bd \\
&=acr+ac(r/2)+adr+bcr+bd \\
&=(ac) \otimes r + ac(r/2) + (ad) \otimes r + (bc) \otimes r +bd \\
\end{align}
\(5\) つの項全てが \(r^2 = n\) 未満なので、\(\mathcal{P}_n\) は掛け算について閉じている。掛け算と足し算に閉じているので有限な環をなす。また、零因子が存在しないので逆元が存在して、体になる。
\(\mathrm{msb}(a^2) = \mathrm{msb}(a)\) は
$$ (a \otimes r \oplus b)^2 = a^2 \otimes r + a^2(r/2)+b^2 $$
より帰納法から従う。
\(a^2 = b^2 \Leftrightarrow (a – b)(a + b) = 0 \Leftrightarrow a = b\) なので、\(\{a^2 : a \in \mathcal{P}_n\} = \mathcal{P}_n\) である。\(\mathrm{msb}(a^2) = \mathrm{msb}(a)\) より \(a^2+a \in \mathcal{P}_{n/2}\) である。 \(a^2 + a = b^2 + b \Leftrightarrow (a+b+1)(a-b)=0 \Leftrightarrow a = b, b+1\) であるから、\(\{a+a^2:a\in\mathcal{P}_n\} = \mathcal{P}_{n/2}\) である。
$$an = \mathrm{mex}(a’n+an’+a’n’)=\mathrm{mex}(a’n+(a+a’)n’)$$
\(a’\) を固定して、\(n’\) を動かす。
\(\mathcal{P}_n\) が体であったから、\(\{(a+a’)n’ : n’ \in \mathcal{P}_n\} = \mathcal{P}_n\) である。従って、mex の中身は \(a’ \otimes n \leq i < (a’\oplus 1) \otimes n\) の任意の数を取れる。\(a \otimes n\) は取れないので、\(an = a \otimes n\)。
$$n^2 = \mathrm{mex}_{a < n \\ b < n}(an+nb+ab)$$
\(a=b\) のとき、除かれる数は \(a^2\) となる。\(\{a^2 : a \in \mathcal{P}_n\}=\mathcal{P}_n\) であった。\(b=a + 1\) とすると、除かれる数は \(an+(a+1)n+a(a+1)=n+a(a+1)\) である。\(\{a^2+a : a \in \mathcal{P}_n\} = \mathcal{P}_{n/2}\) であったから、\(n+\mathcal{P}_{n/2}\) が除かれる。以上より、\(\mathcal{P}_n \cup \{n + \mathcal{P}_{n/2}\} = \mathcal{P}_{n+n/2}\) が除かれる。\(n^2+n/2\) が除かれることはないので、\(n^2 = n^2 + n / 2\) である。
\(a \neq b\) かつ \(b \neq a + 1\) のとき、\(a+b > 1\) である。このとき、
$$n(a+b) = n \otimes (a + b) \geq 2n$$
だから \(n + n/2\) が除かれることはない。
排他的論理和が 0 になってはいけない。逆形のときの勝敗を求めよ。(ARC131C)
yuki1613)
駒の有無を2進数の0/1に対応付けると、$$\mathcal{G}(n)=\mathrm{mex}\mathcal{G}(n-2^i)$$ である。3の倍数のペアが作れるので、周期3になる。
奇数番目の山の石の移動は打ち消し可能なので、偶数番目の山の個数の総和がニム数になる。
n が k の倍数のとき \(\mathcal{G}(n) = n / k\) さもなくば \(\mathcal{G}(n) = \mathcal{G}(n – \lfloor n / k \rfloor – 1)\) である。n – n / k = (1-1/k)n なので、O(klog(n)) . \(\lfloor n / k\) が同じ部分をまとめて処理すると O(n / k). よって\(O(\sqrt{n \log(n)})\)
根に複数の子が接続している場合は、各辺ごとに新たに根を作って、それらのニム数のXORを取ればよい。子が一つだけの場合は、その子を根とする部分木のニム数に1足した値が元の木のニム数になる。
赤の辺を1, 青の辺を1とする。例えば、根の辺から順に左から右に書くと
$$111001110$$
のようになったとする。すると、ゲームの値は
$$2+.0011101$$
となる(小数部分は2進表記)。先頭の (1 の個数) – 1 が整数部分、小数部分はそれより後ろの部分の最後に 1 を付け足した値になる。同じ値だが、
\begin{align}
1+1+1-\frac{1}{2}-\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}-\frac{1}{64}
\end{align}という表示もある。帰納法より、一番後ろの辺を削除するのが最善手で、
$$\{2+.00111\ |\ 2+.001111\} = 2+.0011101$$
から従う。
根の子の数が2個以上ある場合はそれぞれに対して新たに根を作った場合の数の和を取ればよい。従って根の子が一つだけの場合のみ考えればよい。根と子を繋ぐ辺が青で、子の部分木のゲームが根付きパスの
$$111001110$$
と同一視できるとする(この値を \(x\) と置く)。すると先頭に 0 を付け足すと
$$0111001110$$となる(この値を \(x’\) と置く)。
\begin{align}
x’ &= -1 + (x – k) / 2^k + (1 / 2 + 1 / 4 + \cdots + 1 / 2^k) \\
&= (x – k – 1) / 2^k
\end{align}である。\(x’ < 0\) となる最小の \(k\) を選べばよい。
左から \(i\) 番目の駒の位置を \(p_i\)、その駒の色を \(c_i\) (青なら 1 赤なら -1)、その駒より右側にある駒(右端2個が同色なら削除を可能回数繰り返した後)の数を \(r_i\) と置く。\(\sum c_i \frac{p_i}{2^{r_i}}\) がゲームの値になる。例えば、一番左側の青駒( i 番目の駒)を左に一つ移動した場合、ゲームの値が $$\frac{1}{2^{r_1}}+\frac{1}{2^{r_2}}+\cdots+\frac{1}{2^{r_{i-1}}}-\frac{1}{2^{r_i}} = -\frac{1}{2^{r_i}}$$だけ変化する。Aさんはこの手が最適である。Bさんも同様に一番左の赤駒を一つ左に移動するのが最適で \(\frac{1}{2^{r_1}}\) だけ変化する。従って、\(x = \{x + \frac{1}{2^{r_1}}| x – \frac{1}{2^{r_1}}\}\) であることを示せばよい。\(x\) の分母が高々 \(2^{r_1}\) なのでよい。
正整数列Aが与えられる。交互にAの要素から1減らす。全ての要素が1回以上減らされたとき、次のプレイヤーの負け。(ARC192B)
Aの要素は偶奇しか関係ない。まねっこ戦略。
Nimの演算
任意の非負整数 \(a, b\) に対して、二ム和 \(a \oplus b\) と二ム積 \(a \otimes b\) を \begin{align} &a\oplus b = \mathrm{mex}
\ \{a’\oplus b: 0 \leq a’ < a\} \cup \{a\oplus b’: 0 \leq b’ < b\} \\
& a \otimes b = \mathrm{mex}\ \{ a’ \otimes b \oplus a \otimes b’ \oplus a’ \otimes b’ : 0 \leq a’ < a, 0 \leq b’ < b\}
\end{align}で定義する。\(a \oplus b = a \ \mathrm{XOR}\ b\).
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 0 | 2 | 3 | 1 | 8 | 10 | 11 | 9 | 12 | 14 | 15 | 13 | 4 | 6 | 7 | 5 | 32 |
| 0 | 3 | 1 | 2 | 12 | 15 | 13 | 14 | 4 | 7 | 5 | 6 | 8 | 11 | 9 | 10 | 48 |
| 0 | 4 | 8 | 12 | 6 | 2 | 14 | 10 | 11 | 15 | 3 | 7 | 13 | 9 | 5 | 1 | 64 |
| 0 | 5 | 10 | 15 | 2 | 7 | 8 | 13 | 3 | 6 | 9 | 12 | 1 | 4 | 11 | 14 | 80 |
| 0 | 6 | 11 | 13 | 14 | 8 | 5 | 3 | 7 | 1 | 12 | 10 | 9 | 15 | 2 | 4 | 96 |
| 0 | 7 | 9 | 14 | 10 | 13 | 3 | 4 | 15 | 8 | 6 | 1 | 5 | 2 | 12 | 11 | 112 |
| 0 | 8 | 12 | 4 | 11 | 3 | 7 | 15 | 13 | 5 | 1 | 9 | 6 | 14 | 10 | 2 | 128 |
| 0 | 9 | 14 | 7 | 15 | 6 | 1 | 8 | 5 | 12 | 11 | 2 | 10 | 3 | 4 | 13 | 144 |
| 0 | 10 | 15 | 5 | 3 | 9 | 12 | 6 | 1 | 11 | 14 | 4 | 2 | 8 | 13 | 7 | 160 |
| 0 | 11 | 13 | 6 | 7 | 12 | 10 | 1 | 9 | 2 | 4 | 15 | 14 | 5 | 3 | 8 | 176 |
| 0 | 12 | 4 | 8 | 13 | 1 | 9 | 5 | 6 | 10 | 2 | 14 | 11 | 7 | 15 | 3 | 192 |
| 0 | 13 | 6 | 11 | 9 | 4 | 15 | 2 | 14 | 3 | 8 | 5 | 7 | 10 | 1 | 12 | 208 |
| 0 | 14 | 7 | 9 | 5 | 11 | 2 | 12 | 10 | 4 | 13 | 3 | 15 | 1 | 8 | 6 | 224 |
| 0 | 15 | 5 | 10 | 1 | 14 | 4 | 11 | 2 | 13 | 7 | 8 | 3 | 12 | 6 | 9 | 240 |
| 0 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 24 |
\(n=2^{2^k}\) \((k \geq 0\)) と置く。このように表せる正整数をフェルマーの2冪と呼ぶ。
- \(0 \otimes a = 0\)
- \(1 \otimes a = a\)
- \(a < n\) ならば \(a \otimes n = an\)
- \((\mathbb{N}, \oplus, \otimes)\) は体
- \(a, b < n\) ならば \(a \otimes b < n\)
- \(a < n\) ならば \(\mathrm{lb}(a \otimes a) = \mathrm{lb}(a)\)
- \(\{0,1,2,\ldots,n-1\} = \{a \otimes a : a < n\}\)
- \(\{0,1,2,\ldots,n/2-1\} = \{a \otimes a \oplus a: a < n\}\)
- \(n \otimes n = \frac{3}{2}n\)
\(a \otimes b = 0 \iff a = 0 \lor b = 0\) を示す。\(a \neq 0 \land b \neq 0\) ならば \(a’=0, b’=0\) とすると、\(a’ \otimes b \oplus a \otimes b’ \oplus a’ \otimes b’ = 0\) なので mex を取ると 0 超になる。\(0 \otimes a=0, 1 \otimes a=a\) は帰納法で容易。iiiを示す。a, b が2冪の場合のみ示せばよい。極大なフェルマーの2冪 \(A,B\) を用いて \(a=cA, b=dB\) と置く。\(a\otimes b =c \otimes d \otimes A \otimes B\). \(A < B\) ならば \(c \otimes d \otimes A < B\) なので \(c \otimes d \otimes A \otimes B =(c \otimes d \otimes A)B < B^2 \leq n\). \(A = B\) ならば \(c \otimes d \otimes A \otimes B = c \otimes d \otimes A \oplus c \otimes d \otimes A / 2 = (c \otimes d) A \oplus ((c \otimes d )\otimes A / 2) \leq A^2 \leq n\) でよい。viを示す。極大なフェルマーの2冪 \(A\) を用いて \(a = cA\) と置く。\(a \otimes a = c \otimes c \otimes A \otimes A = (c \otimes c)A \oplus (c \otimes c \otimes A/2)\). \(\mathrm{lb}(c) = \mathrm{lb}(c \otimes c), (c \otimes c \otimes A/2) < A\) から従う。viiを示す。\(a \otimes a = b \otimes b \iff (a \oplus b) \otimes (a \oplus b)=0 \iff a=b\). \(a \otimes a < n\) と合わせると示せた。viiiを示す。\(a \otimes a \oplus a = b \otimes b \oplus b \iff (a \oplus b)\otimes(a \oplus b\oplus 1) = 0 \iff a = b \lor a = b \oplus 1\). \(\mathrm{lb}(a) = \mathrm{lb}(a \otimes a)\) より \(\mathrm{lb}(a \oplus a \otimes a) = \mathrm{lb}(a)-1\). 以上で示せた。ixを示す。\(n \otimes n = \mathrm{mex}_{a,b < n}\{n \otimes (a \oplus b)= a\otimes= b\}\)= について、viiより \(a=b\) とすると \(0,1,\ldots, n-1\) を取り、viiiより \(n,n+1,\ldots,3n / 2-1\) を取る。\(n= a \oplus b)\) は \(a \oplus b \geq 2\) のとき \(2n\) 以上なので \(3n/2\) は除外数。
\((\mathbb{N}, \oplus, \otimes)\) は体なので、\((a\oplus a’)\otimes(b\oplus b’) \neq 0 \iff a \neq a’ \land b \neq b’\) である。従って、ニム積の定義の \(a’,b’\) の範囲を \(a\neq a’, b\neq b’\) としてもよい。ゲーム \(G, H\) の Conway積は \(G\times H:=\{G’\times H + G\times H’ + G’ \times H’ : G’ \in G, H’ \in H\}\) で定義されて、\(\mathscr{G}(G \times H) = \mathscr{G}(G) \otimes \mathscr{G} (H)\) が得られる。
Nim積の高速な計算
\(A\)をフェルマーの2冪として \(a,b,c,d < A\) とする。
\begin{align}
&(aA + b) \otimes (cA+d) \\
=& (a \otimes c) \otimes (A\otimes A) \oplus (a \otimes d \oplus b \otimes c) \otimes A \oplus (b \otimes d) \\
=& (a \otimes c) \otimes (A/2) \oplus (a \otimes d \oplus b \otimes c \oplus a \otimes c)A \oplus (b \otimes d) \\
=& (a \otimes c) \otimes (A/2) \oplus ((a \oplus b) \otimes (c \oplus d) \oplus b \otimes d)A \oplus (b \otimes d)
\end{align}
により桁数が半分のニム積4つに帰着できるので、桁数の2乗でニム積が計算できる(maspyさん。
Graph Theory (Diestel) の演習問題4 (Chapter2) が面白いと思ったので取り上げてみます。
勝利条件は次の通り。
証明:
\(\Rightarrow\) : 後手は完全マッチングの辺に沿って動かすと必勝。
\(\Leftarrow\) : 対偶を示します。最大マッチング \(M’\) を一つ固定し、\(M’\) に含まれない頂点 \(v\) から先手が始めます。先手は \(M’\) の辺に沿って動かすと必勝です。\(M’\) の辺に沿って動かせないと先手の負けですが、そのとき交互増加道が存在するので、最大マッチングに矛盾。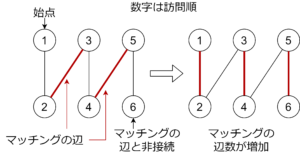
始点が固定されている場合
こんなツイートが届きました。
始点が固定されている場合もオススメです
— 熨斗袋 (@noshi91) September 14, 2021
考えてみましょう……。
勝利条件は次の通り。
証明
\(\Rightarrow\) : 後手は \(M\) の辺に沿って動かすと必勝。動かせなければ、交互増加道が存在して、最大性に矛盾。
\(\Leftarrow\) : 対偶を示します。最大マッチング \(M’\) に沿って先手は動かすと必勝。動かせなければ、交互道が存在して、\(v\) を含まないマッチングが存在しないことに矛盾。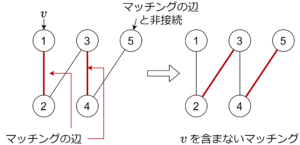
相手が直前に取った石の個数と等しい石の個数を取れないとしたときのNIM(yuki3120)
二部グラフを保ったまま辺を追加するゲーム(ABC398G)
\(x=\min_i a_i, y=\sum_i (a_i-a)\) とする。以下のようなゲームで置き換えられる。\((x,y)\) から \((x,y’)\) (\(0 \leq y’ < y\)) に遷移。または、\((x’,y’)\) s.t. \(x’ < x\) かつ \(x-x’\leq y’ \leq (n-1)(x-x’)+y\) に遷移。
相手が取った石の個数より多く取れないニム(yuki)
Comments