level ancestor problem のアルゴリズムを解説します。

level ancestor problem とは？

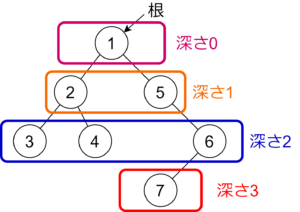例として右のような木を考えよう。頂点 7 の先祖は深さ 0 から順番に 1, 5, 6, 7 である。LA(7,2) は頂点 7 の先祖であって深さ 2 の頂点であるから LA(7,2)=6 である。同様に定義に従って計算すれば、LA(2,0)=1, LA(2,1)=2 となる。

level ancestor problem は木 \(T\) の頂点数を \(N\) として前計算 \(O(N)\)、クエリ \(O(1)\) で処理することができることが知られている。この記事では Michael A. Bender と Martin Farach Colton の The Level Ancestor Problem simplified に基づく手法をお伝えする。この手法では2つの一見、補完関係にないアルゴリズムを組み合わせることで計算量が落とされる。面白いと思う。

ダブリングによる解法

level ancestor problem はダブリングにより前計算 \(O(N\log N)\)、クエリ当たり \(O(\log N)\) で処理することができる。

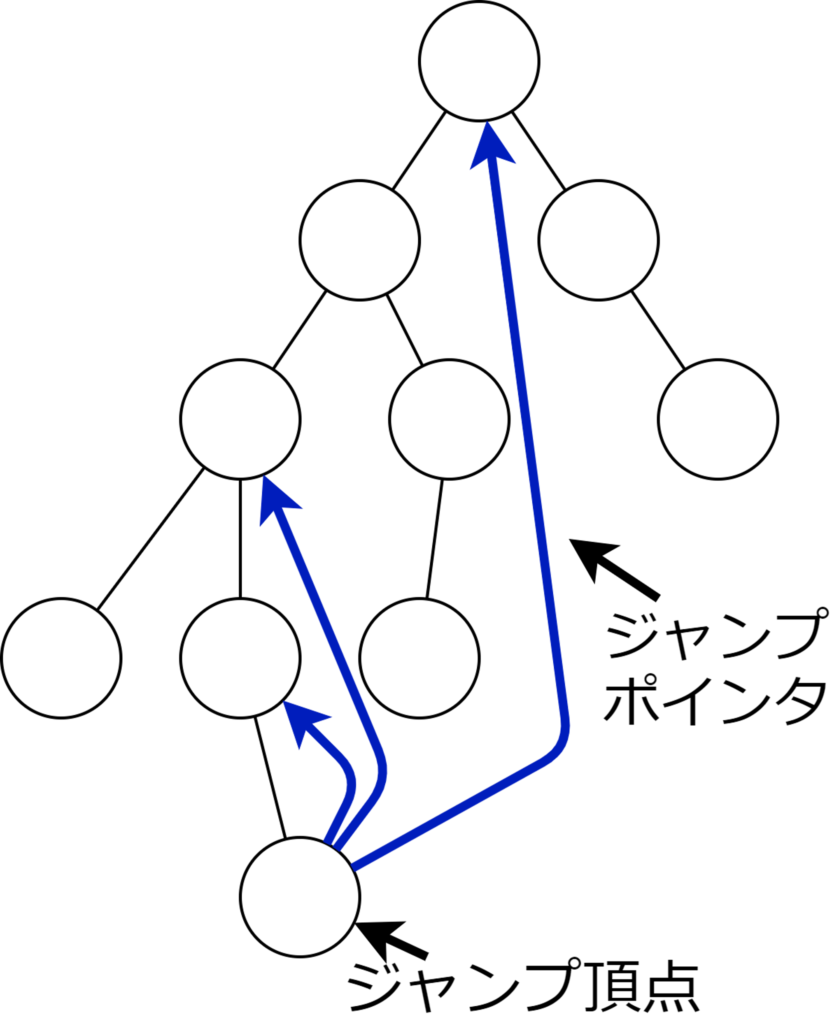
ダブリングでは前計算 \(O(N \log N)\)、クエリ当たり \(O(\log N)\) であった。次に前計算 \(O(N)\)、クエリ当たり \(O(\sqrt{N})\) であるlong-path分解を用いた方法を見よう。

long-path分解による解法

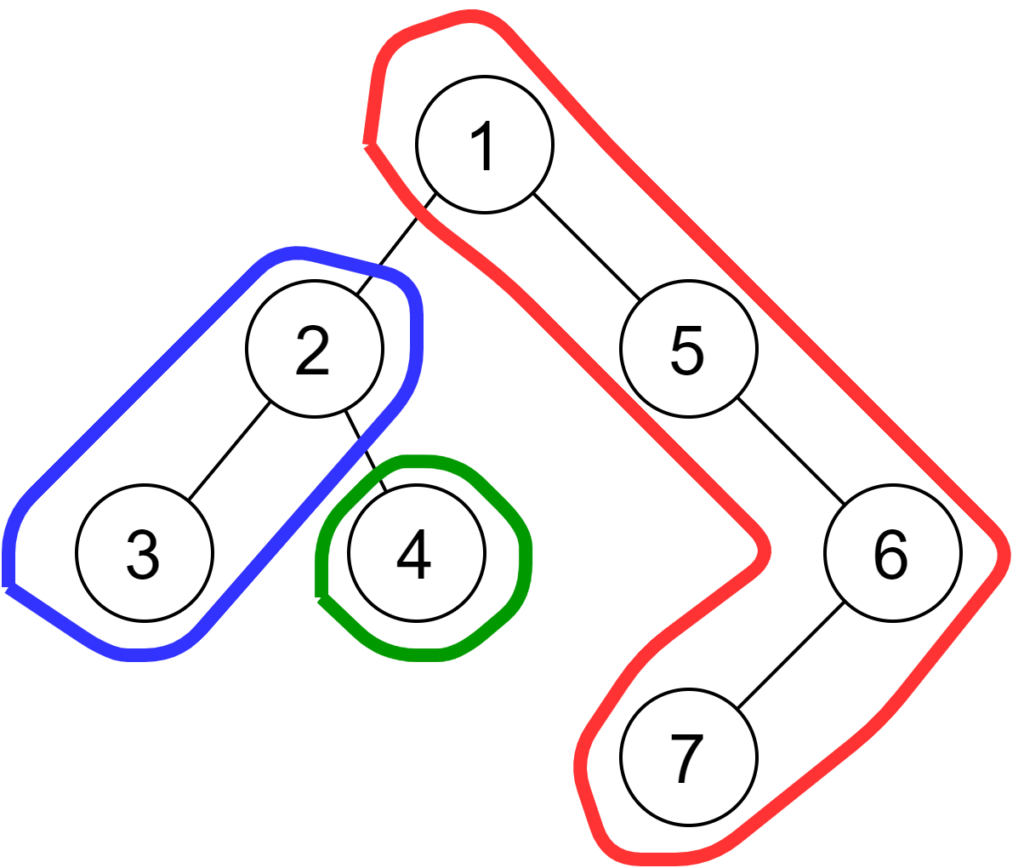
頂点 \(v\) から葉までの最長路の長さを \(v\) の高さという。各long-pathの長さはlong-pathの葉でない端点 \(u\) から葉までの最長路の長さに等しいが、これは \(T\) における \(u\) の高さの定義そのものである。各頂点の高さは \(O(N)\) で列挙できるから、long-path分解は時間計算量 \(O(N)\) で求めることができる。

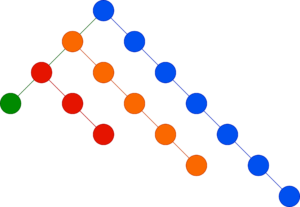右図のようにlong-pathの長さがそれぞれ \(1, 3, 5, 7, \ldots\) という場合を構成できる。long-pathの個数を \(m\) 個とすると、頂点は \(\sum_{i=1}^{m} (2i-1)=m^2\) 個ある。緑の頂点から根に向かえばすべてのlong-pathを経由し、そのlong-pathの個数は \(\Theta(\sqrt{N})\) 個である。

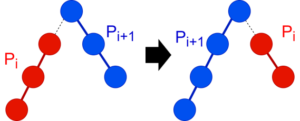あとは経由するlong-pathの個数が \(\Theta(\sqrt{N})\) より大きくならないことを示せばよい。\(i\) 番目 (\(i \leq k\)) に経由するlong-pathを \(P_i\) とする。\(P_j\) は \(P_i\ (j \geq i)\) より先に取り除かれているので \(|P_j |≥|P_i |\) 。\(|P_j |=|P_i |\) ならばより長い道が取れるので矛盾。よって \(|P_j | \geq |P_i |\) である。\(1+2+\ldots+k\leq |P_1 |+\ldots+|P_k | \leq N\) だから \(k=O(\sqrt{N})\)。□

long-pathのはしごへの拡張

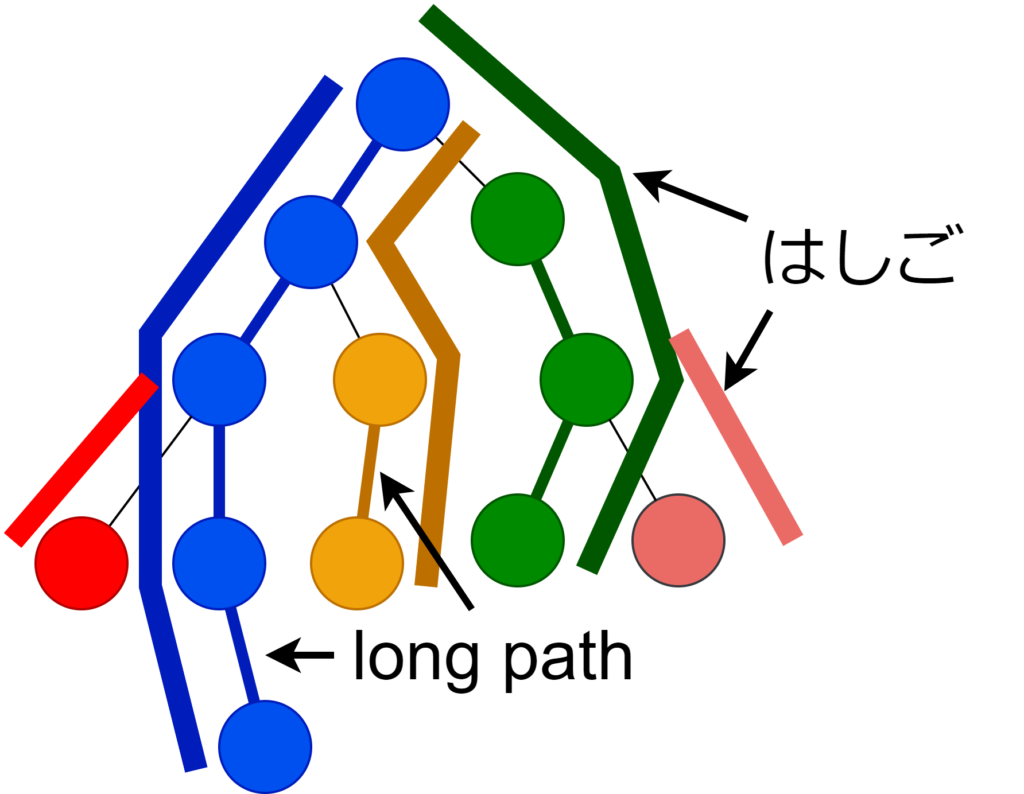
葉から根まで移動するとき long-path を経由する回数は \(O(\sqrt{N})\) であった。前計算 \(O(N)\) を保ったまま path の本数を \(O(\log N)\) に落とす、はしごアルゴリズムを次にお伝えする。

はしごとは long-path を根の方向へ頂点2倍に伸ばした path である。ただし、はしごが根に到達したら、はしごはそれ以上伸ばさない。任意の頂点 \(v\) について、属するはしごの根に最も近い頂点 \(u\) は根であるか、またはその高さ \(h\) について \(h(v) \leq h(u)/2\) が成り立つ。はしごの頂上に移動するたびに高さが2倍になるから、葉から根まで移動するために経由するはしごは \(O(\log N)\) である！ 更にはしごに含まれる頂点数は高々 \(2N\) であるから前計算は long-path 分解と変わらず \(O(N)\) である。

ダブリングとはしごを組み合わせる

以上、ダブリングとはしごアルゴリズムを見た。この2つのアルゴリズムを組み合わせることで前計算 \(O(N)\) 、クエリ当たり \(O(1)\) で計算できることを次に示す。ダブリングは2冪頂点だけ根方向に移動したときの頂点を列挙するから、level ancestor までの経路のうち半分以上を \(O(1)\) で移動できる。移動後の頂点 \(v\) と level ancestor \(u\) の高さ h は \(h(v)\leq 2h(u)\) の関係にあるから、\(u\) から \(v\) ははしごにより \(O(1)\) で移動できる。 ダブリングとはしご法を組み合わせることでクエリ当たり \(O(1)\) で level ancestor が求まった！　しかし、前計算が \(O(N \log N)\) になってしまった。

そこで、次に前計算を \(O(N)\) に改善する。はしごは前計算 \(O(N)\) であったから全頂点について計算してもよい。「2冪頂点だけ根方向に移動したときの頂点」を列挙する始点の頂点をジャンプ頂点と呼ぶことにする。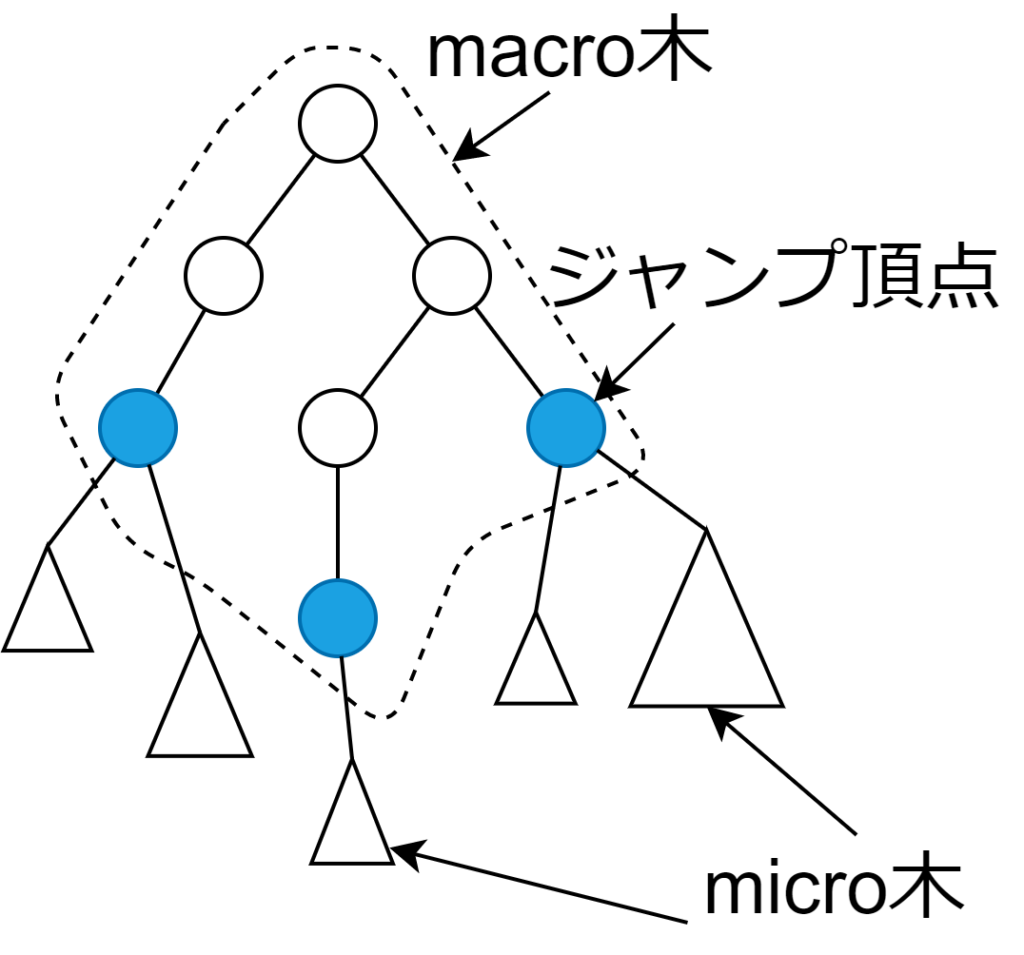ジャンプ頂点一つ当たり \(O(\log N)\) だけ前計算が必要だから、ジャンプ頂点の個数を \(O(N/\log N)\) にしたい。そこで子孫が \(\frac{1}{4}\log_2 N\) 個以上持つ深さ極小の頂点についてのみジャンプ頂点を計算することにする。はしごは高さ2倍の頂点を必ず含むからジャンプ頂点ははしごを利用すれば求まる。木 T をジャンプ頂点を先祖に持つ頂点（ジャンプ頂点自身は含まない）からなるmicro木とそれ以外の頂点からなるmacro木に分解して議論しよう。

\(u\) が \(v\) の先祖かつ \(\mathrm{depth}(u) \geq d\) ならば LA(v, d) = LA(u, d) が成り立つ。例えば、右図では LA(5, 1) = LA(6, 1) = LA(7, 1) = 5 が成り立つ。したがって、macro木の頂点は子孫のジャンプ頂点に移動してから level ancestor を求めれば良い。

micro木の level ancestor は力技で全て求めておく。木を DFS したとき、その上り/下りは０/１に対応付く。例えば右図のDFSは 1101010011011000 にエンコードされる。従って \(n\) 頂点の木の種類数は \(2^{2(n-1)}\) 個以下。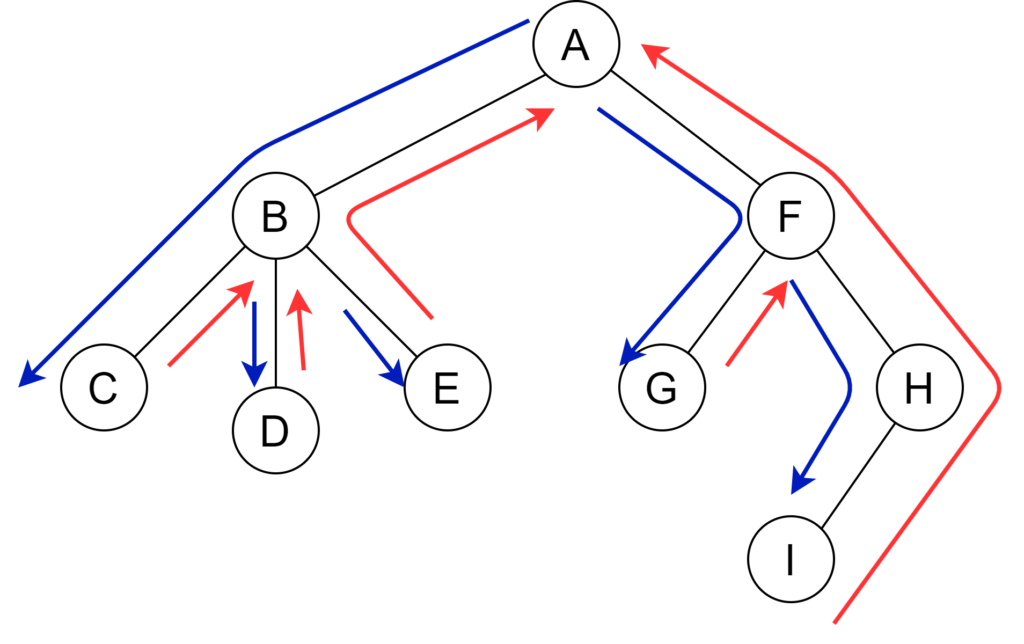micro木のサイズは \(\frac{1}{4} \log_2⁡N\) 以下だからその種類数は \(2^{2(\frac{1}{4}  \log_2N-1)} \leq 2^{\frac{1}{2}  \log_2⁡N }=\sqrt{N}\) で抑えられる。よって各木の形状について全ての level ancestor を愚直に列挙しても 時間 \(O(\sqrt{N}\log^2N)\)で求まる。

以上から micro木とmacro木のいずれでも前計算 \(O(N)\) 、クエリ当たり \(O(1)\) で level ancestor を計算することできた。