永続セグメント木・永続遅延セグメント木のアルゴリズムを解説する。手っ取り早い永続化は、短命配列の代わりに永続配列を使うことである(永続配列の解説はこちら)。しかし、クエリ当りの計算量は、永続配列の計算量 \(O(F(N))\) がオーバーヘッドとして掛かり、\(O(F(N)\log N)\) となってしまう(\(N\)は配列の要素数)。例えば、永続配列として永続二分木を用いると \(F(N)=\log N\) であるから、全体で \(O((\log(N)^2)\) / query である。
この記事ではより効率的な、永続二分木と同様のアイディアでセグメント木を永続化する方法をお伝えする。クエリ当り計算量は \(O(\log N)\) 、\(Q\) 個のクエリ処理後の空間計算量は \(O(N+Q\log(N))\) となる。
永続セグメント木
点更新・区間積取得のセグメント木を永続化する。
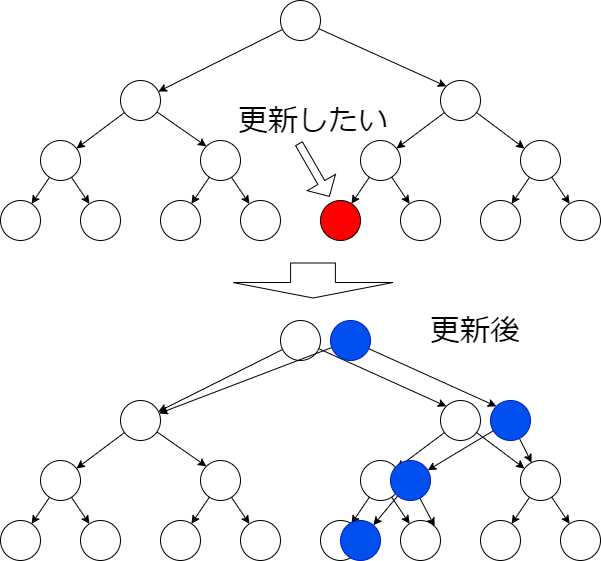
永続化は path-copying によって実現できる。セグメント木の各ノードは右子・左子へのポインタを持つ。点更新の場合、更新部分は根と葉(一つ目の図の赤頂点)を結ぶパス \(P\) になる。永続化するには、パス \(P\) は直接更新せず、 代わりに \(P\) の更新後のパス(二つ目の図の青頂点) \(P’\) を新たに作成する。パス \(P\) と接続する部分木はパス \(P’\) と共有する。更新後のセグメント木にアクセスするには \(P’\) の根から再帰すればよい。セグメント木の高さは \(O(\log N)\) であるから、クエリ当り計算量 \(O(\log N)\)、\(Q\) 個のクエリ処理後の空間計算量 \(O(N+Q\log(N))\) になる。
ちなみに、永続セグメント木は永続配列としても使える。永続二分木を流用した永続配列と計算量は変わらない。つまり、永続セグメント木を持っていれば、永続配列(by 永続二分木)を実装する理由はない。
区間の roll-back
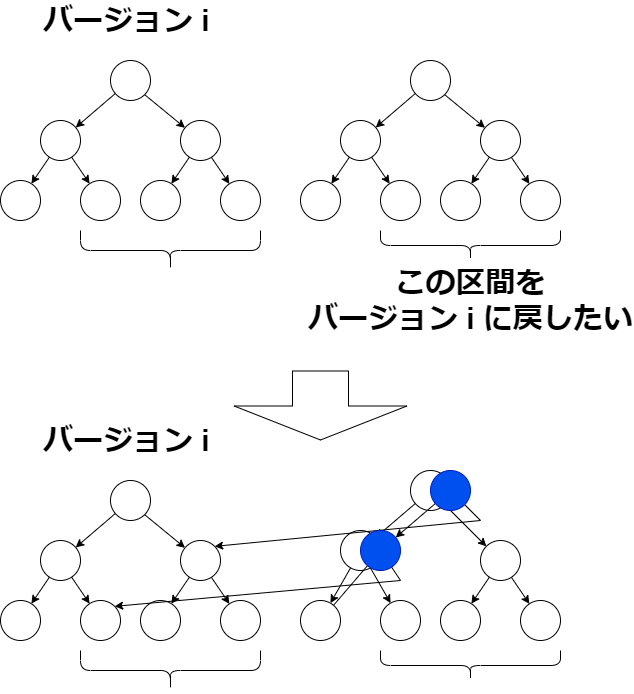
永続(遅延)セグメント木では、区間 \([l, r)\) を時刻 \(i\) の状態に \(O(\log(N))\) で戻せる。これは、下図のように、区間 \([l,r)\) に含まれる頂点に向かうポインタを時刻 \(i\) の頂点に対して張ればよい。あらかじめ、バージョン \(i\) のセグメント木の遅延要素を区間 \([l,r)\) について伝搬させ切る必要があることに注意せよ。
例題
永続が一見必要でない問題を紹介する。問題1はオフライン(クエリ先読み可)でも短命セグメント木では処理できないという点が興味深いと思う。ちなみに、3問とも、Wavelet Matrix を使うと、空間計算量を \(O((N+Q)\log(N))\) から \(O(N\log(N))\) に改善できる。
-
- \(a_{l_i}, a_{l_i+1}, \ldots, a_{r_i-1}\) を昇順に並べ替えたときの \(k_i\) 番目の数字を答えよ。
なお、クエリはオンラインで与えられる。つまり、\(i\) 番目のクエリを処理しないと、\(i+1\) 番目のクエリは与えられない。(出典:SPOJ MKTHNUM)
解法:バージョン \(i\) のセグメント木を \(S_i\) と置く。\(S_{i}\) の区間 \([s, t)\) の頂点に対して、\(a_0,\dots,a_{i-1}\) の項のうち値が \([s,t)\) に含まれるものの個数 \(f(i,s,t)\) を割り当てる。すると、部分列 \(a_l,\ldots,a_{r-1}\) の項のうち値が \([s,t)\) に含まれるものの個数は \(f(r,s,t)-f(l,s,t)\) で表される。
ここで \(f(r,s,t)\) と \(f(l,s,t)\) のどちらも区間 \([s,t)\) の頂点に割り当てられた数である。つまり \(S_l\) と \(S_r\) の二つの根から並行して同一の探索をし、互いの頂点に割り当てられた値の差分を見ることで、\(f(r,s,t)-f(l,s,t)\) を割り当てたセグメント木がシミュレートできる。このセグメント木によって右子・左子の区間に含まれる項の個数 \(p, q\) が分かる。\(p \geq k\) ならば右子に、さもなくば \(k \leftarrow k-p\) として左子に潜ればよい。以上、\(O(N\log(N)+Q\log(N))\) で解けた。
この問題に完全永続は必要なく、部分永続で十分である。クエリを木上のパスに拡張すると、完全永続が必要になる(SPOJ COT, UTPC2011L)。\(r\) 根付き木のパス \(uPv\) 上の列 \(a\) に作用する写像 \(f : \mathbb{Z}^{[N]} \to \mathbb{Q}\) が \(A \leq B \Rightarrow f(A) \leq f(B)\) を満たすとする。このとき\(f_i(x) := f(x|_{[i]})\) は \(i\) の単調増加関数になる。根と頂点 \(v\) を結ぶパス上の列 \(x_v := \prod_{i \in V(rPv)} a_i\) について \(f(x_v|_{\{m2^{k}, (m+1)2^k\}})\) を区間 \([m2^k, (m+1)2^k]\) に乗せたセグメント木を得たい。これは、全永続化によって \(O((N+|V(T)|) \log(N))\) で行える。\(f_i\) は \(i\) の単調増加関数だから、セグメント木上で二分探索ができる。同様に、\(\prod_{i \in V(uPv)} a_i\) についても、$$f\left(\prod_{i\in V(uPv)} a_{i} \right) = f\left(\prod_{i\in V(rPv)} a_{i} \right) f\left(\prod_{i\in V(rPu)} a_{i} \right)f\left(\prod_{i\in V(rP\mathrm{lca}^{\circ}(u,v))} a_{i} \right)^{-2}$$
を用いると二分探索ができる。セグメント木の各ノードが表す区間が右辺の三つで共通していることから、\(\left(\prod_{i\in V(uPv)} a_{i} \right)\)のセグメント木上の二分探索が、シミュレートできる。
例題と同じセグメント木を使えばよい。
hamaduさんの解説。この問題については部分永続で十分である。完全永続化しても、例題のように任意の木上の u-v パスのクエリに答えることはできない(と思う)。根を始点とするパスの部分パスならば答えられる。
永続遅延セグメント木
区間更新・区間積取得の遅延セグメント木を永続化する。
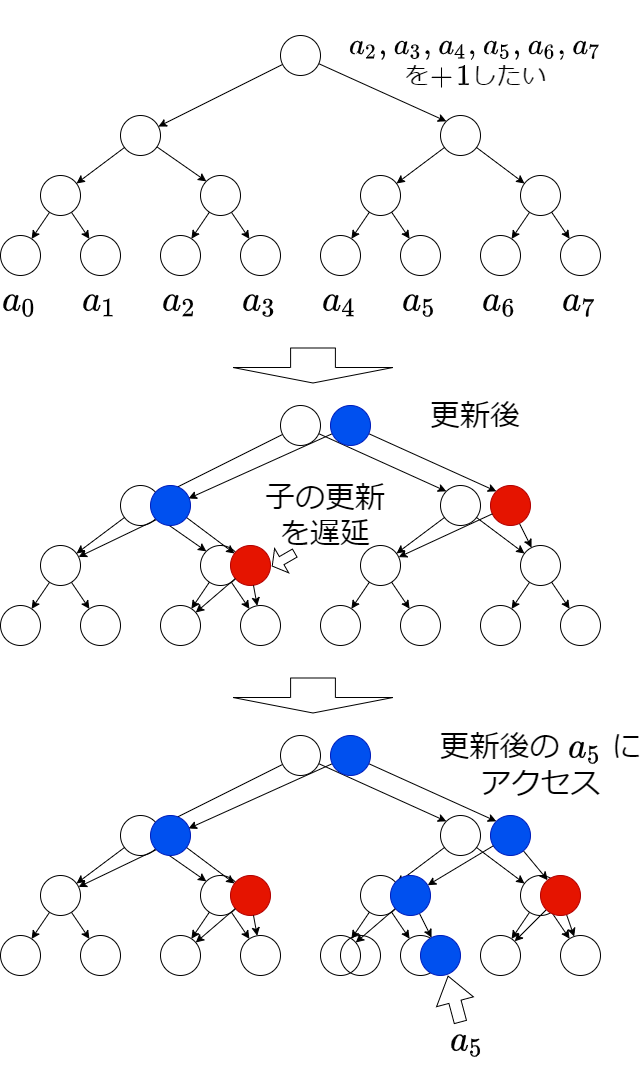
更新後のノードの作成を遅延評価すればよい。通常の遅延セグメント木の更新で訪れる頂点について、元のノードを更新せず、新たに更新後のノード(下図の赤・青ノード)を作成する。また、遅延していた更新(下図の赤ノード)を実行するときも同様に、元のノードを更新せず、新たに更新後のノードを作成する。遅延していた更新を実行するのは、例えば、下の図のように赤ノードの子 \(a_5\) にアクセスする場合や、赤ノードを更新する場合である。
訪れる頂点数は短命遅延セグメント木と同様にクエリ当り \(O(\log N)\) である。従って、永続遅延セグメント木の計算量は、クエリ当り計算量 \(O(\log N)\)、\(Q\) 個のクエリ処理後の空間計算量 \(O(N+Q\log(N))\) になる。
例題
問題:0, 1 からなる文字列 \(T_0=s_0s_1 \ldots s_{n-1}\) が与えられる。文字列を \(Q\) 回操作する。\(i\) 回目の操作では文字列 \(T_i\) の \(t_{l_i},t_{l_i+1},\ldots ,t_{r_i-1}\) のうち、0 を 1 に、 1 を 0 にしたものを \(T_i\) とする。文字列 \(T_0,\ldots,T_{Q}\) のうち辞書順最小のものを出力せよ。(出典:CodeChef SubInversing)
セグメント木 \(S_i\) の区間 \([l,r)\) の頂点に対して、ローリングハッシュ \(\sum_{i=l}^{r-1}t_ib^{i-l} \bmod p\) を割り当てる。すると、 0/1 の反転後の区間 \([l,r)\) は \(\sum_{i=l}^{r-1}b^{i-l} – \sum_{i=l}^{r-1}t_ib^{i-l} \bmod p\) となり、\((b^i)\) の累積和を前計算しておけば \(O(1)\) で求まる。
類題 : CodeForces 464E The Classic Problem
参考文献
- Persistence Made Simple – Tutorial
- ものすごい数の練習問題が載っている。区間の rollback を参考にした。
- つくってなぐろ (永続配列/永続Union-Find木/永続セグメント木の作り方と意義、具体例)
- 二次元平面に特化した場合の永続セグメント木が解説されている。
Comments