フォード・フルカーソンの最大流アルゴリズムは、辺容量が無理数の場合、「有限回で終了しない場合があること」「正しい値に収束しない場合があること」が知られています。そのような具体的な例を紹介します。
残余容量 \(r^n\) の辺に流量 \(r^{n+1}\) を流すと、残余容量 \(r^{n+2}\) となるような \(0 < r < 1\) は $$r^{n+2} = r^{n} – r^{n+1}$$ より \(r = \frac{-1+\sqrt{5}}{2}\) です。下図のような残余ネットワークを考えます。黒色の辺の残余容量は \(\infty\) 、赤色の有向辺の残余容量は \(r^{n+1}, r^n, r^{n+1}以上\) です。青色のパスを増加道として流量 \(r^{n+1}\) を流すと、\(n\) を一つ増やした同様のグラフが得られます。従って、有限回でアルゴリズムが終了しません。また、先の操作を繰り返すと赤色の辺の残余容量は \(0\) に収束しますが、\(s\) – \(t\) 間に他の緑色のような増加道があっても、選ばれることはありません。従って、正しい値に収束するとは限りません。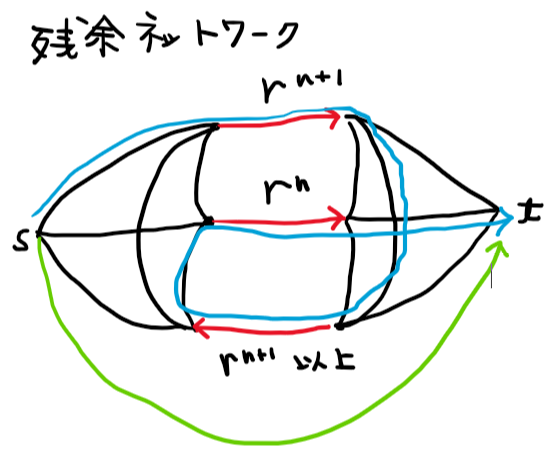
参考文献
組み合わせ最適化(Korte, Vygen)
Comments