目次
inv(w)を順列wの転倒数と置く。
降下集合\(D(w)=\{i:w_i>w_{i+1}\}\)
des(w)=#D(w)
ID=D(w^{-1})
IDはwを数字の昇順に見ていったとき、右から左に戻るときに読んだ要素数の総和の集合と等しい。
\(maj(w)=\sum_{i \in D(w)}i\)
\(\sum_{w \in \mathcal{S}_n} q^{inv(w)} = \sum_{w \in \mathcal{S}_n} q^{maj(w)} =\boldsymbol n!\)
inv, majの母関数がこのようになることは挿入dpで分かる(会長さんの証明)。また、\(inv(w) = maj(\phi(w))\) となる全単射 \(\phi\) が構成できる。
\(w_{n-1} < w_n\) のとき、\(w_{i} < w_{n}\) となる \(i\) が末尾となるように順列を分割して各成分を右に巡回シフト。\(w_{n-1} > w_n\) のとき、\(w_{i} > w_{n}\) となる \(i\) が末尾となるように順列を分割して各成分を右に巡回シフト。このような操作はinvとmajが等しい順列間のbijになる。
\(imaj(w)=maj(w^{-1})\)は\(\phi\)で不変。
\(\sum_{x \in S}q^{f(x)}t^{g(x)}=\sum_{x \in S}q^{g(x)}t^{f(x)}\) となるとき、\(f,g\) は対称結合分布であるという。(inv,maj),(inv,imaj),(maj,imaj)は全て対称結合分布である。
$$\#\{maj(w)=j, imaj(w)=k) = \#\{maj(w)=k, imaj(w)=j)$$
$$\#\{maj(\phi(w))=j, imaj(\phi(w))=k) = \#\{maj(\phi(w))=k, imaj(\phi(w))=j)$$
$$\#\{inv(w)=j, imaj(w)=k) = \#\{inv (w)=k, imaj(w)=j\}$$
$$\#\{inv(w^{-1})=j, imaj(w^{-1})=k) = \#\{inv (w^{-1})=k, imaj(w^{-1})=j\}$$
$$\#\{inv(w)=j, maj(w)=k) = \#\{inv (w)=k, maj(w)=j\}$$
多重集合\(M=\{1^{a_1},2^{a_2},\ldots,m^{a_m}\}\)上の順列全体を \(\mathfrak{S}_M\) と置く。$$\sum_{w \in \mathfrak S_M} q^{inv(w)} = \boldsymbol{n \choose a_1,a_2, \dotsc, a_m}$$
\(\boldsymbol{a_1!a_2!\cdots a_m!}\sum_{w \in \mathfrak S_M} q^{inv(w)} = \boldsymbol{n!}\)
の形を示す。これは、全単射 \(\phi : \mathfrak S_{a_1}\times \mathfrak S_{a_2}\times \cdots \mathfrak S_{a_m}\times \mathfrak S_M \to \mathfrak{S}_n \)であって、左辺の各成分の転倒数の和が右辺の転倒数になるものを構成すれば良い。小さい数から順に割り当てていけば良い。invをmajに変えても同様の式が成り立つ。\(\mathfrak{S}_n\)のときと同様に全単射を作れば示せる。
\(w = w_1 w_2 \cdots w_n \in \mathfrak S_n\) と置く。\(f : [n] \to \mathbb{N}\) が
- \(f(w_1) \geq f(w_2) \geq \cdots \geq f(w_n)\)
- \(w_i > w_{i+1}\) ならば \(f(w_i) > f(w_{i+1})\)
を満たすとき f を w-compatible と呼ぶ。任意の \(f : [n] \to \mathbb{N}^0\) について、w-compatible となる \(w \in \mathfrak{S}_n\) が一意に存在する。\(\mathcal{A}(w)\) を w-compatible となる f 全体、\(\mathcal{A}_m(w) = \mathcal{A}_m(w) \cap [m]^{[n]}\) と置く。
$$\#\mathcal{A}_m(w)= \left(\!\!\!{n+1 \choose m-des(w)-1}\!\!\!\right)$$なので
$$\sum_{m \geq 1} \mathcal{A}_m(w)x^m = \frac{x^{des(w)+1}}{(1-x)^{n+1}}$$
となる。\(|f| = \sum_i f(i)\) と置く。\(\sum_{f \in {\mathbb{N}^0}^{[n]}} q^{|f|} = \sum_{w \in \mathfrak{S}_n}\sum_{f \in \mathcal{A}_w} q^{|f|}\) を計算すると、\(\sum_{w \in \mathfrak{S}_n} q^{maj(w)} = \boldsymbol{ n!}\) が得られる。
隣接swapは逆順列では |p_i – p_{j}| = 1ならば swap(p_i, p_j)になる。
辞書順最小という条件は逆行列において、i=1,2,..を貪欲に手前に置くという条件になる。
maj は逆順列において、値の昇順に見ていったときに右から左に戻る直前の添字の値になる。
木
増加木
順列pが最小値aを用いて、語として \(p_Lap_R\) と書けるとき、p の増加木 \(T(p)\) を、aを根、左子を\(T(p_L)\)、右子を\(T(p_R)\)とした木として定義する。増加木と順列は一対一対応する。
\(a_i\) より小さい要素のうち、最も i の近くにあるものが \(a_i\) の親になる。このようなものはスタックにより線形時間で列挙できるのでデカルト木は線形時間で構築できる。また、O(1)-RMQで線形時間で構築できる。また、オンラインで構築する方法もある。\(a_{n+1}\) を追加したいとする。\(a_n\) に対応する頂点の親を順に辿り、最初に見つけた \(a_n\) より小さいものの子を \(a_{n+1}\) とすればよい。親を辿る回数の合計は順列の長さで抑えられる。\(p_{i-1} > p_i < p_{i+1}\) ならば \(p_i\) は子を二つ持つ。
\(p_{i-1} < p_i < p_{i+1}\) ならば \(p_i\) は右子だけ持つ。
\(p_{i-1} > p_i > p_{i+1}\) ならば \(p_i\) は左子だけ持つ。
\(p_{i-1} < p_i > p_{i+1}\) ならば \(p_i\) は葉である。
ケーリー増加木
子の順序を区別しない多分木に、\([n]\) のラベルを子のラベルが親以上になるように割り当てた木を、ケーリー増加木と呼ぶ。根の子がサイクル分解の標準形の left-to-right minima に対応しているので、\(n + 1\) 頂点のケーリー増加木と \([n]\) 上の順列は全単射の関係にある。この木は \(\phi(i) < i\) を満たす写像 \(\phi : [2, n] \to [n-1]\) と同一視できる。このような写像を後退写像と呼ぶことにする。順列 \(p\) に対して \(a_i = \#\{j : j < i, p_i > p_j\}\) を並べた列 \(I(p) = (a_1, a_2, \ldots, a_n) \) を転倒表と呼ぶ。転倒表は後退写像である。転倒列も後退写像なので、順列と全単射の関係にある。
orderedケーリー増加木
子の順序を区別するケーリー増加木をorderedケーリー増加木と呼ぶことにする。根付き木 \(T\) がorderedケーリー増加木 となるように \([n]\) のラベルを貼る方法は、\(n! / \prod \mathrm{size}(v)\) 通りある。ただし、\(\mathrm{size}(v)\) は \(v\) を根とする部分木のサイズとする。
順列 \(p = p_1p_2 \ldots p_n\) について、\(p_1p_2\cdots p_k\) が \(12\ldots k\) の順列となるような \(k < n\) が存在するとき、\(p\) は分解可能であるという。再帰的に分解を繰り返すことで、任意の順列は、分解不能な順列に一意に分解できる。分解不能な順列の通常型母関数を \(f\) と置くと、$$\sum n!x^n = \frac{1}{1-f}$$ となる。
順列の生成
置換の回数を半分にできる。
perm(a, n) は \(n\) が奇数のとき \(id\)、\(n\) が偶数のとき、\((1\,2\,\ldots\,n-1\,n)\) を \(a\) の左から合成する。\(n\) が奇数の時 \((1\,n)\) を掛ける。このとき、\((1\,n)(1\,2\,\ldots\,n-1) = (1\,2\,\ldots\,n)\) ができる。
\((1\,2\,\ldots\,n)^n = id\) である。\(n\) が偶数のとき \((1\,n), (2\,n), \ldots, (n\,n)\) を順番に掛ける。このとき、\((n\,n) \cdots (2\,n)(1\,n) = (1\,2\,\ldots\,n)\) である。
ランダムな順列の生成
\(\mathfrak{S}_n\)の各元は \(s_1, s_2, \ldots,s_{n!}\) のprefixの積を取ることで全て生成できるとする。\(A = (1, 2), (2, 3), \ldots, (n, n+1)\) とすると、\(\mathfrak{S}_{n+1}\) の各元は
\(A, s_1, A^{-1} , s_2, A , s_3, A^{-1}, \ldots,s_{n!}, A\)で生成できる(Steinhaus–Johnson–Trotter algorithm)。
高々\(\sum |a_i-i|\)回の隣接swapで恒等置換にできるので、\(inv(a)<\leq \sum |a_i-i|\).一回の隣接swapで高々2しか\(\sum |a_i-i|\)が減らないので、\(2inv(a)<\geq \sum |a_i-i|\)
差がk以上の2要素の隣接swapを繰り返すことで生成できるもののうち、逆順列が辞書順最小になるものを求めよ。値が小さい方から貪欲に手前に持っていけば良い。1より前にある値は、元々1より手前にあり、かつ、差がK超であるものと一致する。この集合の中で最も値が小さいものに対して再帰的に処理していくとO(nlog(n))になる(AGC001F)。
二つの順列 \(a, b\) が、\(1 \leq i \leq n – 2\) について \(a_i + b_{i + 2} = a_{i + 1} + b_{i + 1}\) を満たすとする。任意の \(i < j\) について \(a_i + b_j = a_{j-1} + b_{i + 1}\) が成り立つ。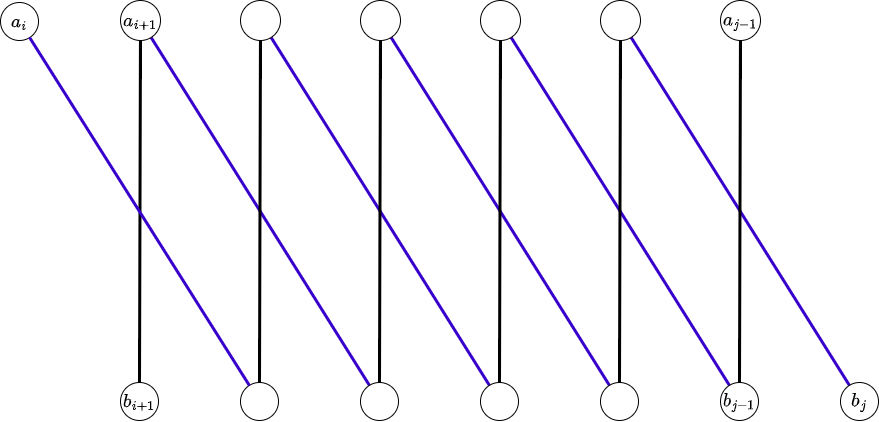 従って、\(b_{n + 1} = b_k\) が成り立つとき、\(i = k-1, j = n + 1\) とすると \(a_{k – 1} + b_{k} = a_{n} + b_{k} \Leftrightarrow a_{k-1} = a_n\) となる。\(a\) の要素は相異なるから、\(k = 1\) である。従って、先頭から順に \(x, a_3+b_3, a_4+b_4, a_5+b_5, \ldots\) となるように \(a, b\) を入れ替えていくとよい。
従って、\(b_{n + 1} = b_k\) が成り立つとき、\(i = k-1, j = n + 1\) とすると \(a_{k – 1} + b_{k} = a_{n} + b_{k} \Leftrightarrow a_{k-1} = a_n\) となる。\(a\) の要素は相異なるから、\(k = 1\) である。従って、先頭から順に \(x, a_3+b_3, a_4+b_4, a_5+b_5, \ldots\) となるように \(a, b\) を入れ替えていくとよい。
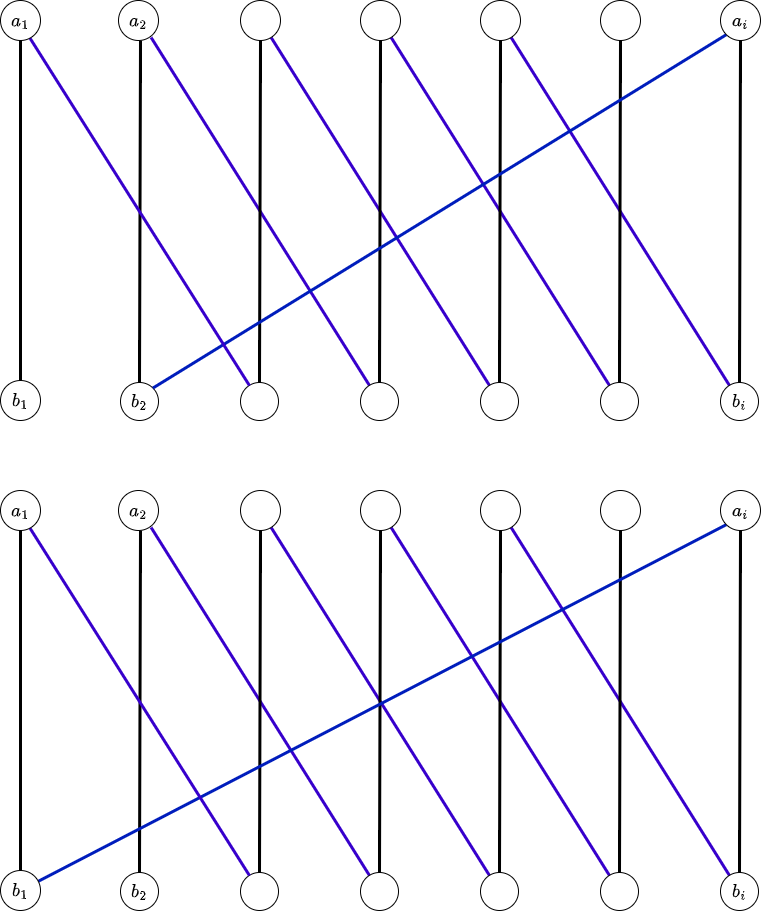
図の2種類しかない。(ref)
相異なる[3n]の要素からなるn個の長さ3の列に対して、先頭の要素のうち、最も小さいものを順番に選んで削除していく。選んだ順序で並べると長さ3nの数列ができる。何通りの数列ができるか、O(n^3)で求めよ(AGC043D)。
後ろから見る。
\((1, 2, \ldots, N)\) の順列 \(P\) の転倒数の偶奇(置換の偶奇)は線形で求められます。
辺 \((i, P_i)\) \((1 \leq i \leq N)\) を貼った有向グラフを \(G\) とします。各頂点の入次数・出自数が共に1なので、\(G\) は交わらない有向閉路の和で表せます。頂点数 \(k\) の閉路
\(a_1 \rightarrow a_2 \rightarrow \cdots \rightarrow a_k \rightarrow a_1\)
に着目します。順列の先頭から \(a_1\) 番目と \(a_2\) 番目を swap すると、自己ループ
\(a_1 \rightarrow a_1\)
と長さ \(k-1\) の閉路
\(a_2 \rightarrow a_3 \rightarrow \cdots \rightarrow a_k \rightarrow a_2\)
に分かれます。従って、長さ \(k-1\) の閉路で再帰的に swap をすると、長さ \(k\) の閉路は、\(k-1\) 回の swap で自己ループ(恒等置換)に分解できます。よって、長さ \(k\) の有向閉路の転倒数の偶奇は \(k-1\bmod 2\) と等しいです。各有向閉路の和を取ると、\(G\) の転倒数の偶奇は (頂点数)−(有向閉路の個数)を \(2\) で割った余りに等しいです。これは、BFS によって線形時間で求められます。実装で楽をしたければ、Union Find でも良いと思います。
長さnの2つの順列a,bが与えられる。任意の \(i \in [n]\) について \(c_i \neq a_i, b_i\) が成り立つ順列 c の個数を求めよ(ABC214G)。a が恒等置換になるようにラベルを張り替えても一般性を失わない。a, b のサイクル分解を考えて、包除原理をする。
連続な添字の集合 \( I = [a, b]\) であって、その像 \(\pi = \{\pi_i : i \in I\}\) もまた連続になるものを区間と呼ぶ。
2つの数列について、順序を保つ全単射があるとき、順序同型と呼ぶ。特に、順序同型な \([n]\) の順列を元の列の簡約形と呼ぶことにする。長さ \(n, m\) の2つの順列 \(\sigma, \tau\) の和を
\(\sigma \oplus \tau = \begin{cases}
\pi(i) & (k\in [1, n])\\
\sigma(i-m)+n & (\text{otherwise})
\end{cases}\) で定義する。また、歪和を
\(\sigma \ominus \tau = \begin{cases}
\pi(i) + m& (k\in [1, n])\\
\sigma(i-m) & (\text{otherwise}) \end{cases}\) で定義する。\((\pi \oplus \sigma)^{-1} = \pi^{-1} \oplus \sigma^{-1}, (\pi \ominus \sigma)^{-1} = \sigma^{-1} \ominus \pi^{-1}\) が成り立つ。
長さ \(m\) の順列 \(\sigma\) と \(k\) 個の非空な順列 \( \theta_1, \theta_2, \ldots, \theta_k\) に対して、膨張 \(\sigma[\theta_1, \ldots, \theta_k]\) を、ブロック \(\theta_1, \theta_2, \ldots, \theta_k\) に分解できる順列であって、それらのブロックを一つの要素とみなしたときに誘導される順列が \(\sigma\) であるものと定義する。\(\sigma\) を分解の商と呼ぶ。任意の順列 \(\pi\) は2つの自明な分解 \(\pi[1, 1, \ldots, 1], 1[\pi]\) を持つ。自明な分解しか存在しない順列を単純であるという。任意の順列 \(\pi\) は一意な単純な商 \(\sigma\) を持つ。仮に、ブロックが3つ以上の相異なる2つの分解が存在したとする。すると、互いに交わるブロック \(A, B\) が存在するが、\(A, B\) の和集合でこれを置き換えられる。従ってブロックが二つの場合に帰着される。また、このことより、商が \(12, 21\) でない限り、\(\pi\) を作る \(\sigma\) の膨張は一意に定まる。例えば単調増加の時は \(1234 = 12[1, 123] = 12[12, 12] = 12[123, 1]\) となって膨張が一意に定まらない。一意にするには、商が \(12\) のときは一つ目のブロックの商が \(12\) でない(\(21\)も同様)という条件を加える必要がある(ref)。順列全体のOGFを \(A\), そのうち商が \(12\) でないものの OGF を \(A^+\), 商が \(21\) でないものの OGF を \(A^{-}\), 単純な順列のうち長さ3以上のものの OGF を \(F\) と置く。\begin{align}
\mathcal{A^+} &= 1 \cup 21[\mathcal{A}^-, \mathcal{A}] \cup \bigcup_{\pi \in \mathcal{F}}\pi[\mathcal{A}, \ldots, \mathcal{A}] \\
\mathcal{A} &= 1 \cup 21[\mathcal{A}^-, \mathcal{A}] \cup 12[\mathcal{A}^+, \mathcal{A}] \cup \bigcup_{\pi \in \mathcal{F}}\pi[\mathcal{A}, \ldots, \mathcal{A}] \\
\end{align}
である。\(B = A^+=A^-\) だから \begin{align}
B&=x+BA+F(A) \\
A&=x+2BA+F(A) \\
\end{align}
となる。\(F\) について解くと \(F = x-A^{-1}(x)-2x^2/(1+x)\) 。商が 12 のときは、商が 12 でない順列の和として一意に表せる。また、商が 21 のときは、商が 21 でない順列の和として一意に表せる。こちらの方法で単純な順列になるまで分解してできる木を代入分解木と呼ぶ。代入分解木は O(n log n) で構築できる。\(\pi(1), \pi(2), \ldots, \pi(k-1)\) によって誘導される代入分解木の部分グラフがすでに構築できているとする。\( \pi(L), \pi(L+1), \ldots, \pi(k)\) が区間であることと、\(k-L+1=\max_{L \leq i \leq k} \pi(i)-\min_{L \leq i \leq k} \pi(i)\) が同値である。これを満たす最大の \(k\) はセグメント木で求まる。
行列の行・列のswapは二部グラフの各部集合の頂点ラベルの張り替えと言い換えられる(ARC107C)。
Gray Code
\((0, 1, \ldots, 2^n-1)\) の順列 p であって、p_i \mathrm{xor} p_{i+1} の bitcount が K となるものを構築せよ。
\(n = k\) でのグレイコード \(p\) が得られているとする。すると、\(p_1, p_2, \ldots, p_{2^k-1}, 2^k+p_{2^k-1}, 2^k+p_{2^k-2}, \ldots, 2^k+p_1\) とすれば \(n = k+1\) でのグレイコードが得られる。\(i\) ビット目は、\(2^i+2^{2i}\mathbb{Z}\) で 1 になるので \(p_i = i \operatorname{xor} \lfloor i / 2 \rfloor\) とすればよい。\(i\mapsto p_i\) は \(\mathbb{F}_2[[x]] / (x^{2^n})\) で \((1+x)\) を掛けることに相当する。\((1+x)^{2^n} = 1\) だからその逆関数は \((1+x)^{-1}(1+x)^{2^n-1} = (1+x)(1+x^2) \cdots(1+x^{2^{n-1}})\) を掛ければよい。これはビット演算で簡単にできる。\(\mathbb{F_2}^{n}\) の基底であって、popcount が K になるものを取れたとする。すると、グレイコードの各ビットにそれぞれの基底を対応させることで、隣接する値の xor の popcount が K になるものが構成できる。K が奇数ならばそのような基底は必ず構成できる。最初の \(K+1\) 個の要素が 1, その他の要素が 0 であるベクトルを \(v\) とする。\(v\) から、ある 1 を 0 にしたベクトル \(K + 1\) 個と、最初の 1 を 0 にしてから、ある 0 を 1 にしたベクトル \(n – K – 1\) 個である(ARC138D)。また、\(p_{2^n}\operatorname{xor}p_1\) の popcount が 1 であるという条件を無視して、\(A, B\) が与えられるので、\(p_1 = A, p_{2^{n-1}} = B\) となるものを構成せよという問題も考えられる。(AGC31C)
\(a_n = a_{n-1}-a_{n-2}\) の場合を意識して計算していく。
\begin{align}
&a_{n} a_{n-2} a_{n-1}^{-1} = 1 \\
&(a_{n} a_{n-2} a_{n-1}^{-1}) (a_{n-1} a_{n-3} a_{n-2}^{-1}) = 1 \\
&a_{n} a_{n-2} a_{n-3} a_{n-2}^{-1} = 1 \\
&a_{n} a_{n-2} (a_{n-5}a_{n-6}^{-1}a_{n-5}^{-1}) a_{n-2}^{-1} = 1 \\
\end{align}
\(a_na_{n-3} a_{n-4}^{-1} a_{n-1}^{-1}=a_na_{n-2}a_{n-1}^{-1}=1\) より \(a_n a_{n-3} = a_4a_1 = A\) であるから、\(a_nAa_{n-6}A^{-1}=1\). (ref)
超置換
全ての \([n]\) の順列が部分文字列として現れる列を超置換と呼ぶ。\(a = (n,n-1,\ldots, 1), b = (n-1,n)(n-1, n-2, \cdots, 1)^2\) と置く。接尾辞を順列 \(p = p_1p_2 \cdots p_n\) から順列 \(ap\) に変化させるには末尾に \(a_1\) を加えればよい。順列 \(bp\) に変化させるには末尾に \(a_2a_1\) を加えればよい。逆に1文字加えて別の順列に変化させるのは \(a\) 、2文字加えて別の順列に変化させるのは \(b\) だけである。頂点集合を \(\mathcal{S}_n\) とする有向グラフを考える。任意の相異なる頂点 \(u, v\) に対して、有向辺 \((u, v)\) が張られており、その重みは接尾辞を \(u\) から \(v\) にするために末尾に加える必要がある最小の文字数とする。辺集合 \(E_B=\{(\pi, b\pi) : \pi \in \mathcal{S}_n\}\) の各辺について \(\pi\) を \((a^{n-1}b)^i\pi\) で置き換えると移りあうもの同士を同じ色で塗る。頂点は \(a\) を何回か掛けて移り合うものを同じ色で塗る。\(ba^{n-1} = (n-1, n)(n, n-1, \ldots, 1) = (n-1, n-2, \ldots, 1)\) である。\(\operatorname{ord}(a) = n, \operatorname{ord}(ba^{n-1})=n-1\) である。超置換に表れる、重み 2 の辺の色の種類数と重み 3 以上の辺の個数の和は \((n-2)!-1\) 以上である。
- ある色の頂点を全て訪れた直後の異なる色の頂点への遷移
- 初めてのある色の辺の遷移
この二つの遷移は重みが2以上である。また、この二つを同時に満たす遷移 \((u, v)\) が存在するならば、\(a^{-(n-1)}u\) への遷移は重み 3 以上である。従って、超置換の長さの下限は \(n-3+n!+(n-1)!+(n-2)!\) であることが分かる(ref)。
\(i < P_i, i = P_i, i > P_i\) を満たす i の個数がそれぞれ A, B, N-A-B 個の順列の個数は包除原理により\(O(N^2)\)で求まる(cpsco2019)。
任意の \(i \in [n]\) について \(|p_i-i| \neq K\) を満たす順列の個数を \(O(n \log n)\) で求めよ(AGC005D)
置換を左から掛けるのは終域(ラベル)の置換、右からかけるのは始域(添字)の置換になっている。
(a b .. z ω) (ω A B .. Z) = (a b .. z A B .. Z ω)
(1 2 .. n)
= (2 1) (1 3 .. n)
= (2 1) (3 1) .. (n 1)
(1 2 .. n)
= (1 2 .. n – 1) (n 1)
21x→x12
2xy→yx2
順列 p に対して、順列 (n+1-p_i) を補順列 p^c と呼ぶことにする。
2つの順列P,Qがある。2つの数列の先頭から好きな順で選んだときにできる数列の個数を求めよ(New Year Contest 2015 : I – マージ)
n-1個の互換 \((u_1, v_1), \ldots, (u_{n-1}, v_{n-1})\) の積が \(1, 2, \ldots, n\) の巡回置換になることと、\(G = ([n], \{(u_i, v_i)\})\)が木てあることが同値である。これは帰納法から分かる。
パターンの包含に関して順序を作ると、\((n-1,1,2,\ldots, n-2, n)\)の形の順列は無限反鎖をなす(n-1の箇所が固定される)。
(0,1), (1,0) のステップからなる経路であって各辺に順に数\(a_1, a_2, \ldots, a_n\)が割り振られたものを考える。同じ向きのstepが連続しているとき、ラベルは公義単調減少、直角に交わっているときは\(e_{i}+e_{i+1}\leq i+1\)を満たすとする。\(e_1=1\)と置く。このような経路全体は長さnの順列と一対一対応がある。挿入dpで順列を作っていくときの、挿入する位置を\(a_i\)とすれば良い。
Schreier-Simsのアルゴリズム
\(G=\langle S \rangle \)に対して \(|G|\) を求めたい。軌道・固定群定理により \(|G|=|Gx||G_x|\)。\(|Gx|\)はBFS/DFSで求まる。\(H=G_x\) の生成集合 T が分かれば、G←H, S←Tとして再帰的に処理できる。
\(s_1,s_2,\ldots,s_k \in S\) について、\(s_1s_2\ldots s_k \in G_x\)とする。\(G/G_x\) の代表元の集合を \(A\) と置く。このとき、前から処理することで、\(\prod s_i = \prod (a_is_ia_i’)\) (\(a_i,a_i’ \in A, a_is_ia_i \in G_x\)) の形にできる。従って、\(G_x\) の生成元は \(asa’ \in G_x\) (\(a,a’ \in A, s \in S \)) 形の元を列挙すればよい。
置換群S_nの部分群の生成集合の大きさはn(n-1)で抑えられる。これは、iの降順に固定群にしていけばよい。i,jのすわっぷがにど現れればキャンセルできる。
また、n-1で抑えることもできる。各生成元gについて、スワップする要素のうち最小の要素がi(g)だとして、辺(i, gi)を張ったグラフを考える。生成元を追加して閉路ができたとする。この閉路の最小の要素から順に閉路の総積xを取ると、i(x) < i(g)。生成集合からgを削除して、xを加える。この操作を閉路がなくなるまで繰り返せばよい。
N 人の人が N 個のマスに順番に座りに来る。空いているマスからランダムに選んで座る。ただし、隣に誰か座っていると、座らずに立ち去る。N → ∞ としたときに i 番目の人が椅子に座れる確率を求めよ(WTF19-F)。
時刻 T に起きる確率の母関数を f, 時刻 0 に起きた後、時刻 T に再度起きるする確率の母関数を g とすると、時刻 T に初めて起きる確率の母関数 h との間に hg = f が成り立つ。\(h = \frac{f}{g}\) より、初めて起きる時刻の期待値は \(\frac{d}{dx}h |_{x=1}=\frac{f'(1)g(1)-f(1)g'(1)}{g(1)^2}\) となる。
N 個の非負整数の組 \(A=(A_1,A_2,\ldots,A_N)\) が与えられます。高橋君は N 個のカウンターを持っており、最初、全てのカウンターの値は 0 です。高橋君は、全ての 1≤i≤N について i 番目のカウンターの値が \(A_i\) 以上となるまで次の操作を繰り返します。N 個のカウンターの中から 1 つを等確率に選び、その値を
0 にする。選んだカウンター 以外のカウンターの値を 1 増加させる。高橋君の操作回数の期待値を O(N log N) で求めよ(ABC270H)。
順列\piに対して、転倒している添字同士を結んだ無向グラフをG[\pi]と書き、転倒グラフと呼ぶ。
G[\pi]の補グラフは\piを逆順に並べた置換の転倒グラフである。転倒グラフは比較可能グラフである。逆にGと\bar Gの両方が比較可能グラフであることと、Gが転倒グラフであることが同値。Gと\bar Gが比較可能グラフとする。向き付けた辺集合F,F’について、(V,F+F’)はDAG。(V,F^R+F’)もDAG。それぞれpos,valに対応していて、転倒グラフが作れる。
無向グラフについて、その頂点ラベルをposとする転倒グラフが存在することと、v+#{u ∈ N(v):u > v} v- #{u ∈ N(v):u < v}が全単射であることが同値。帰納法で示せる。
/p>
\([n]\) の多重順列について、\(S\)の要素が現れるならば、それより後ろに\(T\)のも現れるという条件が複数与えられる。\(O(n2^n)\) でそのような列の個数を求めよ(ARC158F)。
過半数
相異なる要素2つの要素を取り除いても、過半数を占める値は変化しない。このことから、O(N)で過半数を占める値が求まる(Boyer–Moore majority vote algorithm)。
各値 \(v\) について、それを過半数の要素とするような部分列を考える。そのような部分列に含まれうる位置の個数を \(c_v\) とすると \(\sum c_v \leq 4N\) となる。これは、Ballot数列と同様の証明で、1+(-1) / (-1)+1 をペアにして消去すると示せる。この事実を用いると、過半数を占めるような値が存在するような部分列への分解の個数が O(N) で数えられる(ARC159F)。隣り合う相異なる2要素を削除することを繰り返して空文字列にできることと、Nが偶数かつ過半数を占める要素が存在することが同値(ARC159F)
次の二つについて、全単射がある。辺 \((i, a_i-1)\) を張ればよい。
- \(0 \leq a_i \leq i\) を満たす長さ \(n\) の整数列 \(a\)。ただし、各正整数は高々一度しか現れない。
- \(0, 1, \ldots, n\) を頂点とし、いくつかの点素な有向パスからなるグラフ。ただし、各パス \(v_0,v_1,\ldots, v_k\) について \(v_0 > v_1 > \cdots > v_k\) が成り立つ。
長さ \(n\) の条件を満たす整数列 \(a\) 全てに対する、長さ \(K\) の狭義単調減少部分列の個数の和が \(O(n \log(n))\) で求まる(ARC138)。
p_i と p_j の swap
i, j が同じサイクルに含まれていたなら、別々の2つのサイクルに分裂
i, j が異なるサイクルに含まれていたなら、一つのサイクルに合体
$y:=gxg^{-1}$ となる置換 $g$ が存在する置換 $y$ を $x$ の共役という。
置換は巡回置換の直積とみなせるが、共役な元では巡回置換の長さが重複を込めて、同じになる(!)。
証明:$y^k g =gx^k$ であるから、$x$ における $(x_1, x_2, \ldots, x_n)$ という巡回置換は $(gx_1, gx_2, \ldots, gx_n)$ という巡回置換になる。
gwcontest2015 E問題(snukeさん)
$a = (1, 2, \ldots, N)$ に対して、
巡回置換 $S_i=(i, i+1, \ldots, i+L-1)$
を何度でも適用できる。
どのような置換が表せるか?
(共役を使った解法)$T_i := S_i^{-1}S_{i+1} = (i, i+L-1, i+L)$ は長さ 3 の巡回置換になる。
共役で作用する位置を置換すると、$T’_i:=S_{i+1}^2T_iS_{i+1}^{-2} = (i, i+1, i+2)$ となる。$T’_i$ 全体は偶置換全体を生成する。一方、$S_i$ は偶置換/奇置換(Lが奇数/偶数)なので、偶置換全体/置換全体が生成される。
ソート
順列 p に対して、\(|i-j| = p_i\) または \(|i-j| = p_j\) のとき \(p_i\) と \(p_j\) を swap できる。ソートする手順を示せ(TTPC2015I)
\(p_i\) と \(p_{(i+p_i) \bmod n}\) を swap できる。ソートする手順を示せ(ARC110F)
interchangeによるソート
反転を \(\cdot^R\) で表すことにする。\((a^Rb)^R = b^R a\) は \(b\) の長さが \(1\) ならば巡回置換になる。
- 奇数長のprefixの反転のみでソートできるか。ソートできるなら5n/2回以下でソートせよ。(CF1558C)
数列Aが与えられる。順列Pのうち、Q[i]=min(P_[(i-1)%N],P[i])で置き換える操作を何回か行って数列Aにできるようなものの個数を求めよ。(天下一2018F)
(1 x) の形の互換を高々 3n/2-1回掛けることで恒等置換にできる。これは、最初に1を含まない長さ2以上のサイクルを、1を含むサイクルにまとめるのにn/2-1回、それらを恒等置換にするのにn回かかるからである。
\(p_1, .., p_n\) と \(p_{n+1}, .., p_{n+m}\) の2要素を交換できるとき、何回操作すると恒等置換にできるか求めよ。
\((1,2),(2,3),(3,1)\) をそれぞれ \(A,B,C\) 回行って、恒等置換になるものは何通りあるか(yuki1655)。\(a^2=b^2=(ab)^3=1\) の下、各操作は \(a, b, aba\) で表せる。二個ずつ操作を区切ってみる \(aa=bb=1, ab, ba\) の何れかになり、数えられる。
置換二つ \(x, y\) の生成する群の位数 \(2\operatorname{ord}(xy)\) で二面体群である(yuki2045)。
数列 \(a_1, \ldots, a_n\) を分割した2つの数列 \(B=(a_1, a_2, \ldots, a_d), C=(a_{d+1},\ldots,a_n)\) をマージして数列Dを作る。ただし、B, CはDにおいて部分列をなす。この操作は基数2の基数ソートの逆操作になっている。極大増加連続部分列の個数 \(k\) に着目すると \(\lceil \log_2(k)\rceil\) 回でソートできる。これが最小である。i回目の操作のコストが \(dC_i\) で与えられるとき、L回以内にソートするための最小コストが計算できる(AGC062B)。
サイクルの個数
$$\exp(y\log(1/(1+x)) = \left(1+x\right)^{-y} = \sum_{i \geq 0} y(y+1)\cdots(y+i-1)x^i/i!$$
2つ目の式は \(y\) 色で塗る方法を数えていると捉えると、各色毎にサイクル分解の標準形を割り当てている。3つ目の式は、サイクル分解の標準形に昇順に要素を追加している。\(k\) は、先頭に追加した場合だけ左から右への最小値になるので、\(y + k-1\) を掛けている。各サイクルの要素の最小値の積を重みとしたときの、サイクルの個数毎の母関数を求める問題が出題されている(Cyclic GCDs)。
Comments