\(m\) 個の同種の機械と \(n\) 個のタスクがある。一つの機械が各タスクを処理するのに必要な時間は正整数 \(t_1,\ldots,t_m\) で表される。同じタスクを複数の機械で共有して処理することはできない。タスクを全て処理するのに必要な最短時間を求めよ。
次の超簡単なアルゴリズムで2近似になる。
2近似アルゴリズム:タスクの処理が完了した機械には、すぐに別のタスクを割り振る
近似率の証明:一般性を失わず、最後に完了したタスクの時刻が、機械 \(1,2,..,m\) に対して広義降順としてよい。機械 \(i\) に割り当てられた \(n_i\) 個のタスク \(a_{i,1},..,a_{i,n_i}\) が割り当てられたとする。タスクが割り振られる時刻では、全ての機械は動作中ないしはちょうどタスクを終了したところであるので、任意の \(i\) に対して $$\sum_{j < n_1} t_{a_{1,j}} \leq \sum_{j \leq n_i}t_{a_{i,j}} $$が成り立つ。従って、\(\mathrm{OPT} \geq \sum_{j < n_1} t_{a_{1,j}}\) である。\(\mathrm{OPT} \geq t_{a_{1, n_1}}\) でもあるから、\(2\mathrm{OPT} \geq \sum_{j \leq n_1} t_{a_{1,j}}\) が成り立つ。つまり、2近似になっている。
処理時間 \(1\) のタスクが \(x(m-1)\) 個、処理時間 \(x\) のタスクが1個あるとすると、上記のアルゴリズムでは完了時刻が \(\lfloor \frac{x(m-1)}{m}\rfloor + x \ \to 2x \ (m\to\infty)\)、最適な場合 \(\mathrm{OPT}=x\) だから、確かに2近似になっている。\(x=4, m=5\)とすると下図のようになる。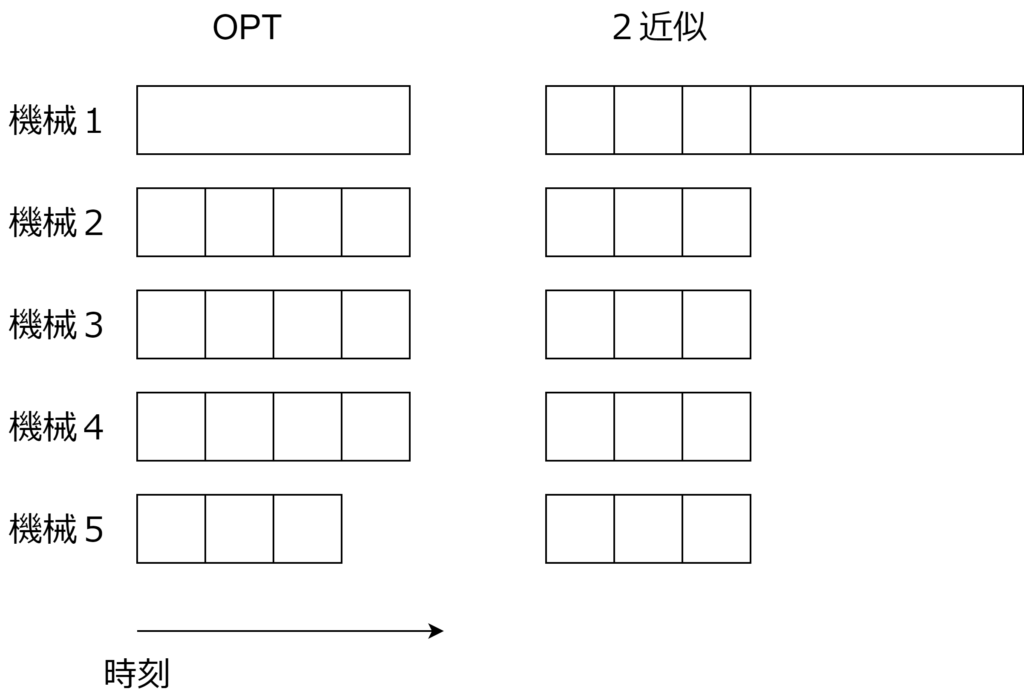
2近似のアルゴリズムのタイトな例は、処理時間の長いタスクが最後に処理されて発生していた。そこで、処理時間の大きい順に処理すると、1.5近似のアルゴリズムが得られる。
1.5近似アルゴリズム
- タスクの処理が完了した機械には、すぐに別のタスクを割り振る
- 処理時間の長いタスクから順に割り振る
1.5近似の証明:\(T=\sum_{j < n_1} t_{a_{1,j}},t=t_{n_1}\) と置くと、\(mT+t \leq m\mathrm{OPT}\) が成り立つ。終了時刻 \(\tau=T+t\) について解くと、$$\tau\leq\mathrm{OPT}+\left(1-\frac{1}{m}\right)t$$ となる。
(i) \(t \leq \frac{\mathrm{OPT}}{2}\) の場合、\(\tau \leq \mathrm{OPT}+\left(1-\frac{1}{m}\right)\frac{\mathrm{OPT}}{2} \leq \frac{3}{2}\mathrm{OPT}\) となる。
(ii) \(t > \frac{\mathrm{OPT}}{2}\) の場合、任意のタスクの処理時間が \(\frac{\mathrm{OPT}}{2}\) より大きいので \(m \geq n\) である。さもなくば、どのように割り振っても、ある機械に二つ以上タスクが課され、完了時間が\(\mathrm{OPT}\) 超になるので矛盾。よって、1.5近似のアルゴリズムでは、各機械に高々一つしかタスクが課されないので、完了時間 \(\mathrm{OPT}\) の割り振りになる。
(i) \(t \leq \frac{\mathrm{OPT}}{2}\) の場合、\(\tau \leq \mathrm{OPT}+\left(1-\frac{1}{m}\right)\frac{\mathrm{OPT}}{2} \leq \frac{3}{2}\mathrm{OPT}\) となる。
(ii) \(t > \frac{\mathrm{OPT}}{2}\) の場合、任意のタスクの処理時間が \(\frac{\mathrm{OPT}}{2}\) より大きいので \(m \geq n\) である。さもなくば、どのように割り振っても、ある機械に二つ以上タスクが課され、完了時間が\(\mathrm{OPT}\) 超になるので矛盾。よって、1.5近似のアルゴリズムでは、各機械に高々一つしかタスクが課されないので、完了時間 \(\mathrm{OPT}\) の割り振りになる。
Comments