巡回セールスマン問題（Traveling Salesman Problem, TSP）とは、重み最小のハミルトン閉路を求める問題である。一般には、TSPは近似アルゴリズムですら、NP困難であることが知られている。しかし、重み関数が三角不等式を満たし（メトリックであり）、負の重みを含まない場合に限れば、クリストフィードのアルゴリズムによって1.5近似を \(O(n^3)\) で求めることができる（\(n\)は頂点数）。
三角不等式が成り立つ（メトリックである）とは、任意の３頂点 \(x, y, z\) について \(c(x, z) \leq c(x, y) + c(y, z)\) を満たすことである。例えば、ユークリッド距離はメトリックである。
2近似
2近似のアルゴリズムは次の通り。
- \(G\) の最小全域木 \(T\) を構築する。
- \(T\) の各辺をコピーして二重辺にしたあと、オイラー閉路 \(C’\) を構築する。
- \(C’\) の頂点を順番に走査し、二度目以降に出現した同一頂点を削除して、ハミルトン閉路 \(C\) を得る。例えば、-x-y-z- というパスが \(C’\) に含まれていて、y がすでに出現していたなら y を削除して -x-z- とする。\(C\) が2近似のハミルトン閉路になっている。
メトリックより中継点を削除して距離が増加しないから、\(c(C) \leq 2c(T) \) である。
以上より、
$$\frac{c(C)}{c(C^\star)} \leq 2 $$となる。
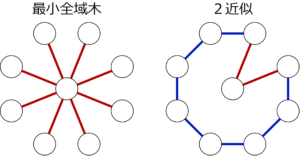
タイトな近似例は下図。\(K^n\) の真ん中の頂点から最小全域木を走査すると２近似の例が得られる。\(c(C)=2n-2, c(C^\star)=n\) となるので、\(\frac{c(C^\star)}{c(C)}=\frac{1}{2-2/n} \rightarrow \frac{1}{2}\ (n\to \infty)\)となる。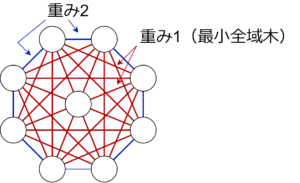
1.5近似：クリストフィードのアルゴリズム
メトリックTSPの1.5近似として、次のクリストフィードのアルゴリズム（Christofides’ algorithm）がある[1]。
- \(G\) の最小全域木 \(T\) を構築する。
- \(T\) の奇点（次数が奇数）全体が誘導する \(G\) の部分グラフで、重み最小の完全マッチング \(M\) を構築する。握手補題より奇点は偶数個存在するので、\(M\) は必ず存在する。
- グラフ \(T+M\) は全ての頂点の次数が偶数なので、オイラー回路 \(C’\) が構築できる。
- \(C’\) の頂点を順番に走査し、出現した同一頂点を２つ目以降削除して、1.5近似のハミルトン閉路 \(C\) を得る。例えば、-x-y-z- というパスが \(C’\) に含まれていて、y がすでに出現していたなら y を削除して -x-z- とする。
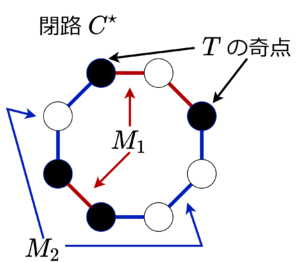
\(c(M_1),c(M_2) \leq c(M)\) なので
\begin{align}
c(C^\star)&= c(M_1) + c(M_2) \\
& \leq 2c(M)
\end{align}が成り立つ。よって \(M+T\) のオイラー回路から得られたハミルトン閉路 \(C\) は
\begin{align}
c(C) &\leq c(M)+c(T) \\
&=\frac{1}{2}c(C^\star)+c(C^\star) \\
&=\frac{3}{2}c(C^\star)
\end{align}
つまり$$\frac{c(C)}{c(C^\star)} \leq 1.5 $$となる。
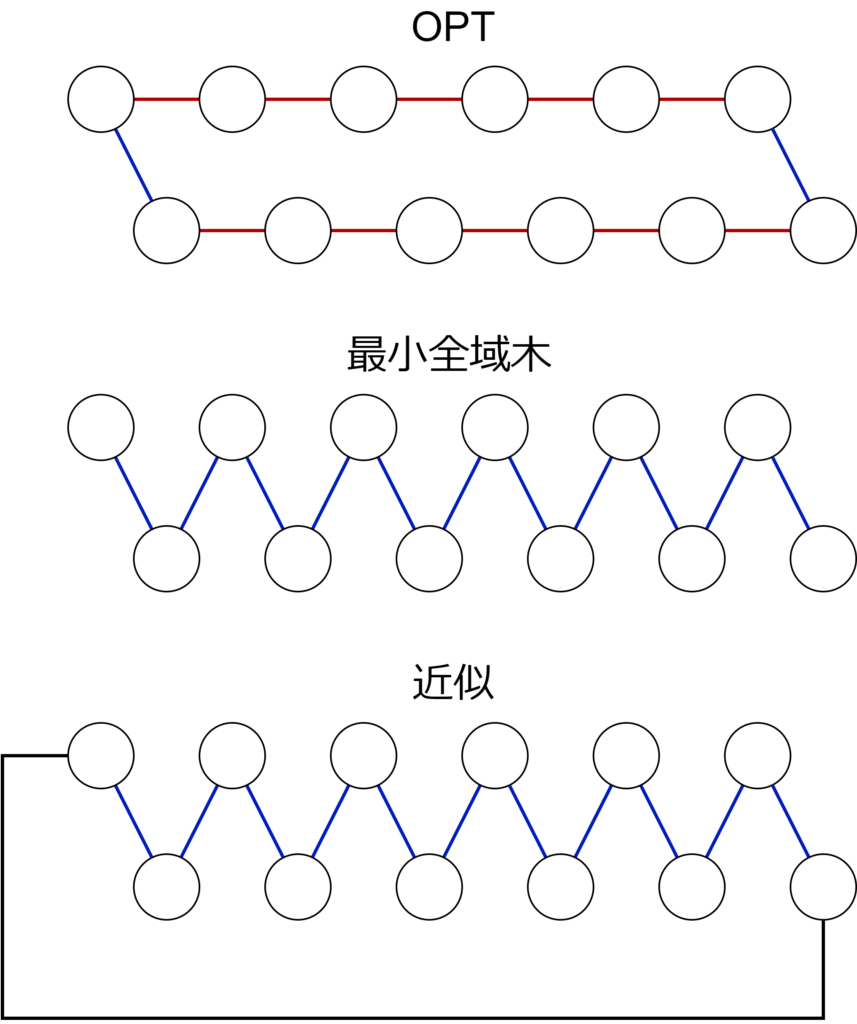
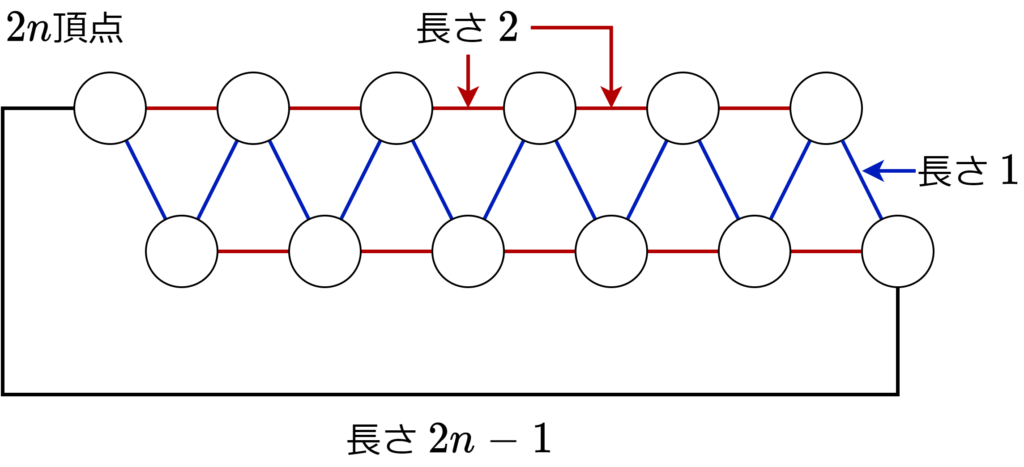タイトな近似例は上図。最適な閉路（OPT)、最小全域木、得られる近似は下図。\(c(C)=3n-2, c(C^\star)=2n-2\) となるので、\(\frac{c(C^\star)}{c(C)}=\frac{2n-2}{3n-2} \rightarrow \frac{2}{3}\ (n\to \infty)\)となる。
参考文献
- Christofides, Nicos. Worst-case analysis of a new heuristic for the travelling salesman problem. Carnegie-Mellon Univ Pittsburgh Pa Management Sciences Research Group, 1976.
Comments