Graph Theory (Diestel) の演習問題4 (Chapter2) が面白いと思ったので取り上げてみます。
問題:無向グラフ \(G\) 上で二人の男女がひとつの駒を使った陣取りゲームをしている。男が先手、女が後手。それぞれのターンでは、駒を未訪問の隣接頂点に動かさなければならない。動かせなくなった方が負け。まだ駒がどの頂点にも置かれていないときは、好きな頂点に駒を置ける。男女は最適に行動するとき、どちらが勝つか。
勝利条件は次の通り。
完全マッチング \(M\) が存在 \(\Leftrightarrow\) 後手の勝ち。
証明:
\(\Rightarrow\) : 後手は完全マッチングの辺に沿って動かすと必勝。
\(\Leftarrow\) : 対偶を示します。最大マッチング \(M’\) を一つ固定し、\(M’\) に含まれない頂点 \(v\) から先手が始めます。先手は \(M’\) の辺に沿って動かすと必勝です。\(M’\) の辺に沿って動かせないと先手の負けですが、そのとき交互増加道が存在するので、最大マッチングに矛盾。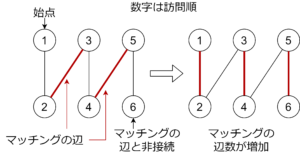
始点が固定されている場合
こんなツイートが届きました。
始点が固定されている場合もオススメです
— 熨斗袋 (@noshi91) September 14, 2021
考えてみましょう……。
問題:無向グラフ \(G\) 上で二人の男女がひとつの駒を使った陣取りゲームをしている。男が先手、女が後手。それぞれのターンでは、駒を未訪問の隣接頂点に動かさなければならない。動かせなくなった方が負け。最初、駒は頂点 \(v\) に置かれている(頂点 \(v\) は訪問済みとする)。男女は最適に行動するとき、どちらが勝つか。
勝利条件は次の通り。
始点 \(v\) を含まない最大マッチング \(M\) が存在 \(\Leftrightarrow\) 後手の勝ち
証明
\(\Rightarrow\) : 後手は \(M\) の辺に沿って動かすと必勝。動かせなければ、交互増加道が存在して、最大性に矛盾。
\(\Leftarrow\) : 対偶を示します。最大マッチング \(M’\) に沿って先手は動かすと必勝。動かせなければ、交互道が存在して、\(v\) を含まないマッチングが存在しないことに矛盾。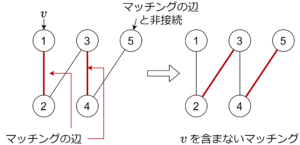
綺麗に解決しましたね。一問目の必勝法は去年の輪読で maspy さんに教えてもらいました。
Comments