有向グラフのMengerの定理（辺ver) は、各辺の容量が１のネットワークにおいて、最大流・最小カット定理を使えば直ちに分かる。

辺ver : 有向から無向へ

辺verの有向グラフでの成立から無向グラフでの成立を導くにあたり、無向辺 \({v, w}\) を有向辺 \((v, w),(w, v)\) に置き換えるだけでは不十分である。なぜか？

有向グラフで辺素なパスが、無向グラフでは辺素とはかぎらないからである。有向グラフでは、\((v, w)\)と\((w, v)\)は辺素だが、無向グラフでは\(\{v,w\}\)と\(\{w,v\}\)は同じ辺だから辺素でない。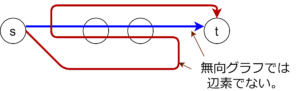

そこでダミー頂点を追加して、\(v → w\) パスと \(w → v\) パスが真ん中の \(↓\) という辺 \(e\) を共有するようにする。\(s, t\) を分離するのに必要な辺数が無向と有向で等しいのはほとんど自明だろう。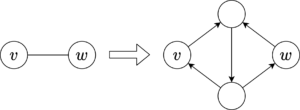

辺verから点verへ

点素の成立から辺素の成立を言うには、線グラフを考えればいい。

辺素の成立から点素の成立を言うには、\(s, t\) 以外の頂点 \(v\) を、辺の入る頂点 \(v_1\), 出る頂点 \(v_2\) に分割する。\(s, t\) が非隣接なら、\((v_1, v_2)\) の形の辺を削除した方が、少ない辺数で \(s, t\) を分離できる。

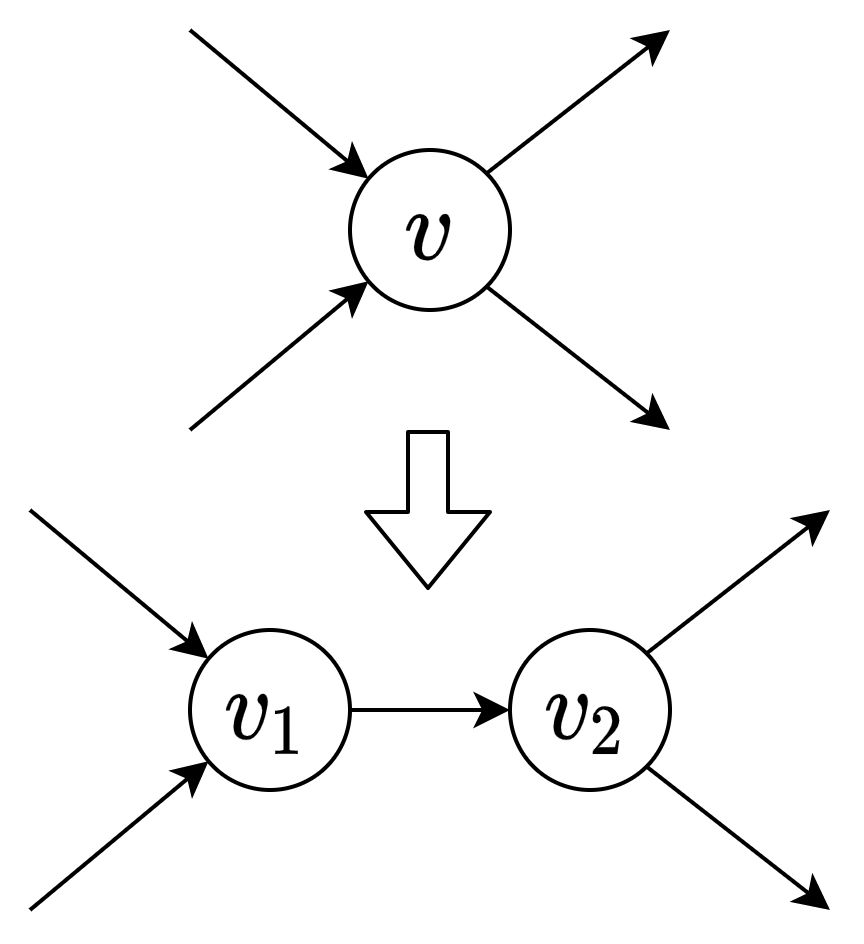
\(v_1\) に入る辺、\(v_2\) から出る辺を削除するよりは、\((v_1, v_2)\) を削除した方が良い。

\((v_1, v_2)\) の辺の削除が元のグラフの頂点 \(v\) の削除に対応している。従って元のグラフの点連結度と、変換後のグラフの辺連結度が同じ。

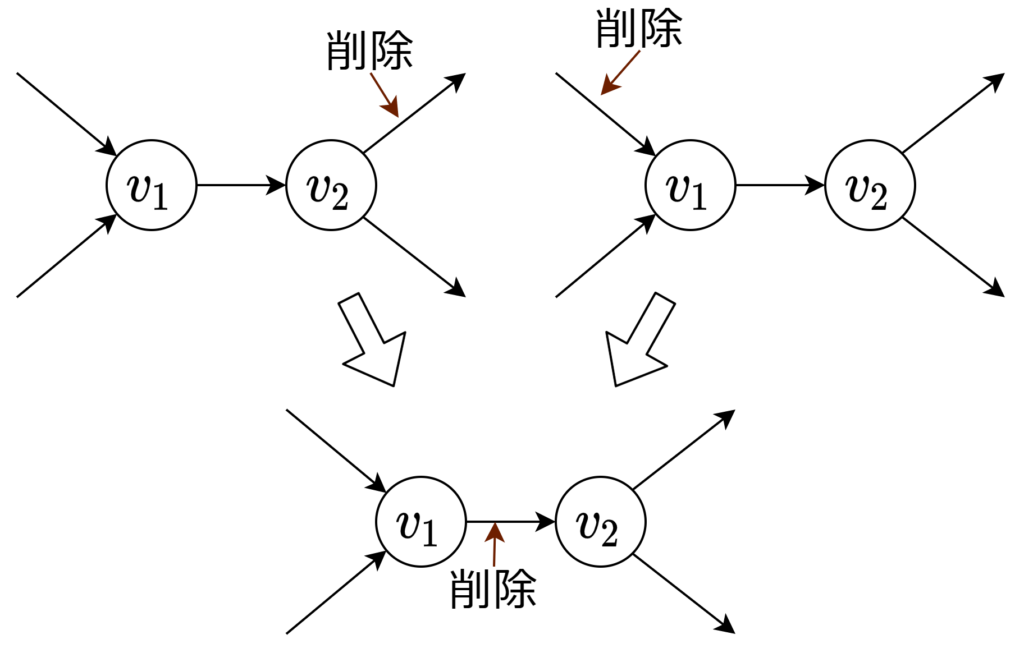
\((s, t)\) の削除は、元の頂点 \(s\) の削除に対応したいため、\(s, t\) を非隣接としている。\(s, t\) が隣接している場合は辺 \((s, t)\) を削除したグラフに対して、帰納法を使えば示せる。