全永続 Queue の一種である銀行家の Queue(Banker’s queue)を解説する。
全永続 Queue とは?
永続データ構造とは、過去のバージョンにアクセス可能なデータ構造のことである。ふつうデータ構造を更新すると、更新元は破壊的に変更されてアクセスできなくなる。しかし、永続データ構造では更新の際に元のデータ構造を全く変更せず、新たに更新後のデータ構造を作成する。永続データ構造のうち、過去のバージョンを更新できるものを全永続、できないものを半永続という。例えるなら、半永続は過去を見る能力、全永続は過去に戻り、パラレルワールドを作る能力(元の世界は不変)である。永続でないデータ構造を短命データ構造という。
この記事で目標とする銀行家の Queue は各操作がならし O(1) の全永続 Queue である。つまり次のような問題を処理するデータ構造である。
- \(Q_i\) := \(Q_{t_i}\).push(\(x_i\))
- Queue \(Q_{t_i}\) の末尾に \(x_i\) を追加した Queue を \(Q_{i}\) とする。
- \(Q_i\) := \(Q_{t_i}\).pop()
- Queue \(Q_{t_i}\) の先頭を削除した Queue を \(Q_{i}\) とする。
- \(Q_{t_i}\).top()
- Queue \(Q_{t_i}\) の先頭を出力せよ。
ただし \(0 \leq t_i < i\) である。
単に永続 Queue と言ったとき、全永続 Queue を指しているものとする。
短命 Queue を 2 個の Stack で作る
銀行家の Queue は 2 本の Stack を用いて構成される。そこでまずは短命な Queue を 2 本の短命な Stack f, r(前方:”f”ront, 末尾:”r”ear)で構成する方法を解説する。次のようにすればよい:
- Queue への push は r への push で表す。
- Queue の pop は f の pop で表す。
- Queue の top は f の top で表す。
ただし、このままでは f が空になると pop と top ができなくなってしまう。そこで pop または top が呼び出されたとき、f が空ならば r の要素の順番を reverse して f に移動する。reverse に必要な計算量は O(|r|) だが、各要素は高々 1 回しか reverse されないから r への push で均すと O(1) になる。従って、この 2 本の Stack による Queue はならし O(1) で各操作ができる。
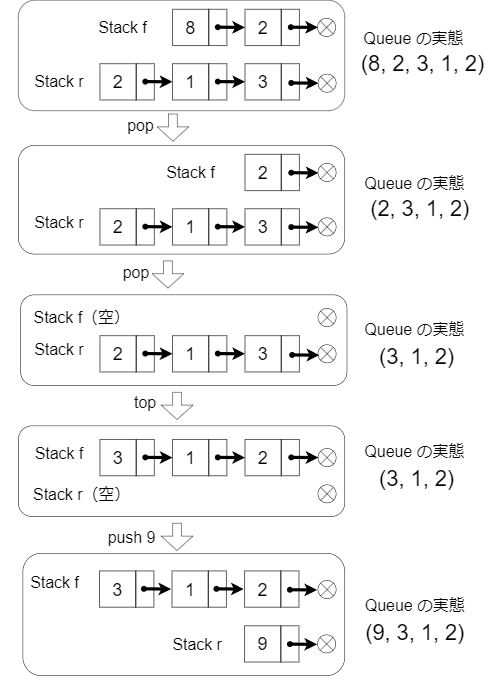 図1:短命 Queue を2つの短命 Stack で構成したときの動作例
図1:短命 Queue を2つの短命 Stack で構成したときの動作例図は 2 つの Stack で Queue を構成した例である。最初 2 つの Stack は f = (8, 2), r = (2, 1, 3) であり、その実態である Queue は f ++ reverse(r) = (8, 2, 3, 1, 2) である(++はリストの連結)。Queue から 2 回 pop する。これはスタック f を 2 回 pop したことと同等である。f が空になる。top を呼び出すと f が空であるから f ← reverse(r), r ← ∅ としてから f の先頭を返す。Queue に 9 を push する。これはスタック r に 9 を push することと同等である。
Java で実装すると次のようになる:
import java.util.Stack;
class Queue {
Stack f = new Stack<>();
Stack r = new Stack<>();
void push(int x) {
r.push(x);
}
int top() {
normalize();
return f.peek();
}
void pop() {
normalize();
f.pop();
}
void normalize() {
if (f.isEmpty()) {
while (!r.isEmpty()) f.push(r.pop());
}
}
}
Stack を永続化する
短命 Queue は 2 個の短命 Stack で作れた。銀行家の Queue はこの 2 個の Stack を永続化することで永続性を獲得する。そこでまずは、Stack を永続化する方法を解説する。
永続 Stack とは次のような問題を処理するデータ構造である。各操作を O(1) にしたい。
- \(S_i\) := \(S_{t_i}\).push(\(x_i\))
- Stack \(S_{t_i}\) の先頭に \(x_i\) を追加した Stack を \(S_{i}\) とする。
- \(S_i\) := \(S_{t_i}\).pop()
- Stack \(S_{t_i}\) の先頭を削除した Stack を \(S_{i}\) とする。
- \(S_{t_i}\).top()
- Stack \(S_{t_i}\) の先頭を出力せよ。
ただし \(0 \leq t_i < i\) である。
各 \(S_i\) が個別にスタックの全要素を持つと push に \(\Theta(N)\) 掛かってしまう。そこで、各 \(S_i\) は Stack の先頭の値と \(S_i\).pop() へのポインタだけを持つことにする。つまり、pop と push を次のように改造する:
- \(S_i\).pop() は \(S_i\) のポインタの参照先を返す。
- \(S_i\).push(\(x\)) は値 \(x\) と \(S_i\) へのポインタを持つ新たな Stack を返す。
これらは全て O(1) で行える。従って pop, push, top が O(1) でできる永続 Stack ができた。
このとき、 \(S_i\) を頂点、ポインタを有向辺と見なすと \(S_0\) を根とする有向木になっている。Stack が容易に永続化できたのはこのように木構造をなすからである。
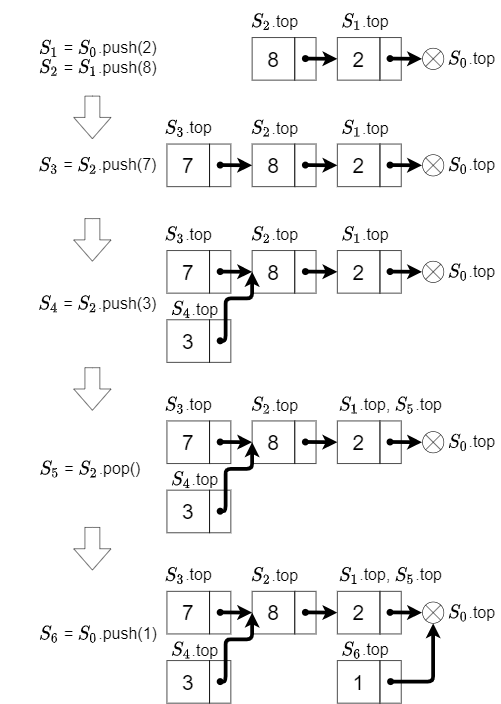
画像は永続 Stack の動作例である。\(S_1\)=\(S_0\).push(2), \(S_2\)=\(S_1\).push(8) とする。\(S_0\) は空のスタックである。\(S_3\)=\(S_2\).push(7) とすると \(S_3\) のポインタは \(S_2\) を参照する。同様に \(S_4\)=\(S_2\).push(3) とすると \(S_4\) のポインタは \(S_2\) を参照する。\(S_5\)=\(S_2\).pop() とすると、\(S_5\) のポインタは \(S_2\) のポインタの参照先 \(S_5\) を指す。\(S_6\)=\(S_0\).push(1) とすると \(S_6\) は \(S_0\) を参照するポインタを持つ。
永続 Stack を Java で実装すると次のようになる:
class PersistentStack {
PersistentStack next = null;
int val;
public PersistentStack(int val, PersistentStack next) {
this.val = val;
this.next = next;
}
// 空の Stack を作る
public PersistentStack() {
}
int top() {
return val;
}
PersistentStack pop() {
return next;
}
PersistentStack push(int v) {
return new PersistentStack(v, this);
}
}
public class Main {
public static void main(String[] args) {
PersistentStack S0 = new PersistentStack();
PersistentStack S1 = S0.push(2);
PersistentStack S2 = S1.push(8);
PersistentStack S3 = S2.push(7);
PersistentStack S4 = S2.push(3);
PersistentStack S5 = S2.pop();
PersistentStack S6 = S0.push(1);
}
}銀行家の Queue
短命 Queue は 2 個の短命 Stack で作れた。前方(front)と後方(rear)の Stack をそれぞれ f, r とする。自然な発想として、短命 Queue を永続化するには短命 Stack f, r を永続化すればよさそうである。しかしそのまま Stack を永続化すると次の2つの厄介事が発生する:
- Queue Q の f が空ならば Q.pop() が繰り返し呼び出されると、その度に reverse(r) を構築する必要がある。
- Queue Q の f が空ならば Q.push(\(x_i\)).pop() が繰り返し呼び出されると、その度に reverse(r ++ (\(x_i\))) を構築する必要がある(r ++ (\(x_i\)) はリスト r とリスト (\(x_i\)) を連結したリスト)。ただし、\(x_i\) は呼び出しの度に異なるとする。
reverse(r) の構築には O(|r|) だけ掛かる。つまり1,2のどちらも、 r の各要素の r への push の計算量では reverse の計算量をならしきれない。
この2つの厄介事は一見同じ問題に見えるが、別個に対処法を打つ必要がある。なぜなら、図2のように永続 Stack を根付き木上のパスと捉えたとき、厄介事1は同一パスについての、厄介事2は分岐した複数のパスについての問題だからである。簡単のために問題2の分岐後のパスの長さは 1(リスト (\(x_i\)) の長さは 1 )としたが、分岐後のパスがもっと長い場合でも厄介事になる。
厄介事1は reverse(r) の構築結果をメモ化し、二度目以降はその結果を参照するだけの O(1) にすることで対処する。1度目の呼び出しの reverse は厄介事2のせいでならし O(1) にできるかは分からない。しかし、二度目以降の呼び出しはメモ化で O(1) にできる。
厄介事2は、reverse(r) を f に追加するタイミングを |r|=|f|+1 のときに早め、更に reverse と ++ の実行を必要になるまで遅延させることで対処する(|f|=|r|にしないのは、f と r が空の場合にこの条件を満たしてしまうからである)。reverse(r) を f に追加してから、Queue を |reverse(r)| 回 pop するまで reverse(r) の具体的な構造は必要ない(無在庫販売のようなものである)。すなわち |reverse(r)| 回 pop する間、revese(r) の実行は保留する。この |reverse(r)| 回の pop の計算量で一度目の呼び出しの reverse(r) の計算量をならし O(1) にできる。
reverse(r) の後ろに別のリストの reverse が連なり、|reverse(r)| 回の pop の計算量が後ろに連なる reverse のならしに使われる場合もある。しかし、この場合も pop のならしコストの定数倍を大きく取っておけば問題ない。
++ の計算量を解析する。停止計算 (x ++ y) を 1 step 進めた停止計算は x.top() :: (x.pop() ++ y) とする。(x :: y は x→y の単方向リスト)。停止計算 S=((((a₁ ++ a₂) ++ a₃) ++ a₄) … ++ aₙ) について、S.pop() を計算するには括弧の入れ子を再帰して一番内に辿り着く必要がある。そこで、停止計算 (x ++ y) を 1 step 進めて x.top() :: (x.pop() ++ y) としたとき :: をメモ化する。二度目以降の S.pop() の呼び出しでは x.pop() ++ y を参照するだけでよい。再帰の深さが S の \(a_i\) の位置以上になるのは高々 \(\sum_{k=1}^i |a_i| \leq 2 |a_i|\) 回である。末尾の stack r に対する \(a_i\) の各要素の push でならせば O(1) となる。pop() について解析したが、top() でも全く同様にしてならし O(1) が示せる。
以上を組み合わせることで各操作がならし O(1) の永続 Queue になる。この永続 Queue を銀行家の Queue という。
front の Stack は Stack の要素が頂点、++ とポインタが有向辺、reverse が木の葉以外を覆う disjoint なパス、Stack が木上の重なり得るパス、Stack の末端の null ノードが葉だと見て、根付き木と捉える事もできる。根付き木として見た方が、どこをメモ化してるのかが個人的には分かりやすくなると思う(逆に混乱させてしまったらこの部分は忘れてほしい)。
銀行家の Queue を Java で実装すると下のようになる。メモ化というと引数 r に対して計算結果 reverse(r) を覚えておくことを指すことが多い。しかし、ここでのメモ化は引数 r を忘れて、ポインタの参照先を停止計算から計算済みの結果に貼り替えるだけで行っている(PersistentStack pop() の next = next.eval() の部分)。
class PersistentStack {
PersistentStack next = null;
int val;
public PersistentStack(int val, PersistentStack next) {
this.val = val;
this.next = next;
}
public PersistentStack() {
}
int top() {
return val;
}
PersistentStack pop() {
return next != null ? (next = next.eval()) : next;
}
static PersistentStack push(PersistentStack x, int v) {
return new PersistentStack(v, x);
}
static PersistentStack concat(PersistentStack x, PersistentStack y) {
if (x == null) return y.eval();
else return new PersistentStack(x.val, new PersistentStack() {
@Override
PersistentStack eval() {
return PersistentStack.concat(x.pop(), y);
}
});
}
static PersistentStack reverse(PersistentStack head) {
return new PersistentStack () {
@Override
PersistentStack eval() {
PersistentStack ret = null;
for (PersistentStack x=head;x!=null;x=x.pop()) {
ret=PersistentStack.push(ret, x.top());
}
return ret;
}
};
}
synchronized PersistentStack eval() {
return this;
}
}
class PersistentQueue {
int fsize = 0;
int rsize = 0;
PersistentStack f = null;
PersistentStack r = null;
public PersistentQueue(PersistentStack f, int fsize, PersistentStack r, int rsize) {
this.fsize = fsize;
this.rsize = rsize;
this.f = f;
this.r = r;
}
public PersistentQueue() {
}
boolean isEmpty() {
return fsize == 0;
}
int top() {
return f.top();
}
PersistentQueue push(int x) {
return new PersistentQueue(f, fsize, PersistentStack.push(r, x), rsize+1).normalize();
}
PersistentQueue pop() {
return new PersistentQueue(f.pop(), fsize-1, r, rsize).normalize();
}
PersistentQueue normalize() {
if (fsize >= rsize) return this;
else {
return new PersistentQueue(PersistentStack.concat(f, PersistentStack.reverse(r)), fsize+rsize, null, 0);
}
}
}演習問題
参考文献
- 純粋関数型データ構造(日本語)
、(英語)
- 日本語書籍の 2.1 リスト, 4章ストリーム, 3.4 銀行家法, 付録A を参考にした。永続データ構造の荒野を共に駆け巡ってくれる本。
- 20分でわかる Purely Functional Data Structures(k.inaba氏)
- 参考文献1の翻訳者による解説。
- あなたの庭に永続データ構造を飾りませんか?(熨斗袋氏)
- 永続 Stack の丁寧な解説(C++の実装あり)。
- 銀行家の Queue の C++ による実装(熨斗袋氏)
- 銀行家の Queue の Java による実装(Aliaksandr Radzivanovich 氏)
- ※reverse された列同士の結合が切れているので計算量は壊れていると思う。
Comments