最大独立集合問題はNP困難であるため[1]、多項式の計算量で解くことはできないだろうと信じられている。しかし、指数の底を改善することで速度を大幅に向上したアルゴリズムがある。

最大独立集合問題とは

まず、用語を定義しておく。隣接する頂点が存在しない頂点集合 \(S\subseteq V(G)\) を \(G\) の独立集合という。独立集合のうち、頂点数最大のものを最大独立集合という。最大独立集合問題とは「最大独立集合を一つ求めよ」あるいは「最大独立集合の大きさ \(\alpha(G)\) を求めよ」という問題である。どちらであるかは文脈に依存する。

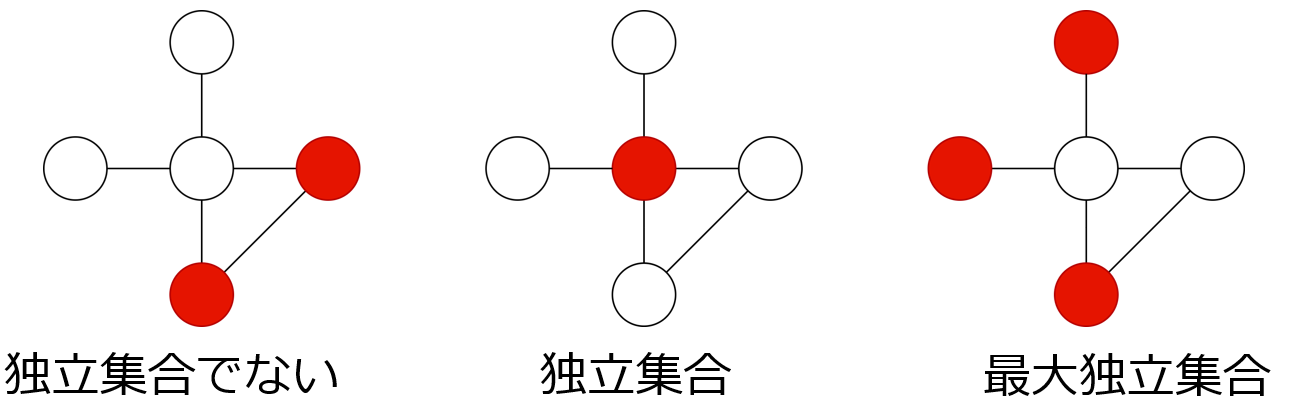
例を挙げる。下の３つ図のそれぞれについて、赤頂点を要素とする集合を考える。左の図は互いに隣接する頂点が存在するので独立集合でない。真ん中の図は互いに隣接する頂点が存在しないので独立集合である。サイズ 4 以上の独立集合は存在しないので、右の図は最大独立集合である。

\(n\) 頂点のグラフの最大独立集合を求めるのに必要な、多項式部分を無視した計算量を \(T(n)\) と置く（どのアルゴリズムを用いるかは文脈に依存）。また、指数関数 \(f(n)\) に対して多項式部分を無視した計算量の表記 \(O^*(f(n)):=f(n)n^{O(1)}\) を使う。

極大独立集合の個数

頂点集合の部分集合の全てについて調べることで独立集合を列挙すれば計算量は \(O^*(2^n)\) である（\(n\) は頂点数）。しかしこの解法は独立集合以外も調べており、効率が悪い。そもそも極大独立集合はどのぐらい存在するのか。極大独立集合の個数については次の定理が知られている。

極大独立集合の個数が最大になるのは \(K^3\) を可能な限り作った後、残りの頂点で \(K^2\) を作った場合であることが知られている（上の証明と同じ方針で地道に場合分けすると示せる[2]）。\(K^2\) は 2 個以下になる。極大独立集合は各 \(K^3\) 、\(K^2\) から頂点を 1 つずつ選ぶ。

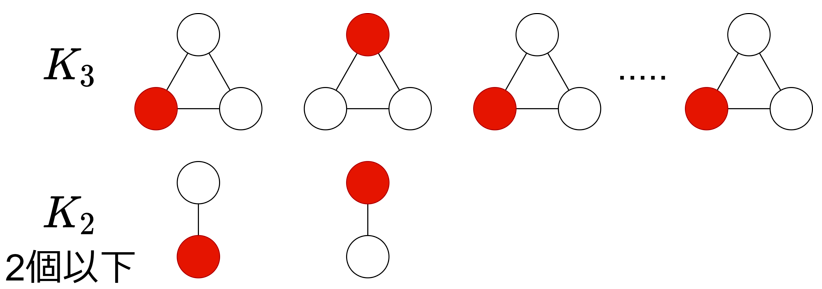
特に \(n = 0 \pmod 3\) のとき \(A(n)=3^{n/3}\) となり等号が成立する。証明はそのまま極大独立集合を列挙するアルゴリズムにできて \(\Theta^*(3^{n/3})=\Theta^*(2^{0.528.. n})\) だから部分集合全列挙 \(\Theta^*(2^n)\) と比べれば高速である。\(\Theta^*(3^{n/3})\) から高速化するには、一部の極大独立集合だけを調べる必要がある。次の節からそのような手法を見ていく。

探索アルゴリズム：mis1

頂点 v を含む独立集合の最大サイズは \(1+\alpha(G-N_G[v])\) 、頂点 v を含まない独立集合の最大サイズは \(\alpha(G-v)\) である。従って、$$\alpha(G)=\max(1+\alpha(G-N_G[v]),\alpha(G-v)) \tag{1}$$である。この漸化式に従って最大独立集合のサイズを計算すると、\(G\) が孤立頂点のみからなるときに \(O^*(2^n)\) 掛かってしまう。そこで枝刈りを加える。全ての頂点の次数が 2 以下のグラフはパスとサイクルの集合からなる。このようなグラフは多項式時間で最大独立集合を計算できることに着目しよう。次数 3 以上の頂点が存在する場合のみ上の漸化式に従って分岐する。このとき、\(|N_G[v]| \geq 4\) だから、
\(T(n) \leq T(n-1)+T(n-4)\tag{2}\) が成り立つ。\(x^n=x^{n-1}+x^{n-4}\) の唯一の正の解 \(x=2^{0.465..n}\) より \(T(n)=O^*(2^{0.465..n})\) となる。極大独立集合を全列挙する解法 \(O^*(2^{0.528..n})\) より高速である。このアルゴリズムを mis1 と呼ぶことにする。

mis1 の Lower Bound

mis1 の計算量の lower bound を求めたい。各頂点にラベル \(1,2,\ldots,n\) を割り当て、\(|i-j| \leq 3\) を満たす相異なる頂点 \(i,j\) 間に辺を張ったグラフを \(P_n\) とする。

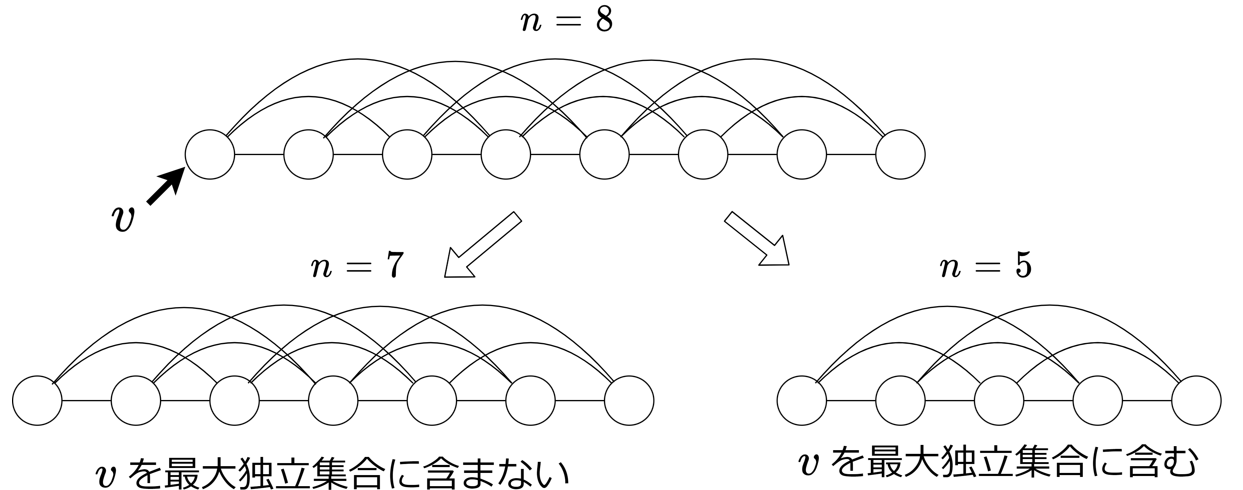
頂点 1 で分岐すると \(P_n\) は \(P_{n-1}\) と \(P_{n-4}\) の部分問題に帰着される。例えば、図は \(P_8\) から \(P_7,P_5\) に分岐した場合である。ここから \(T(n-1)+T(n-4) \leq T(n)\) を得る。これは式(2)の不等号を逆にしたものだから、計算量の上界と下界が一致した事が分かる。つまり \(T(n)=\Theta^*(2^{0.528..n})\) である。この場合は上界と下界が一致したが、一般には最大独立集合問題のアルゴリズムの計算量解析は難しく、上界と下界に開きがあることが多い。

mis2 と Measure & Conquer

mis1 を改造して、次数の大きい頂点 v から順に分岐することにしたアルゴリズムを mis2 と呼ぶことにする。mis1 は mis2 に比べて式(1)の \(G-N_G(v)\) が小さくなるので速そうである。しかし、今までの解析方法では mis1 と mis2 で上からの評価は変化ない。そこで Measure & Conquer [4]と呼ばれる新たな解析手法を用いると、mis2 が mis1 に比べて計算量が改善していることを示せる。

ここまでの計算量解析は \(T(n)=O^*(c^n)\) の形で抑えることにより計算を進めてきた。しかし、この形では次数の小さい頂点が多いほど計算が速くなることが考慮されていない。そこで、次数 \(i\) の頂点の個数を \(n_i\) として \(T(n_0,n_1,\ldots,n_{n-1})=O^*(c^{w_0n_0+w_1n_1+\ldots+w_{n-1}n_{n-1}})\) で抑えることにより計算を進める。このように変数を増やす計算量解析を Measure & Conquerと呼ぶ。

\(w_0=0, w_1=0.4, w_2=0.8, w_3=w_4=\ldots=1\) として \(c\) を求めよう。適切な重み \(w_i\) ではなく、計算しやすそうな \(w_i\) を選んだ。\(h=\sum n_i w_i\) と置く。

1. 次数 4 以上の頂点で分岐したとき
   $$c^h \leq c^{h-1} + c^{h-5}$$である。
2. 次数 3 の頂点 v で分岐したとき、次数 3 の隣接頂点が \(k\) \((k \leq 3)\) 個あるとすると
   $$c^h \leq c^{h-1-0.2k-0.4(3-k)} + c^{h-1-k-0.4(3-k)}$$である。

(i), (ii) の不等式を満たす最小の \(c>0\) を求めると、\(T(n)=O^*(2^{0.454..n})\) となり、\(c^n\) で評価したときの \(O^*(2^{0.465..n})\) から評価は改善される。次数 3 以上の頂点からランダムに分岐したときに比べて、次数の大きい頂点から順に分岐したときの方が計算量が改善されることが分かった。

指数空間アルゴリズムの設計 ~メモ化再帰~

アルゴリズム mis1, mis2 は空間計算量が多項式であった。ここからは mis1 の空間計算量を指数関数にすることで時間計算量を削減する。式(1) \(\alpha(G)=\max(1+\alpha(G-N_G[v]), \alpha(G-v))\) に従って再帰的に分岐したときのグラフは元のグラフ \(G\) の誘導部分グラフである。従って頂点集合を引数として計算結果をメモ化できる。\(\alpha n\) \((\alpha<1/2)\) 頂点以下になったところでメモ化することにする[3]。計算量は「\(\alpha n\) 頂点以下誘導部分グラフへの帰着」と「メモ化」の 2 つの計算量の max である。従って、この 2 つの計算量が同サイズになる \(\alpha\) が最適である。\(\alpha n\) 頂点以下の誘導部分グラフの個数は \(\sum_{i=0}^{\alpha n} {n \choose i} \leq n {n \choose \alpha n}\) である。Stirling の近似 \(n!=O^*((n/e)^n)\) により
$$O^*\left(n {n \choose \alpha n}\right) = O^*\left(\frac{1}{(1-\alpha)^{(1-\alpha)n}\alpha^{\alpha n}}\right) \tag{3}$$を得る。mis1 により \(\alpha n\) 頂点以下誘導部分グラフに帰着するのに必要な時間計算量は \(O^*(2^{0.465..n(1-\alpha)})\) であった。この計算量が式(3) と同サイズになるのは \(\alpha≒0.0869\) のときである。このとき全体で \(O^*(2^{0.426n})\) となる。メモ化を使うことで時間計算量が削減できた。

演習問題

• yosupo judge. Maximum Independent Set.（40頂点）
• yukicoder No.382（121頂点）
• CODE THANKS FESTIVAL 2017 : G – Mixture Drug（40頂点）
  • 最大クリーク問題だが、補グラフを取ると最大独立集合問題になる。

最小頂点被覆との関係

最大独立集合の補集合が最小頂点被覆になる。また、最小頂点被覆の補集合が最大独立集合になる。

二部グラフの最大独立集合

二部グラフ G の最大独立集合は次の様にして、多項式時間で求まる（燃やす埋めるで示してもよい）。

最小頂点被覆の補集合は最大独立集合であるから、最小頂点被覆を求めれば良い。二部グラフの各部集合に超頂点 s, t を接続したグラフを考える。二部グラフの最小頂点被覆は、s, t の最小分離頂点集合（s, t を非連結にするために除く最小の頂点集合）に等しい。

二部グラフでは、互いに内素なs-tパスであることと、互いに辺素なs-tパスであることが同値なので、Mengerの定理より s, t の最小分離頂点集合（s, t を非連結にするために除く最小の頂点集合）の大きさは、最小カットの大きさに等しい。最小カット問題は最大流で多項式時間で解ける。

また、最小分離頂点集合の構築は、最小カットの構築に帰着できる(解説)。

弦グラフと平面グラフの最大独立集合

弦グラフと平面グラフの最大独立集合は多項式時間で求まる。別記事で解説予定。

比較可能グラフの最大独立集合

独立集合は反鎖であるので、フローにより求まる。

参考文献

1. Karp, Richard M. “Reducibility among combinatorial problems. ” Complexity of computer computations. Springer, Boston, MA, 1972. 85-103.
   • 最大独立集合問題はNP困難である。
2. Wood, David R. “On the number of maximal independent sets in a graph.” arXiv preprint arXiv:1104.1243 (2011).
   • 極大独立集合の個数の不等式を参考にした。
3. Robson, John Michael. “Algorithms for maximum independent sets.” Journal of Algorithms 7.3 (1986): 425-440.
4. Fomin, Fedor V., Fabrizio Grandoni, and Dieter Kratsch. “Measure and conquer: a simple O (2^0.288 n) independent set algorithm.” Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm. Society for Industrial and Applied Mathematics, 2006.
   • Measure & Conquer を参考にした。
5. Spring School on Fixed Parameter and Exact Algorithms
6. “指数時間アルゴリズム”（wata）