頂点数 \(N\), 辺数 \(M\) の有向グラフ \(G\) の最小全域有向木を \(O(NM)\) で求める Edmonds のアルゴリズムを前の記事で扱いました。今回は、Gabow, Galil, Spencer, Tarjan による、\(O(M+N\log(N))\) への高速化を行います。

DFSで逐次更新：\(O(M\log(N))\)

重み∞の辺を \(O(N)\) 個追加することで、最小全域木を変化させることなく、\(G\) を強連結にできるので、強連結と仮定しても一般性を失いません。

前回のなもり森を、始点はどこでもいいので DFS しながら、構築していきます。閉路ができると縮約するので、常にパスになっています。パスの頂点を順に \(v_1, v_2, \ldots, v_k\) とします。\((v_i,v_{i+1})\) は、\(v_i\) に入る重み最小の辺です。\(v_k\) に入る重み最小の辺が \((w, v_k)\) とします。\(w\) がパスに含まれなければ \(v_{k+1}:=w\) としてDFSを続けます。\(w\) がすでにパスに含まれていて \(w = v_j\) となる \(j\) があるとします。下図では \(k=5,j=3\) です。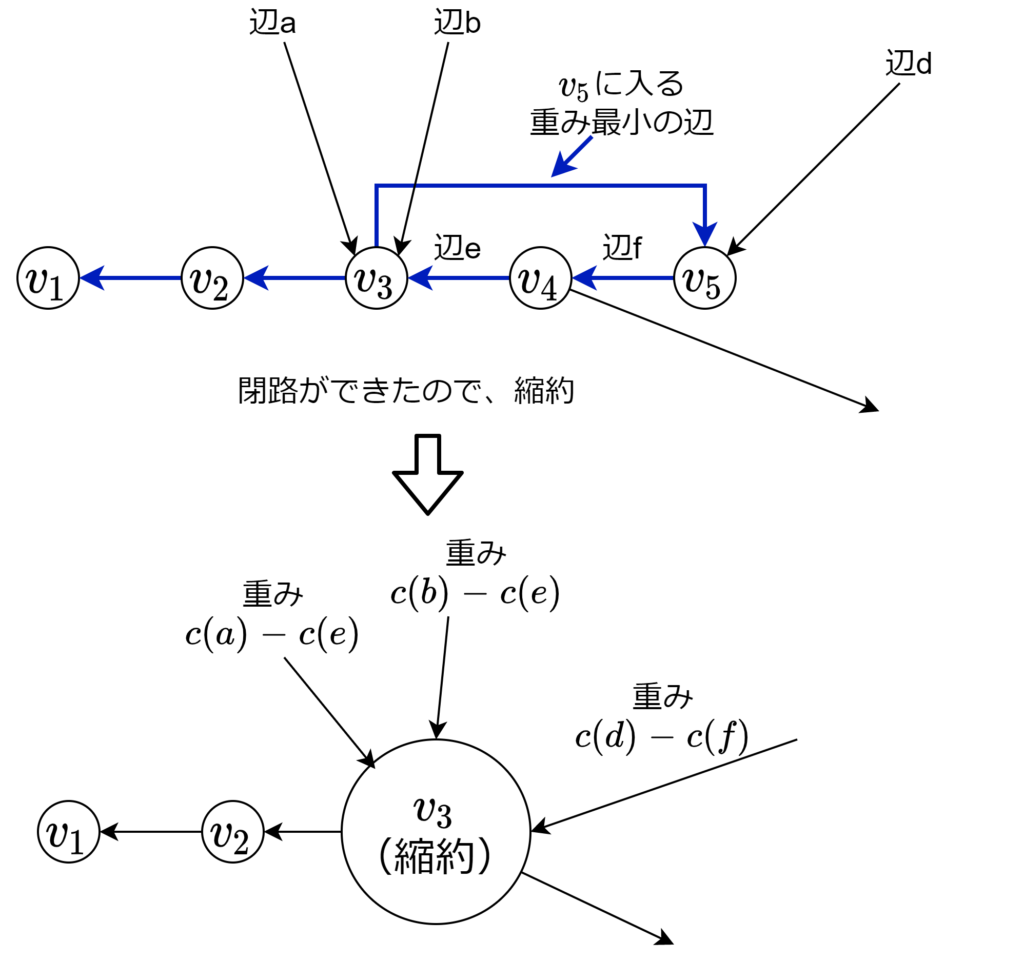このとき、頂点 \(v_j, v_{j+1}, \ldots, v_k\) からなる閉路ができます。前回の議論より、一辺を除いた閉路の辺を含む最小全域木が存在するので、これらの頂点を縮約し、外から閉路の頂点 \(v_l\) (\(j \leq l \leq k\)) に入っていた辺の重みを \(c((v_l, v_{l+1}))\) だけ減算します。これは選ばれなかった辺の重み分です。そして、縮約した頂点から、DFSを再開します。強連結なので、入る辺が見つからないのはグラフが一頂点からなるときであり、計算終了。この状態になったら、計算を逆戻しすれば、最小全域有向木が成り立ちます。

計算量は \(O(NM)\) のままであり、改善されていませんが、実装は簡単になっていると思います。

パス末尾の \(v_k\) に入る重み最小の辺を高速に取得するために、各頂点ごとに、入る辺をヒープ（キーは重み）で管理します。閉路の頂点 \(v_j,v_{j+1},\ldots,v_k\) を縮約するときには、それぞれの頂点のヒープを融合すればよいです。二項ヒープだと \(O(\log(N))\)、フィボナッチヒープだと \(O(1)\) でできます。計算量の悪化を許容すれば、weighted-union rule （小さいヒープを大きいヒープに融合）でヒープの要素を一つずつ移動すれば、ならし \(O(\log(N)^2)\) です。融合の際に、頂点 \(v_l\) (\(j \leq l \leq k\)) のヒープは、要素の重みを全て \(c((v_l,v_{l+1}))\) だけ引く必要があります。これは、縮約した頂点を Union Find で管理し、各頂点に入る辺の減算の和がその頂点から根までのパスの重みになるようにすればよいです。あるいは、減算をヒープの親から遅延伝番すればよいです（こちらの方法は次の高速化では使えなくなります）。

融合は \(N-1\) 回行うので、weighted-union rule、二項ヒープ、フィボナッチヒープ、それぞれ融合の計算量は全体で、\(O(N \log(N)^2)\)、\(O(N\log(N))\)、\(O(N)\) です。

閉路を縮約したとき、weighted-union rule で要素を一つずつ移動したならば自己辺（縮約前は閉路の弦）をその時に取り除けます。一方、二項ヒープやフィボナッチヒープの融合は、ヒープを他方のヒープに部分木としてそのまま移植するので、自己辺が取り除けません。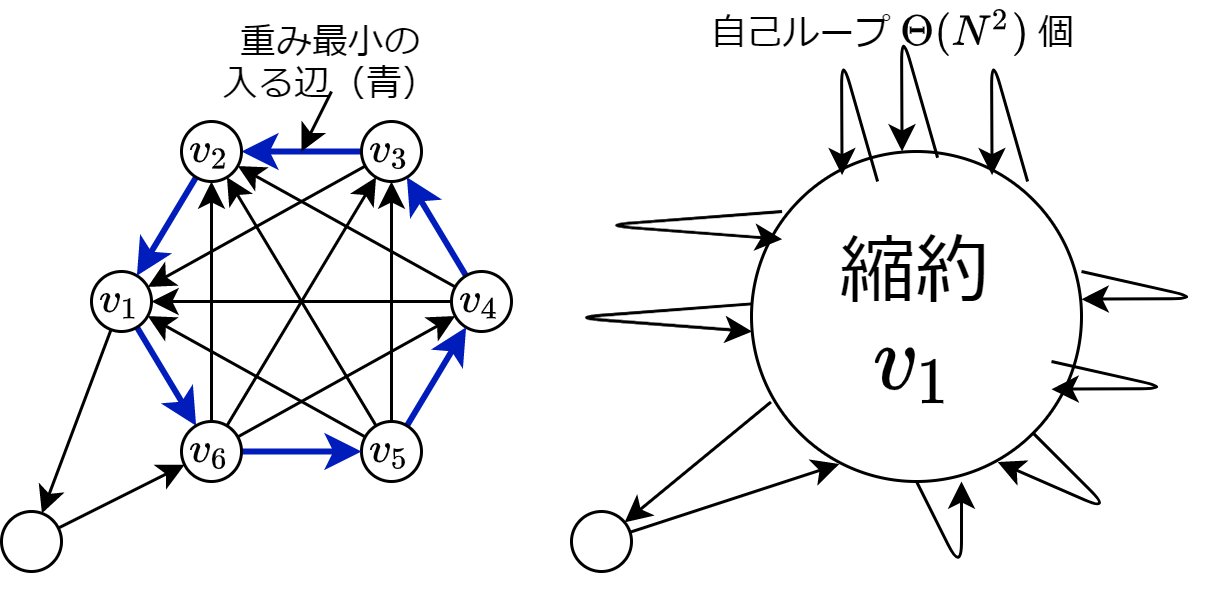従って、パス末尾の頂点に入る、自己辺以外の最小の辺をヒープから得るまで \(O(M)\) 回、delete-min する必要があります。delete-min は二項ヒープ・フィボナッチヒープどちらも \(O(\log(N))\) なので全体の計算量は \(O(M\log(N))\) です。

フィボナッチヒープ

ここから計算量を落とすには、フィボナッチヒープが必要なので、簡単に説明しておきます。これだけでは、全く理解できないと思うので、ほかの方の記事も参照してください。重要なのは decrease-key が \(O(1)\) でできることです。

• insert
  • \(O(1)\)。一頂点の木にして、根のリストに加える。
• delete-min
  • ならし \(O(\log(N))\)。min を削除。その子を根のリストに加える。根の次数が一意になるまで meld を繰り返す。
• decrease-key
  • ならし \(O(1)\)。decrease する頂点を親と切り離し、実際に decrease する。切り離された部分木が、heap-property（親≦子） を満たすまで、根から順に親と子を交換する。decrease したノードを新たに根のリストに加える。フィボナッチヒープの頂点は一度しか子を切り離せないので、decrease-key した頂点の親が違反しているなら、違反した頂点がなくなるまで再帰的に切断を繰り返す。
• meld
  • \(O(1)\)。二つの木を heap-property（親≦子）を満たすように、根の間に辺を繋いで一つの木にする。

フィボナッチヒープ：\(O(M+N\log(N))\)

フィボナッチヒープを用いて、全ヒープの総要素数を \(O(N)\) に保つことで、計算量を \(O(M+N\log(N))\) にしたいです。最小要素を取り出すのは、パス末尾の頂点だけなので、それ以外のヒープは不完全で構いません。そこで、各頂点 \(x\) について、パスに入る辺 \((x, v_i)\) のうち、終点が最もパス末尾に近いもののみを（どこかの）ヒープに入れ、終点がパス末尾 \(i=k\) のとき、その辺は \(v_k\) のヒープにあること（☆）にします。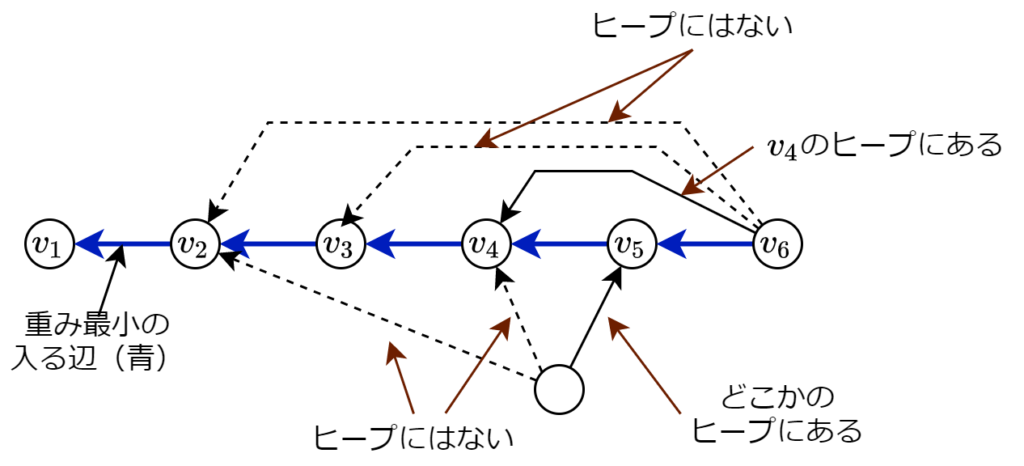また、ヒープの要素は、「その頂点に入る辺（キーは重み）」ではなく、「その頂点に入る辺の始点（キーは重み）」の形で持ちます。キーの重みは「減算前の辺の重み ＋ Union Find の重み」として、必要なときだけ動的に計算します。

以上の状態を保つことで、パス末尾のヒープには必要な要素が全て含まれ、縮約した閉路の弦も全ヒープで \(O(N)\) 個しかありません。

パスに含まれない頂点のヒープは空です。新たにパス末尾になったら、入る辺を全て自身のヒープ \(h_1\) に追加します。このとき、追加された始点 \(x\) がほかのヒープ \(h_2\) にも含まれる場合、☆の条件が壊れてしまいます。そこで、\(h_1\) の \(x\) を根とする部分木を（decrease-key 同様に）切り離して、\(h_2\) の根のリストに加えます。\(h_2\) に移植された \(x\) に対して delete-min が作用したときは、\(x\) と \(h_2\) の子を切り離して \(h_1\) の根のリストに加えます（この時には、\(x\) に \(h_2\) 以外の子が含まれているかもしれません）。

パスの各頂点 \(v_i\) について、ヒープに含まれない入る辺を連結リスト \(L_i\) で管理します。閉路の縮約でヒープを融合したとき、リストの辺の方が重みが小さいなら、decrease-key で帳尻を合わせます。縮約後はリストを空にします。

ヒープの融合によって、別のヒープから移植されてきた部分木の根と子で heap-property （親のキー≧子のキー）が永遠に修復されないままにならないでしょうか？　子に decrease-key したときは、親と子が切り離されるので heap-property は関係ありません。別のヒープから移植されてきたときに、確かに親のキーは変わりますが、移植前のキーが \(L_i\) に保管されるので、結局、閉路の縮約でヒープを融合したときの親の decrease-key で帳尻が合います。

decrease-key が \(O(M)\) 回、delete-min が \(O(N)\) 回、insert が \(O(M)\) 回なので、全体で \(O(M + N \log(N))\) 時間です。

Union Find のオーバーヘッドは掛かりません。これは \(\Omega(N\log(N))\) 回 find ( union 内部のそれを含む）すると、ならし \(O(1)\) になるからです。経路圧縮を無視した仮想的な木の高さが \(O(\log(N))\) になることに起因しています。

参考文献

• 最小全域有向木（m log n）（joisinoさん）
• Gabow, Harold N., et al. “Efficient algorithms for finding minimum spanning trees in undirected and directed graphs.” Combinatorica 6.2 (1986): 109-122.