カット・サイクル空間の基底

グラフ \(G\) の辺集合 \(E(G)\) の部分集合 \(F\) は各辺 \(e \in E(G)\) が辺集合 \(F\) に”含まれるか否か”をベクトルの要素”1/0″に対応させることで \(\mathbb{Z}/2\mathbb{Z}\) ベクトルと一対一対応する。このとき、ベクトルの和は辺集合の対称差と対応づく（下図、要は辺ごとのXOR）。辺集合がなすこのベクトル空間を辺空間と呼ぶ。

この記事では辺空間 \(\mathcal{E}(G)\) の部分空間であるサイクル空間、カット空間の基底について解説する。

サイクル空間 \(\mathcal{C}(G)\) とはサイクルの辺集合全体が生成する \(\mathcal{E}(G)\) の部分空間、またカット空間 \(\mathcal{B}(G)\) とはカットの辺集合全体が生成する \(\mathcal{E}(G)\) の部分空間である。

サイクル空間の元は、サイクルの Disjoint Union になる（非連結になり得ることに注意）。このことは、二つの閉路の XOR が閉路の Disjoint Union になることを思い浮かべれば分かる。また、カット空間の元は（幾つか例外を除き）カットになる。このことは、後述する\(E(v)\) の形の基底で理解できるはずである。

サイクルの Disjoint Union とカットが部分空間として閉じているという点が非常に重要である。サイクル・カット空間の基底を見つけることができれば、サイクルの Disjoint Union やカットの数え上げが容易であることを示唆している。

簡単のために、この記事では辺集合 \(F \in \mathcal{E}(G)\) と \(G\) の部分グラフ \((V,F)\) を区別せずに使う。

基本閉路・基本カット

以下に述べるように、サイクル・カット空間の基底は全域木を用いて簡単に列挙することができる。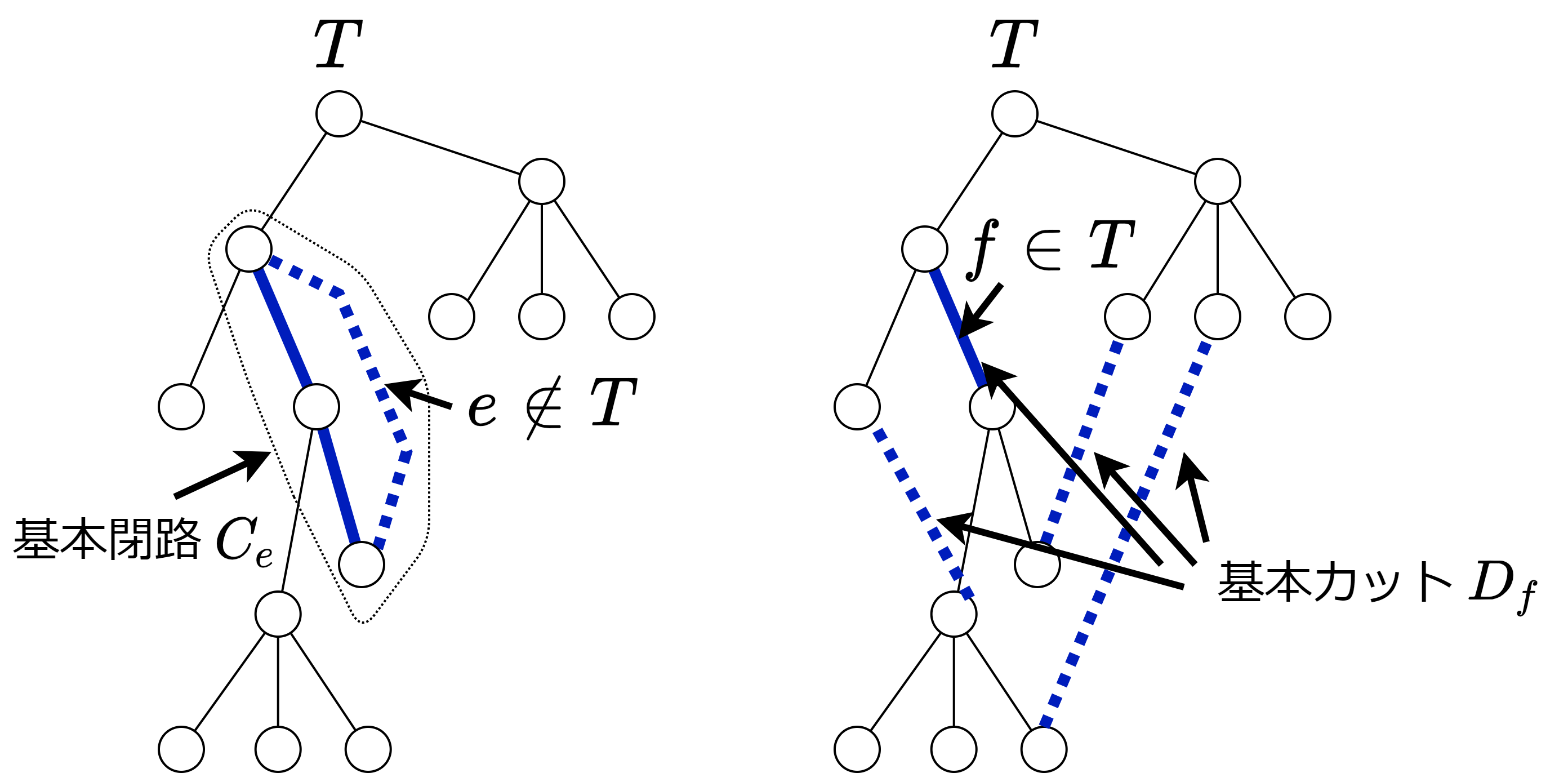適当な全域木 \(T \) を取る。\(T\) に含まれない \(G\) の辺 \(e \in E(G) \setminus E(T)\) を \(T\) に加えた時にできる唯一の閉路 \(C_e\) を \(T\) に関する \(e\) の基本閉路と定義する。また、\(f \in E(T)\) を除いた \(T-f\) の 2 つの連結成分を横切るカット \(D_f\) を \(T\) に関する \(f\) の基本カットと定義する。このとき次の事実が成り立つ。

\(n\) 頂点 \(m\) 辺の連結グラフ \(G\) があり、\(T\) を \(G\) の全域木とする。このとき \(T\) に関する基本閉路と基本カットはそれぞれサイクル空間 \(\mathcal{C}(G)\) とカット空間 \(\mathcal{B}(G)\) の基底をなす。

証明：\(e \notin T\) は基本閉路のうち \(C_e\) のみに含まれる辺であるから、基本閉路は一次独立。同様に \(f \in T\) は基本カットのうち \(D_f\) にのみ含まれる辺であるから基本カットも一次独立。

あとは基本閉路と基本カットがそれぞれサイクル空間とカット空間の全ての元を生成することを示せば良い。サイクル空間の元 \(C+\sum_{e \in C \setminus T} C_e\) は \(T\) の辺のみで構成されるが、そのような回路は存在しない（辺空間での足し算であることに注意）。従って \(C+\sum_{e \in C \setminus T} C_e=\emptyset\) つまり \(C=\sum_{e \in C \setminus T} C_e\) となる。サイクル空間の任意の元 \(C\) が基本閉路で生成できた。同様にカット空間の元 \(D+\sum_{f \in C \cap T} D_f\) は \(T\) の辺を含まないが、そのようなカットは存在しない。従って、\(D=\sum_{f \in D \cap T} D_f\) である。カット空間の任意の元 \(D\) が基本カットで生成できた。

ここから基本閉路・基本カットの数を数えることで \(\mathrm{dim}\ \mathcal{C}(G)=m-(n-1), \mathrm{dim}\ \mathcal{B}(G)=n-1\) が成り立つ。

ところで頂点 \(v\) に接続する辺集合 \(E(v)\) はカットであるが、実はこの形のカット全体はカット空間全体を生成する。一つカットを除いて、\(n-1\) 元にすれば、基底になる。この基底は頂点のXORでカット空間の足し算が捉えられることを表している。基底を求めるだけなら基本カットよりもこちらのほうが求めやすいと思う。Project Selection だと、こちらの方が考えやすい場合がある。

カット \(E(v)\) 全体はカット空間 \(\mathcal{C}(G)\) 全体を生成する

証明：\(E(A,B)=\sum_{v \in A} E(v)\) であるから成立（足し算は辺空間で行っていることに注意）。

演習

ネタバレを避けるために出典は黒塗りにしている。

問題1：カット \(E(v)\) 全体の生成する部分空間に \(E(G)\) が元として含まれるのはどんな場合か。（出典：ARC105F改）

▼ 解説

問題2：\(n\) 頂点 \(m\) 辺の単純無向グラフには回路がいくつ含まれるか。

▼ 解説

問題3：\(n\) 頂点 \(n+15\) 辺以下の単純無向グラフがある。部分グラフとして含まれるサイクルの数を答えるアルゴリズムを構成せよ。また、空でない辺極小なカットの数の場合も考えよ（出典：ICPC2017Asia問題K）

▼ 解説

問題4：\(n\) 頂点 \(m\) 辺の連結グラフが与えられる。各辺に 0, 1 の重みを割り当てる。このとき、「任意の回路の重みが偶数」かつ「全ての辺の重みの和が偶数」であるような重みの割り当て方法がいくつあるか求めよ（\(O(m)\) で解ける）。（出典：HackerRank “Devu and Cycles of a Graph”）

▼ 解説

問題5：\(n\) 頂点 \(m\) 辺の連結グラフが与えられる。各辺 \(e\) には64bit整数の重み \(w_e\) が割り当てられている。\(s=0\) とする。全ての 2 頂点の組 \(u, v\) それぞれについて、\(u, v\) を端点とする歩道の取りうる重みの XOR を \(s\) に加える。s を求めるアルゴリズムを構成せよ。（出典：CodeForces724G）

▼ 解説

問題6：\(n\) 頂点 \(m\) 辺のグラフがある。各辺 \(e\) には64bit整数の重み \(w_e\) が定まっている。カットの重みの XOR を最大化するといくつになるか。

▼ 解説

参考文献

Diestel, Reinhard. “Graph theory. 1997.” Grad. Texts in Math 2 (2016). Capter1.9. (preview)
- この記事では扱わなかった、サイクル空間とカット空間が互いに直交補空間であるという話題が載っています。
[AtCoder 参加感想] 2020/10/12:ARC105 (maspyさんのHP)
- 問題１の原題をカット空間と関連させて解いています（省いてしまいましたが、問題１には続きがあります）。

全域木が上手くハマって面白い。

その他の話題

次数分布が等しい向き付け

無向グラフ \(G\) を向き付けた二つのグラフ \(G_1, G_2\) について、各頂点の入次数・出次数が \(G_1, G_2\) 間で等しいとする。\(G_1, G_2\) で同じ方向に向き付けられている辺を \(G_1\) から削除したグラフを \(G’\) とする。\(G’\) の辺の向きを逆にしても各頂点の入次数・出次数が変わらない。従って、\(G’\) が辺素な有向サイクルの和で書けることと、\(G_1, G_2\) の各頂点の入次数・出次数が等しいことが同値（会長さん、ARC193B）

接続行列

有向グラフ \(G=(V,E)\) と辺重み \(c : E \to \mathbb{F}_2\) が与えられる。任意の \(ij \in E\) について \(x_i + x_j + y_i = c_{ij}\) を満たすような \(x, y : V \to \mathbb{F}_2\) を求めよ（ARC188C）。

\(v \in V\) を一つ取り、\(vw \in E\) かつ \(c_{vw} = 0\) となる \(w\) 全体を \(W\) と置く。すると

\(x_v + x_w + y_v = 0\) for \(w \in W\) という連立方程式は \(x_i = x_j\) for \(i,j \in W\) とある一つの \(w \in W\) を固定して、\(x_v + x_w + y_v = 0\) という式で書ける。\(c_{vw} = 1\) の場合も同様にする。\(x_i=x_j\) または \(x_i \neq x_j\) という形の連立方程式が立ち、これはdfsなどで簡単に解が（存在するなら）求まる。あとは \(x_v + x_w + y_v = 0\) を満たすように \(y\) を決めればよい。