Prüfer コード（Prüfer 列）とは、ラベル付き木を全単射に変換した一種の数列である。ラベル付き木を数えやすい対象に変換でき、木の数え上げに威力を発揮する。

Prüfer コードの定義

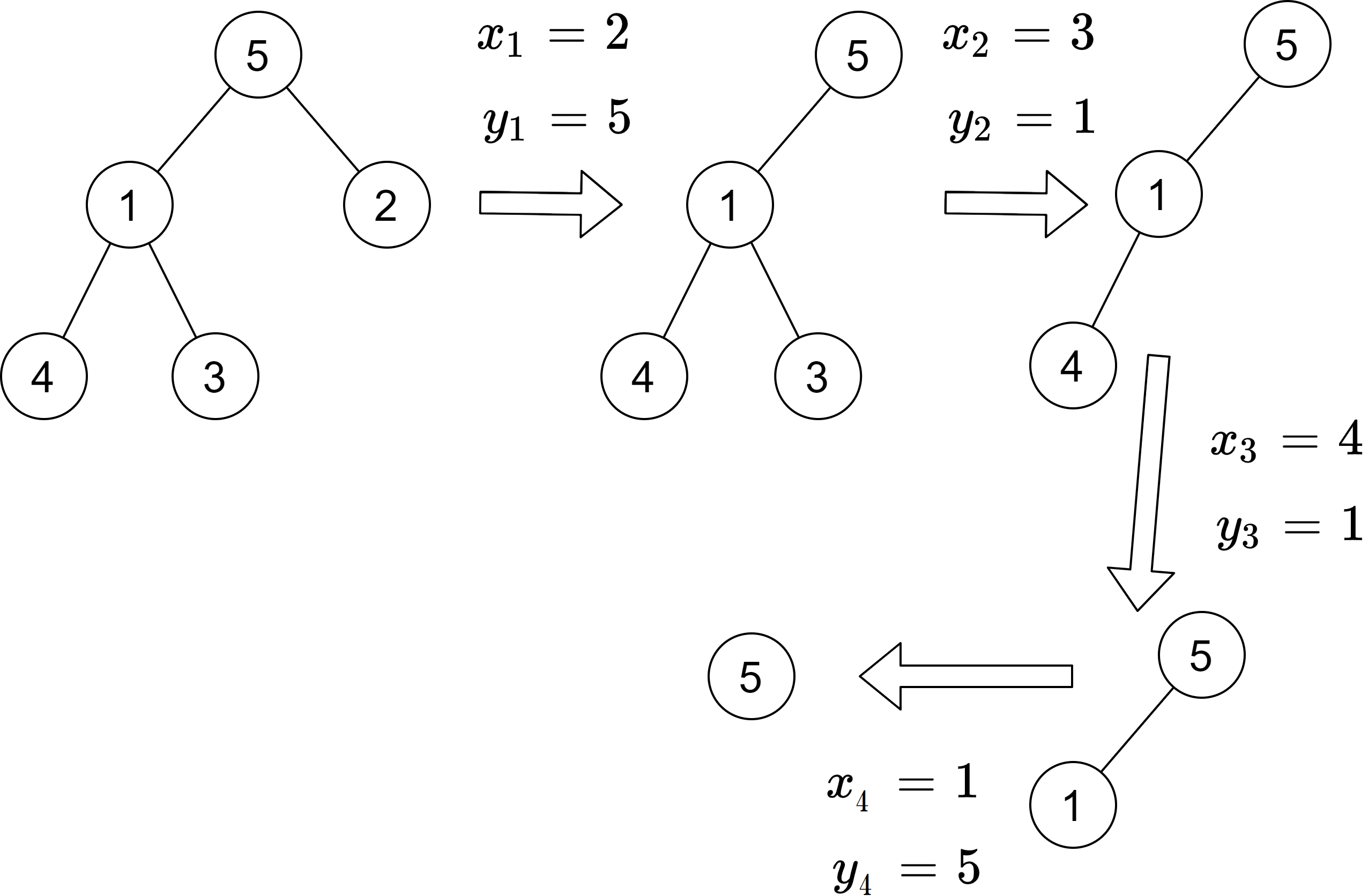
頂点集合 \(V=\{1,2,\ldots,n\}\) からなり、頂点 \(n\) を根とするラベル付き木 \(T\) を考える。木 \(T\) に対する Prüfer code を以下のよう生成される頂点列 \(\mathcal{P}(T)=(y_1,y_2,\ldots,y_{n-2})\) として定義する。

• 以下の操作を \(k=1,2,\ldots,n-1\) について順に行う。
  1. \(T\) のラベル最小の葉を \(x_k\), その親を \(y_k\) とする。
  2. \(T \leftarrow T_k-x_k\)

※ \(y_{n-1}=n\) は Prüfer コードには含まない。

Prüfer コードを作る一例は下図。

Prüfer コードの全単射性

\(n\) 頂点ラベル付き木全体から \(V^{n-2}\) への写像 \(\mathcal{P}\) が全単射であることを示したい。異なる木は異なる Prüfer コードを生成するから \(\mathcal{P}\) は単射である。全射であるには、木をなすように \((y_i)\) から \((x_i)\) が一意に復元できればよい。\(x_1,x_2,\ldots,x_k\) まで復元できたとする。木 \(T_{k+1}\) について、\(x_1,x_2,\ldots,x_k\) はすでに削除された頂点、\(y_{k+1},y_{k+2},\dots,y_{n-1}\) は葉となりえない頂点、その他の頂点は葉である。従って、\(S=\{x_1,x_2,\ldots,x_k\}\cup\{y_{k+1},y_{k+2},\ldots,y_{n-1}\}\) に含まれないラベル最小の頂点が \(x_{k+1}\) として定まる。\(|S| < n\) であるからこのような頂点は必ず取れる。以上より \((y_i)\) から \((x_i)\) が一意に復元できたから、\(\mathcal{P}\) は全単射であることが示された。

Prüfer コードの応用例として最も有名なのは次の定理だろう。

\(\mathcal{P}\) は \(n\) 頂点ラベル付き木全体から \(V^{n-2}\) への全単射であるから、この定理が成り立つ。

次のような数え上げの問題も Prüfer コードによって処理できる。

次数 \(d\) の頂点はちょうど \(d-1\) 回 Prüfer コードに出現するから、\({n-2 \choose d_1-1,d_2-1, \ldots ,d_n-1}\) 通り存在する。

葉を同時に取り除く亜種

次のような流儀もあり、全単射になる（M.C. Crabb. Counting nilpotent endomorphisms. Finite Fields and Their Applications, 12 (2006), 151-154.）。

• 以下の操作を \(k=1\) から始めて、\(k = n\) となるまで行う。
  1. \(T\) に \(l\) 個の葉 \(x_k, x_{k + 1}, \ldots, x_{k+l}\) （昇順）があるとする。各葉の親を \(y_k, y_{k+1}, \ldots, y_{k + l}\) とする。
  2. \(T \leftarrow T_k-x_k-x_{k+1}-\cdots-x_{k+l}, k \leftarrow k + l\)

頂点をベクトル、子から親への遷移を線形写像とみなすと、\(\mathbb{F}_q\) 係数冪零行列が \(q^{n(n-1)}\) 個あることが示せる。

問題演習

解答：\(m\) 個の葉が Prüfer コードに出現しないから \({n-1 \choose m}\sum_{i=0}^{n-1-m}{n-1-m \choose i}(-1)^i(n-m-i)^{n-2}\) 個。

解答：根 \(n\) が \(m-1\) 回 Prüfer コードに出現するから \({n-2 \choose m-1}(n-1)^{n-m-1}\) 個。

解答：森の各連結成分 \(G_i\) を縮約して 1 頂点にしたグラフを \(G’\) とする。\(G’\) の各頂点にはラベル \(1,2,…,n-m\) を付ける。Prüfer コード \(P(T)=(y_1,…,y_{n-m-2})\) は \(V(G’)^{n-m-2}\) への全単射で、次数 \(d(v)\) の頂点 \(v\) は \(y_1,…,y_{n-m-2}\) に \(d(v)-1\) 回出現する。また、縮約を解いた際、\(G’\) の頂点 \(i\) に接続する辺は、 \(G\) において \(|G_i|\) 通りの端点の接続方法がある。したがって \((\prod|G_i|)(\sum|G_i|)^{n-m-2}=n^{n-m-2}\prod|G_i|\) が答え。

\(kn^{n-k-1}\)通り。Pruferコードの構成で、頂点が \(1,2,\ldots,k\) のみになるまで頂点の除去を行うとき、最後に取り除かれた頂点の親が \(1,2,\ldots,k\) の \(k\) 通りあることに注意。

また、次のような示し方もある。\(p_k\) を \(k\) 個の連結成分からなる根付き森の個数とする。\(np_k=k{n \choose k} n^{n-k}\) を示せばよい。

• 左辺：根付き森の頂点 \(v\) を自由に選ぶ。\(v\) が含まれる連結成分の根を \(r\) とする。\(v\) を根とする部分木を切り離す。\(vP r^{\circ}\) パスをサイクル分解の標準形と思う。
• 右辺：出次数 \(0\) の \(k\) 個の頂点から一つを選び \(v\) とする。functional graph のサイクルをサイクル分解の標準形で並べてから、末尾に \(v\) を繋げる。

無向グラフ \(G\) のラプラシアンの固有多項式 \(f\) について、\(g(G, x) = f(-x)/(-x)\) と置くと
\(g(G, x) = (-1)^{n-1} \sum x^{l(F)-1} \) であることが、行列木定理から分かる。ただし、和は根付き森F全体を渡り、l(F)はFの連結成分の個数。代数的な計算により補グラフ\( \overline G\)のラプラシアンの固有値は、\(G\) の固有値 \(0, \lambda_1, \lambda_2, \ldots, \lambda_{n-1}\) に対して、\(0, n-\lambda_1, n-\lambda_2, \ldots, n-\lambda_{n-1}\) となることが分かる。従って、\(g(\overline G, x)=(-1)^{n-1}g(G, n-x)\) が成り立つ。これは、包除により導出できる。

\begin{align}
&(-1)^{n-1} g(G,n-x) \\
=& \sum (n-x)^{l(F)-1} \\
=& (-1)^{n-1} \sum {l(F)-1 \choose i-1}x^{i-1} n^{l(F)-i} (-1)^{n-i}
\end{align}
この式を、補グラフに含まれない辺集合E(F)に関する包除原理と見ます。Σの中身が、Fを部分グラフとして含む、i個の木からなる根付き木の個数×(±1)です。

Pruferコードで葉を順番に削除したとき、一番最後に削除する葉の親の選び方がn通り（親の連結成分に含まれるFの根を引き続き根として採用）、その他の根の選び方が \({l(F)-1 \choose i-1}\)通り（Fの根を再利用）、Pruferコードで削除する最後以外の葉の親の選び方が\(n^{l(F)-i-1}\)通りです。

従って、
\(g(\overline G, x)=(-1)^{n-1}g(G, n-x)\)
となります。

解答：問題１より、各頂点 \(i\) の次数が \(d_i\) であるラベル付き木の総数は \((\sum_{i=1}^n x_i)^{n-2}\) の \(\prod_{i=1}^n x_i^{d_i-1}\) の係数に等しい。従って、\(\left(\frac{d}{dx}x\right)^2(x+\sum_{i=2}^{n} 1)^{n-2}\) に \(x=1\) を代入してラベル付き木の総数 \(n^{n-2}\) で割った \((5-\frac{6}{n})(1-\frac{1}{n})\) が答え。

\(m=2\) のとき \(n_1^{n_2-1}n_2^{n_1-1}\)通り、\(m=n\) のとき \(n^{n-2}\) 通りであることは通常のPrüferコードから分かる。
解答：全域木 \(T\) のコード \(\mathcal{P’}(T)=(\sigma_1,\sigma_2,\ldots,\sigma_k,\sigma_\infty) \in W_1^{n_1-1} \times W_2^{n_2-1}\times \ldots \times W_k^{n_k-1} \times V^{m-2} \) を次のように構成する。

1. \((\sigma_1,\sigma_2,\ldots,\sigma_k,\sigma_\infty):=(\emptyset,\emptyset,\ldots,\emptyset,\emptyset)\)
2. \(T_1:=T\)
3. 以下の操作を \(k=1,2,\ldots,n-1\) について行う。
   1. \(T_k\) のラベル最小の葉を \(v\) 、その親を \(p\) 、\(v\) の属する部集合を \(V_a\) とする。
   2. \(T_k\) において \(V_a = \{v\}\) ならば \(\sigma_\infty\) の末尾、 さもなくば \(\sigma_a\) に \(p\) を追加する。
   3. \(T_{k+1}:=T_k-v\)

Prüfer コードと同様に削除済みの頂点と葉でない頂点に着目すれば次に削除される葉が分かり、全ての全域木 \(T\) と \(W_1^{n_1-1} \times W_2^{n_2-1}\times \ldots \times W_k^{n_k-1} \times V^{n-2}\) は全単射の関係にあることが示せる。従って、\(n^{m-2}\prod(n-n_i)^{n_i-1}\) が答え。

\(k=1\) のときは根付き全域木の数え上げになる。
解答：頂点 \(v\) とその隣接頂点の集合 \(N(v)\) が誘導する部分グラフが \(K^k\) と同型であるとき、頂点 \(v\) を k-leaf と呼ぶことにする。 Prüfer コードに倣って \(k\) 木 \(G\) に関する頂点の列 \(a\) と頂点集合の列 \(B\) を次のように作ろう。

1. \(G_1:=G\)
2. 以下の操作を \(i=1,2,\ldots,n-k\) について行う。
   1. \(G_i\) のラベル最小の k-leaf を \(a_i\), その隣接頂点の集合を \(B_i\) とする。
   2. \(G_{i+1}:=G_i-a_i\)

\(G\) に対して組 \((a, B)\) は単射である。この構成方法は、初期状態が \(K^k\) か \(K^{k+1}\) かという違いを無視すれば、 \(k\) 木の定義にある再帰的構築の逆再生である。定義に従って \(k\) 木を構築するとき、k-leaf になるのは (ii) で追加された頂点のみ、また k-leaf でなくなるのは、(ii) で追加された頂点の隣接頂点のみ。\(B_i \neq B_{n-k}\) とする。\(B_i\) のうち、最後に追加された頂点を \(p_i\) とする。\(p_i\) が \(d\) 番目に追加されたとすると、\(\# (B_{d} \cap B_i) = k-1 \) である。\(B_d\) のうち、\(B_i\) に含まれない唯一の頂点が、\(B_d\) の頂点のうち、\(q_i\) 番目に追加されたとする。2つの数 \((p_i, q_i) \in (V \setminus B_{n-k}) \times [k]\) から \(B_i\) を決定できる。全単射であることは、Prüfer コードと同様にすれば示せる。
以上から \(B_{n-k}\) を選ぶ \(n \choose k\) 通りも併せて \({n \choose k}(1+k(n-k))^{n-k-1}\) 通りが答え。

サイクル分解の標準形による導出

サイクル分解の標準形でも、完全多部グラフの全域木の個数が求まる（Omer, E. “A Bijection for Spanning Trees of Complete Multipartite Graphs.”）。
木の2頂点 \(a, b\) を自由に選び、\(a\) から \(b\) へのパスをサイクル分解の標準形とみなして、サイクルを作る。ただし、頂点のラベルは、組（属する部集合、部集合内での番号）に従って順序付ける。同じ部集合 \(W\) に属する２頂点 \(x, y\) が、サイクル分解の標準形において\((x..y)\) の形になるのは、\(W\) の頂点から始まる一番最後のサイクルだけである。また、一頂点のサイクル \((x)\) が現れるのも、一番最後だけである。一頂点のサイクルが高々一つしかないような functional graph は \(\prod ((n-n_i)^{n_i} + n_i(n-n_i)^{n_i-1}) = n^{m}\prod (n-n_i)^{n_i-1}\) 通りある。\(a, b\) の選び方が \(n^2\) 通りあるので、\(n^2\) で割ると答え。

参考文献

1. ヴァン・リント&ウィルソン 組合せ論 上
   • Prüfer コードの定義や全単射性の証明について参考にした。
2. Lewis, Richard P. “The number of spanning trees of a complete multipartite graph.” Discrete mathematics 197 (1999): 537-541.
   • 完全多部グラフの全域木の Prüfer コードについて参考にした。
3. Costa Pereira, P. R., Lilian Markenzon, and Oswaldo Vernet. “The Reduced Prufer Code for Rooted Labelled k-Trees.” ELECTRONIC NOTES IN DISCRETE MATHEMATICS 22.1 (2005): 135-139.
   • k 木の Prüfer コードについて参考にした。k 木にも Prüfer コードが応用できると知って驚いた。