正整数 \(n\) の素因数分解を deterministic に \(\tilde{O}(n^{1/4})\) で求める Strassen のアルゴリズムが面白かったので紹介します。

アルゴリズム

\(n\) bitサイズ（桁数）の整数同士の掛け算に必要なステップ数を \(\mathrm{M_{int}}(n)\) と置きます。\(\mathrm{M_{int}}(n)=O(n\log(n))\) のアルゴリズムがあるようなのですが、私は詳細を把握していないので語れないです、すみません。どの乗算アルゴリズムを使うかはほとんど関係ないので、\(\mathrm{M_{int}}\) で内部を覆い隠して議論を進めます。\(\mathrm{M_{int}}(n)=\tilde{O}(n)\) であれば、素因数分解を \(\tilde{O}(n^{1/4})\) ステップでするには十分です。

\(n\) の素因数のうち、\(n^{1/4}\) 以下のものは愚直に発見します。これは \(O(n^{1/4}\mathrm{M_{int}}(\log(n)))\) でできるので、\(n\) は \(n^{1/4}\) 超の素因数から成り立つと仮定して一般性を失いません。すると、\(n\) は高々３つの素数の積で書けます。また、\(n^{1/2}\) 超の素因数は高々１つしか存在しません。つまり \(\lceil n^{1/4} \rceil\) から \(\lfloor n^{1/2} \rfloor\) に含まれる素因数を１つ発見するアルゴリズムを構築すればよいです。

この段落ではアイディアを説明しますが、そのままでは破綻する部分があるので探しながら読んでみてください。Baby-step Giant-step を用います。\(M:=\lfloor n^{1/4} \rfloor\) に対して、$$f(x) := (x+1)(x+1)(x+2) \cdots (x+M)$$ と置きます。\(\lfloor n^{1/2} \rfloor\) 以下の正整数の積は$$n!=f(0)f(M)f(2M) \cdots f(M(M-1)) \prod_{i=M(M-1)+1}^{\lfloor n^{1/2} \rfloor} i!$$のように表せます。\(f(0),f(M),f(2M), \ldots ,f(M^2)\) を多点評価にて求めたとしましょう。各 \(i=0,1,\ldots,M\) に対して \(\gcd(n,f(iM))\) は \(n\) の素因数のうち \(iM+1,iM+2,\ldots,(i+1)M\) に共通するものからなります。\(\gcd(n,f(iM)) \neq 1\) ならばその区間に因数が含まれていると分かります。従って、\(i=0,1,2,\ldots,M\) について順に GCD を計算し、初めて \(\gcd(n,f(iM)) \neq 1\) となった区間 \((iM,(i+1)M]\) について愚直に素因数を探せばよいです。\(n\) の素因数は高々３個なので、高々２回このアルゴリズムを適用すれば \(n\) の素因数分解が終了します。

以上のアルゴリズムでは \(f(x)\) の係数が大きくなりすぎます。この問題は、\(\gcd(n,f(iM))\) は \(\bmod n\) を取っても変化しないことに着目して、\(\mathbb{Z}/n\mathbb{Z}\) 係数で \(f(x)\) を計算することにより解決します。\(\mathbb{Z}/n\mathbb{Z}\) 係数 \(d\) 次多項式 \(f,g\) の掛け算は、繰り上がりが起きないよう十分 base を大きくとった整数同士の掛け算とみなすことができます。つまり、\(n^2d\) 次進法で \(i\) 桁目がそれぞれ \([x^{i-1}]f,[x^{i-1}]g\) の整数の掛け算として計算してもよく、\(O(\mathrm{M_{int}}(d\log(n^2d))\) で求まります。従って \(f(x)\) は分割統治法により \(O(\mathrm{M_{int}}(n^{1/4}\log(n))\log(n))\) で計算できます。

ラグランジュ補間を用いた多点評価では mod g(x) が何度も登場しますが、\(\mathbb{Z}/n\mathbb{Z}\) には非可逆な元が存在するので mod g(x) が計算可能かは注意が必要です。mod g(x) は g(x) の最上位の項の係数が可逆ならば計算可能です。ラグランジュ補間を利用した多点評価は g(x) の最上位の係数が 1 の場合しか現れないので、mod g(x) を計算できます。従って、多点評価は可能です。

以上の計算量は GCD がボトルネックになって \(O(\mathrm{M_{int}}(n^{1/4}\log(n))\log(n)^2)\) です。\(\tilde{O}(n^{1/4})\) になっているのでここで終わってもよいのですが、\(\log(n)\) を一つ落とすのは簡単なのでやってしまいます。GCD は掛け算より \(O(\log n)\) だけ重いので、順に \(\gcd(n,f(iM))\) を計算せず、分割統治によって求めます。まず葉に \(f(iM)\) が、葉以外の頂点に子に書かれた数の積が書かれた２分木を構築します（下図）。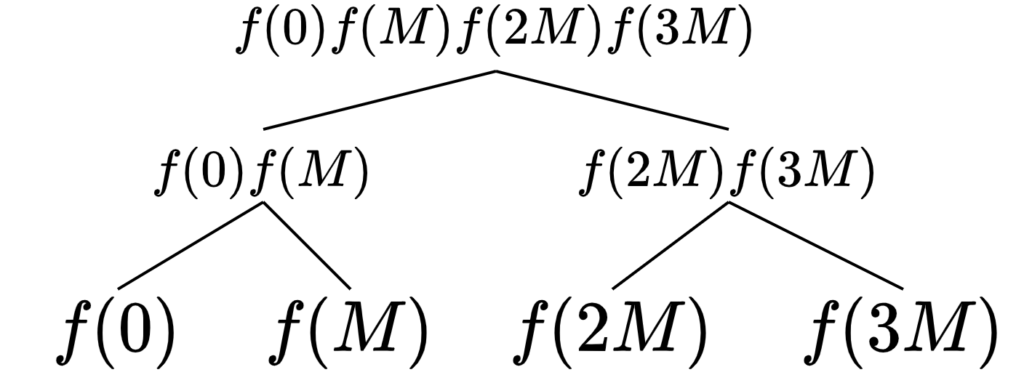

この根から、GCD が 1 にならない頂点を辿って葉に向かうと \(\gcd(f(iM),n) \neq 1\) なる \(i\) が（存在するなら）得られます（左子・右子両方 GCD≠1 なら左子に潜ります）。木の高さは \(O(\log(n))\) なので、全体で \(O(\mathrm{M_{int}}(n^{1/4}\log(n))\log(n))\) になります。

参考文献

1. Faster deterministic integer factorisation
   • wheel sieveと同じ要領で更に高速化しています。
2. Bostan, Alin, Pierrick Gaudry, and Éric Schost. “Linear recurrences with polynomial coefficients and application to integer factorization and Cartier–Manin operator.” SIAM Journal on Computing 36.6 (2007): 1777-1806.
   • \(f(x)\) と評価点の特殊な構造に基づいて、更に高速化しています。