Edmondsのアルゴリズムは、頂点数 \(N\)、辺数 \(M\) として、最小全域有向木を \(O(NM)\) で構築します。有向木とは下図のような、入次数高々１で閉路が存在しないグラフです。
各辺 \(c\) に重み \(c(e)\) が定まっているグラフ \(G\) の全域有向木であって、重みの和を最小化するものを、最小全域木と言います。
まず、Edmondsのアルゴリズムの準備として次の二つを示します。
下図のようなグラフです。
各頂点に入る辺で、重み最小のものを採用すれば良いです。
証明：\(n:=|E(C) \setminus E(B)| \geq 2\) と仮定して矛盾を導きます。有向閉路 \(C\) に沿って、\(B\) に採用されなかった辺を \((a_1,b_1),(a_2,b_2),\ldots,(a_n,b_n)\) とします。\(B\) で \(b_i\) に入る辺を \(f\) とします。\(f\) と \(e := (a_i, b_i) \) を交換しても、\(B\) の各頂点の入次数 1 のままです。\(c(e) < c(f)\) なので、\(e\) が採用されないためには、\(B-f+e\) に閉路ができなければなりません。つまり、\(B\) には \(b_i\)-\(a_i\) パスが存在します。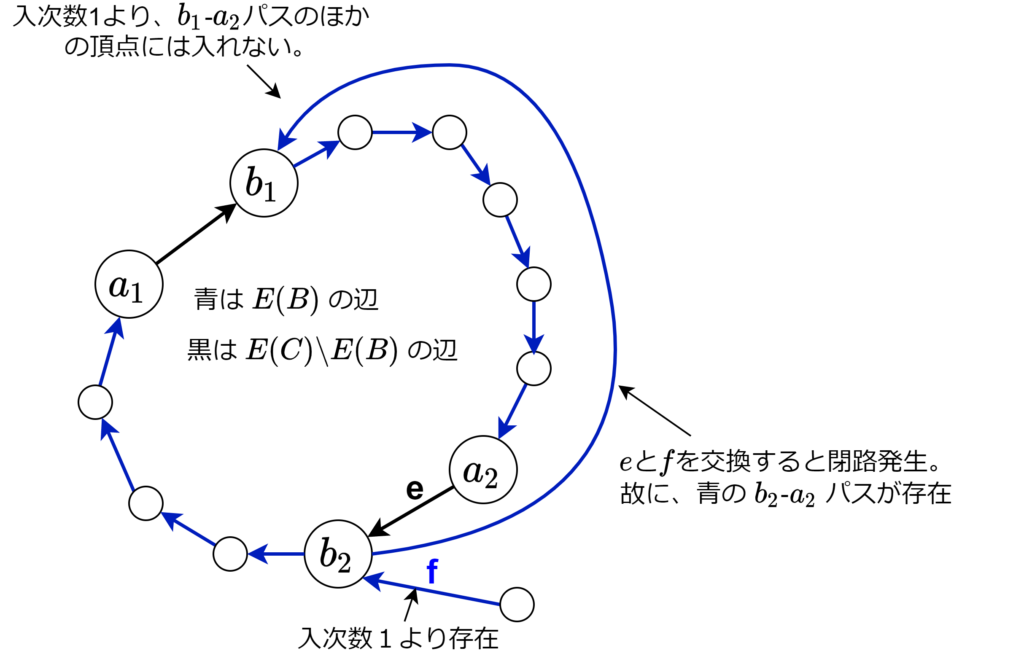
入次数1より \(b_i\)-\(a_i\) パスと \(b_{i-1}\)-\(a_i\)パスとの最初の交点 \(v\) は \(b_{i-1}\) になります。つまり、\(b_{i}\)-\(b_{i-1}\) パスが存在します（\(b_{0}:=b_n\)）。\(b_n\)-\(b_{n-1}\)パス、\(b_{n-1}\)-\(b_{n-2}\)パス、……、\(b_2\)-\(b_1\)パス、\(b_1\)-\(b_{n}\)パスをつなぐと、回路ができるので、\(B\) が有向木であることに矛盾。従って、\(n = 1\)。
Edmondsのアルゴリズム
Edmondsのアルゴリズムは \(O(NM)\) で最小有向全域木を構築します。最小有向なもり森の閉路は、一辺を除き、ある最小全域有向木 \(T\) に含まれました。最小全域有向木に含まれない閉路の辺を特定する必要があります。閉路 \(C\) に入る辺 \(e=(a, b)\) が採用されるなら、閉路の辺 \(f=(b, c) \in C(E)\) は、\(T\) の入次数１より不採用です。そこで、各閉路 \(C\) を縮約し、上記のような状況の全てのペア \((e, f)\) について \(c(e) \leftarrow c(e)-c(f)\) としたグラフを \(G’\) と置きます。\(G’\) の最小全域有向木 \(T’\) において、閉路の縮約を解き、\(T’\) が閉路に入る頂点で閉路を裂いたグラフは、\(G\) の最小有向全域木になっています。\(G’\) の辺数は \(G\) より１個以上少なくなるので、以上を繰り返すことで最小有向全域木が求まります。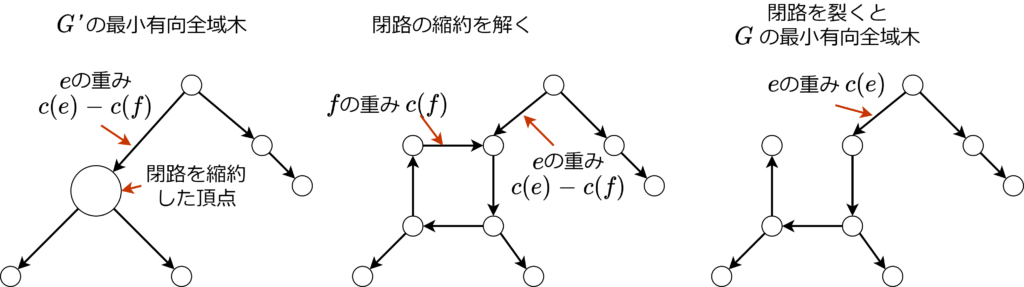
- 最小有向なもり森を求める。閉路が存在するなら２に移る。閉路が存在せず、最小有向全域木が求まっているなら３に飛ぶ。閉路が存在せず、最小全域有向木でもないならば、最小全域有向木が存在しない。
- 各閉路を1点に縮約する。その際、閉路の各辺 \(f=(b,c)\) について、\(b\) に入る辺 \(e\) の重みを \(c(e) \leftarrow c(e)-c(f)\) とする。１に戻る。
- １⇆２をバックトラックして、最小有向木に使われた辺を列挙する。
一回の１⇆２で辺が一つ以上減るから、１⇆２のループは \(N\) 回以下。最小なもり森は \(O(M)\) で求まるから、全体では \(O(NM)\) 。
フィボナッチヒープを使うと \(O(M+N\log(N))\) になるらしいです。
参考文献
組合せ最適化 by B. コルテ, J. フィーゲン
Comments