最小全域木を求めるアルゴリズムである、プリム法を解説します。

最小全域木とは、各辺 \(e\) に対して、重み \(w(e)\) が定まったグラフ \(G=(V,E)\) の全域木（頂点を全て含む木）のうち、重み最小のものです。

プリム法は最小全域木を \(O(m+n\log(n))\) で求めることができます。最小全域木を求めるアルゴリズムとしてほかにクラスカル法やブルーフカ法があります。

アルゴリズム

アルゴリズムは次の通りです。

1. 頂点 \(v\) を一つ選び、\(T\) を \(v\) のみからなるグラフとします。最終的に \(T\) が最小全域木になります。
2. 次の操作を、\(T\) が全域木となるまで繰り返します。
   1. \(V(T), V\setminus V(T)\) 間を結ぶ辺のうち、重み最小の辺 \(e\) を発見します。複数存在する場合はどれでもよいです。
   2. \(T \leftarrow T + e\) とします。

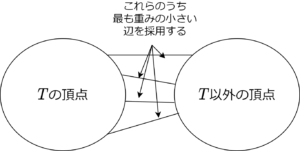\(V(T),V\setminus V(T)\) 間を結ぶ辺のうち重み最小の辺の発見 2-(i) は二分ヒープを用いると、\(O(\log(m))\) で発見できます（\(m\)：辺数）。(i)-(ii) は \(n-1\) 回繰り返すので、全体では \(O(m\log(n))\) です。

アルゴリズムの正当性

アルゴリズムの正当性を示します。

他のヒープで高速化

二分ヒープ以外のヒープを使って計算量を改善します。

\(m/n\)分ヒープ：\(m \log(n)/\log(m/n)\)

ヒープの内部の木を 2分木からx分木に変えると計算量がどうなるのか調べます。

キーの減算(decreaseKey）では、キーを減算したあと、そのキーを自分自身より子の方がキーが小さくなるまで、親とswapし続けます。swap回数は高さで抑えられるので、\(O(\log(n)/\log(x))\) 時間です。

最小キーの削除（deleteMin）では、根を木の末端のキーと交換して削除したあと、根のキーを自分自身より子の方が小さくなるまで、最小のキーの子とswapし続けます。swap回数は高さで抑えられ、各swapでは最小のキーの子を見つけるのに \(O(x)\) 掛かるので、全体で \(O(x\log(n)/\log(x))\) 時間です。

纏めると、木の高さが低くなる分だけdecreaseKeyが速くなり、子の数が増える分だけdeleteMinが遅くなります。プリム法ではdeleteMinが \(n-1\) 回、decreaseKeyが \(m\) 回行われるので、\(m \geq n-1\) より、deleteMinの速度を犠牲にキー追加の速度を向上させることができます。計算量は \(O((m+nx)\log(n)/\log(x))\) になるので、\(x=n/m\) のとき最適で \(O(m \log(n)/\log(m/n))\) になります。

特に \(m=n^{1+c}\) （\(c\) : 定数）のとき、\(O(m+n)\) となります。

子の数の最適化の例： 部分永続 Union Find, 最悪計算量最小化 Union Find

フィボナッチヒープ：\(O(m+n\log(n))\)

キーの値の減少（decrease-key）がならし \(O(1)\)、キーの追加が \(O(1)\)、最小値の取り出し（extract-min）が \(\log(q)\) (\(q\) : ヒープの要素数） でできるデータ構造として、フィボナッチヒープがあります。二分ヒープの代わりにフィボナッチヒープを使ってみます。

「\(V(T),V\setminus V(T)\) 間の辺で走査したもののうち、頂点 \(u \in V \setminus V(T)\) を端点に持ちコスト最小のもの」をフィボナッチヒープに挿入するキーにします。最小値を更新する辺 \(e=vu\) が見つかったときは decrease-key をすればよいです。縮約する辺を取り出す（extract-min）のに \(O(n\log(n))\) かかるので、全体の計算量は \(O(m+n\log(n))\) となります。これは、\(m/n\) 分ヒープを使った時より高速です。

おまけ

STARTを押すと、プリム法を可視化します（連打すると壊れます）。