multipoint evaluation (多点評価)とは、与えられた \(m\) 点での多項式の値を評価する問題です:
相異なる \(m\) 点 \(x_1, x_2, \ldots, x_m\) が与えられます。\(f(x) = \sum_{i=0}^n a_i x^i\) の各点での値 \(f(x_1), f(x_2), \ldots, f(x_m)\) を求めてください。
※ multipoint evaluation は多項式に対する操作であって、形式的べき級数に対する操作ではありません。
愚直に計算すると \(O(nm)\) ですが、工夫すると \(O(m \log(m)^2 + n\log(n))\) にできます。
アルゴリズム
アルゴリズムを構築します。カギになるのは剰余の定理です:
任意の \(a\) に対して \(f(a) = f(x) \bmod (x-a)\) が成立。
剰余の定理より、\(f(x) \bmod (x-x_1), f(x) \bmod (x-x_2), \ldots, f(x) \bmod (x-x_m)\) を列挙する問題に言い換えられます。\(k\) 次多項式の割り算には \(O(k \log (k))\) 時間が掛かるので、そのまま剰余の定理を適用すると \(O(nm \log(n))\) になってしまいます。そこで、doublingを使います。
まず、次の二つの条件を満たす根付き木 “subproduct tree” を構築します。
-
- \(m\) 個の葉があり、それぞれ \(x-x_1, x-x_2, \ldots, x-x_m\) が書いてあります。
- 葉以外の頂点には、子に書かれた多項式の積が書いてあります。
\(m = 4\) のときは下図のようになります。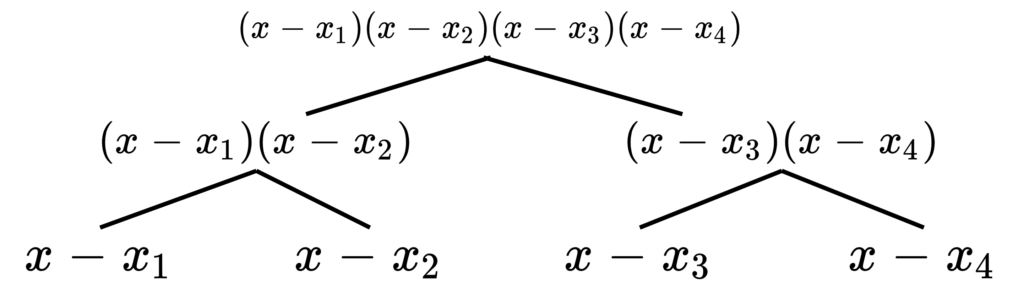 \(1\) が書かれた葉を全2分木になるまでつけ足しても答えは変わらず、\(m\) のオーダーも変化しません。従って、\(m=2^d\) だと仮定して一般性を失いません。subproduct tree の構築では \(2^k\)次多項式の掛け算が \(2^{d-k}\) 回現れます。掛け算の計算量が \(O(k2^k)\) なので全体では \(O(\sum_{k=0}^d 2^{d-k}k2^k) = O(2^dd^2) = O(m \log(m)^2)\) です。
\(1\) が書かれた葉を全2分木になるまでつけ足しても答えは変わらず、\(m\) のオーダーも変化しません。従って、\(m=2^d\) だと仮定して一般性を失いません。subproduct tree の構築では \(2^k\)次多項式の掛け算が \(2^{d-k}\) 回現れます。掛け算の計算量が \(O(k2^k)\) なので全体では \(O(\sum_{k=0}^d 2^{d-k}k2^k) = O(2^dd^2) = O(m \log(m)^2)\) です。
次に、subproduct tree に書かれた多項式で \(f(x)\) を割った余りを、各頂点に書いた根付き木 “subremainder tree”を構築します。subremainder tree の葉に書き込まれた余りが、求めたい値です。親に書き込まれた多項式が \(f \bmod g_0g_1\)、自身に書き込まれた多項式が \(f \bmod g_0\) だとすると、\((f \bmod g_0g_1) \bmod g_0 = f \bmod g_0 \) が成り立ちます。この式に従って根から順に BFS で余りを書き込んでいきます。
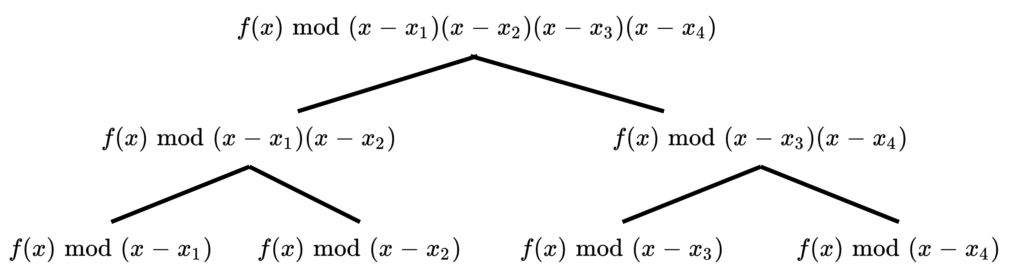
subremainder tree の計算量は subproduct tree と同様に計算すると \(O(m\log(m)^2 + n\log(n))\) となります(2項目は根の余りを計算する計算量)。全体の計算量も \(O(m\log(m)^2+n\log(n))\) となります。
評価点が等比数列のとき(Chirp Z-transform)
評価する点が等比数列 \(x_1=q^1,x_2=q^2,\ldots,x_m=q^m\) のとき、\(O(n\log(n))\) で multipoint evaluation できます。FFTの一般化です。
\(2ij = (i+j)^2-i^2-j^2\) を用いて、
\begin{align} f(q^j) =& \sum_{i=0}^{n-1} a_iq^{ij} \\
=& q^{-j^2/2} \sum_{i=0}^{n-1} a_iq^{-i^2/2} \cdot q^{(i+j)^2/2}\end{align}となります。\(\sum\) の中が畳み込みの形なので、FFTで \(O((n+m)\log(n+m))\) です。\(q^{1/2}\) が \(f(x)\) の係数体に含まれないときは、添加して拡大する必要があることに注意。$$ij = {i+j \choose 2}-{i \choose 2}-{j \choose 2} $$ を使えば、全て偶数になって、\(q^{1/2}\) が出てこないようにすることができる(熨斗袋さんの解説)。
multipoint evaluationの転置
余談ですが、\(f(x) := \sum_{i=0}^n a_i x^i \) を \(x_0, \ldots, x_m\) で求めよという問題は、
$$\begin{pmatrix}f(x_{0}) \\ f(x_{1}) \\ \vdots \\ f(x_m) \end{pmatrix}=\begin{pmatrix}x_{0}^0 & x_{0}^1 & \ldots & x_{0}^n \\ x_{1}^0 & x_{1}^1 & \ldots & x_{1}^n \\ \vdots & \vdots & \ddots & \vdots \\ x_{m}^0 & x_{m}^1 & \ldots & x_{m}^n \end{pmatrix}\begin{pmatrix}a_{0} \\ a_{1} \\ \vdots \\ a_n \end{pmatrix}$$という行列とベクトルの積を求める問題に言い換えられます。Tellegen’s principle より、転置を取った$$\begin{pmatrix}v_{0} \\ v_{1} \\ \vdots \\ v_n \end{pmatrix}=\begin{pmatrix}x_{0}^0 & x_{1}^0 & \ldots & x_{m}^0 \\ x_{0}^1 & x_{1}^1 & \ldots & x_{m}^1 \\ \vdots & \vdots & \ddots & \vdots \\ x_{0}^n & x_{1}^n & \ldots & x_{m}^n \end{pmatrix}\begin{pmatrix}b_{0} \\ b_{1} \\ \vdots \\ b_m \end{pmatrix}$$を(入出力を除き)同じ計算量で求めるアルゴリズムを機械的に導出できます。逆にこちらの問題は \(\sum_{i=1}^n v_it^i = \sum_{i=1}^n \frac{b_i}{1-x_it} \bmod t^{n+1}\) を求めよという問題に言い換えられ、分割統治で通分していくことで multipoint evaluation と同じ計算量 \(O(m\log(m)^2+n\log(n))\) になります。そして、Tellegen’s principle により multipoint evaluation のアルゴリズムが機械的に導出できます。
演習問題
解答:\(M:=\lfloor \sqrt{N} \rfloor\) と置きます。まず、\(f(x):=\prod_{i=1}^{M}(i+x)\) を分割統治法を用いて \(O(M\log(M)^2)\) で求めます。\(f(x)\) と \(N!\) の間に $$N!=f(0)f(M)f(2M) \cdots f(M(M-1)) \prod_{i=M^2+1}^N i$$ が成り立ちます。\(f(0),f(M),f(2M),\ldots,f(M(M-1))\) は multipoint evaluation により \(O(M\log(p)^2)\) で求まります。\(O(N-M^2)=O(M)\) なので、全体で所望の計算量を達成できました。
更に工夫すると、\(O(\log p)\) を落とせることが知られています[4]。
解答:こちらで熨斗袋さんに教えて頂きました。1変数ずつFFTします。通常、FFT では各 \(n_i\) を \(2\) 冪にキャストするため、\(O(2^K)\) だけ余分に掛かってしまいます。評価点が等比数列なら個数 \(n\) が2冪でなくとも多項式補間・評価が \(O(n\log(n))\) でできることを用いると、この \(O(2^K)\) は消すことができます。計算量解析はmaspyさんに教えて頂きました。
解答:こちらでSSRSさんに教えて頂きました。\(g(S) = 「\) \(U\) を集合の列 \((U_1, U_2, \ldots, U_k)\) に分割する方法のうち、\(i \not \in S\) について、\(U_i = \emptyset\) となる場合の数」とすると、求める値は包除原理より
\begin{align}
&\frac{1}{k!}\sum_{T \subset [k]}g(T)(-1)^{|S|-|T|} \\
=&\frac{1}{k!}\sum_{i} {k \choose i}(-1)^{k-i}\prod_j \left(\!\!\!{i \choose a_j}\!\!\!\right)
\end{align}
となります。\(\prod_j \left(\!\!\!{x \choose a_j}\!\!\!\right)\) は一次式の積の形をした \(n\) 次多項式なので、\(O(n \log(n)^2)\) で求められます。また、\(x = 0, 1, \ldots, n\) での多点評価も \(O(n \log(n)^2)\) でできます。
参考文献
- Borodin, Allan, and Robert Moenck. “Fast modular transforms.” Journal of Computer and System Sciences 8.3 (1974): 366-386.
- このアルゴリズムが提案された論文
- Bostan, Alin, Grégoire Lecerf, and Éric Schost. “Tellegen’s principle into practice.” Proceedings of the 2003 international symposium on Symbolic and algebraic computation. 2003.
- Tellegens’s principle を用いて multipoint evaluation を定数倍高速化しています。
- アルゴリズム/データ構造を語る会第1回tkoさん
- Alin Bostan, Pierrick Gaudry, and Eric Schost, Linear recurrences with polynomial coefficients and application to integer factorization and Cartier-Manin operator.
初めまして。
37zigen さんのアルゴリズム/データ構造の記事をいつも楽しく拝読させて頂いている者です。
つまらない誤植の指摘ですが、multipoint evaluation の記事について、
> 剰余の定理より、f(x)mod(x−x_1),f(x)mod(x−x_2),…,f(x)mod(x−x_n)を列挙する問題に言い換えられます。
とありますが、正しくは f(x)mod(x−x_1),f(x)mod(x−x_2),…,f(x)mod(x−x_m) でしょうか?
その通りでした。ご指摘ありがとうございます。