この記事では部分永続配列(fat nodes)と全永続配列(永続 m 分木を流用)を解説する。永続配列が使えるようになると、配列を用いて実装されるデータ構造(Union Find、セグメント木など)は、その配列を永続配列に置き換えるだけで機械的に永続化できるようになる。多くのデータ構造が、最適な計算量ではないにしても、永続化できるようになるだろう。
部分永続配列
部分永続配列とは、次のような問題を処理するデータ構造である:
- \(a_{i-1}[p_i]\) を \(v_i\) で更新した配列を \(a_i\) とする。
- \(a_{t_i}[p_i]\) を出力せよ。ただし \(0 \leq t_i < i\) とする。
ここでは fat nodes と呼ばれる、更新履歴を配列 a の各インデックスに積む方法を紹介する。配列 a の各インデックス i について、a[i] の (更新時刻, 更新後の値) のペアを、時系列順に並べて配列 \(b_i\) として管理する。すると、\(a_t[i]\) は、\(b_i\) のペアのうち、更新時刻が t 以下最大のものの更新後の値に等しい(Predecessor Problem)。二分探索すると、Q を更新回数として \(O(\log Q)\) でペアが得られる。
部分永続配列はクエリ当りならし \(O(\log Q)\) で実現できることが分かった。ならしは配列 \(b_i\) を動的にする部分で生じている。コード(C++)は次のようになる:
#include "vector"
using namespace std;
struct PartialPersistentArray {
vector<vector<pair<int, int>>> b;
int last_time = 0;
// 時刻 -1 における a を設定する。
PartialPersistentArray(vector a) {
b.resize(a.size());
for (int i=0; i < a.size(); ++i) {
b[i].push_back(make_pair(-1, a[i]));
}
}
// 時刻 last_time において、a[i] <- val と更新する。
void set(int i, int val) {
b[i].push_back(make_pair(last_time++, val));
}
// 時刻 time における a[i] の値を返す。
int get(int i, int time) {
int ok = 0, ng = b[i].size();
while (ng - ok > 1) {
int middle = (ok + ng) / 2;
if (b[i][middle].first <= time) {
ok = middle;
} else {
ng = middle;
}
}
return b[i][ok].second;
}
};この fat node のアイディアは素朴ではあるが、クエリ当り \(O(\log(n)/\log(\log(n)))\) の全永続配列[2]や、クエリ当り \(O(\log(\log(n)))\) の部分永続 Union Find (解説:koprickyさん、熨斗袋さん)に応用できる。
全永続配列
全永続配列とは、次のような問題を処理するデータ構造である:
- 配列 \(a_{t_i}[p_i]\) を \(v_i\) で更新した配列を \(a_i\) とする。
- \(a_{t_i}[p_i]\) を出力せよ。
ただし \(0 \leq t_i < i\) とする。
次に、全永続完全 m 分木を流用して、全永続配列を実現する方法を解説する。
全永続完全 m 分木による全永続配列
path copying と呼ばれる方法で、有向完全 m 分木を全永続化する(子へのポインタを持つ)。全永続化に当たって、元々ある頂点・辺を破壊してはいけない。そこで、まず更新したい頂点(赤色)と根を結ぶパスを複製する。そして、その複製したパス(青)に接続する部分木を、元々のパスと共有するように有向辺を張ればよい(下図)。各更新時刻に対して、更新後の木の根 r を持つ。すると、特定の時刻の頂点へのアクセスは根 r からの探索によって実現できる。
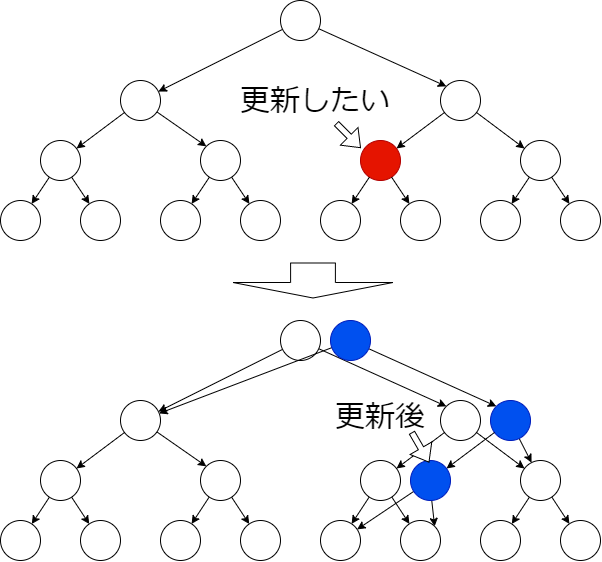
頂点数 n の m 分木の高さが \(O(\log_m n)\) であるから、更新 \(O(m \log_m n)\) 、読み取り \(O(\log_m n)\) である。
部分永続 Union Find
子の数 m は更新と読み取りの比率に応じて最適値にするとよい。例えば、link by size(経路圧縮なし)の Union Find を永続配列を用いて永続化したいとする。このとき、書き込み 1 回当り \(O(\log n)\) 回読み取りが生じうる。\(O(1 \times m \log_m n + \log n \times \log_m n)\) を最小化したい。\(m=\log n\) のとき最小になり、1クエリ当り \(O(\log(n)^2 / \log \log n)\) となる。
同じアイディアの適用例:多分ヒープによるプリム法、最悪計算量最小化 Union Find
アドホックに設計すると、実時間 \(O(\log(n))\) にできる(熨斗袋さんの解説)。同じことをk-ufですると最悪計算量はそのまま、ならし \(O(\log(n)/\log\log(n))\) にできる。
データの持ち方
永続化する配列 a の木への載せ方は色々な流儀がある。下の画像の、1つ目は最上位の桁から順に場合分けする方法、2つ目は最下位の桁から順に場合分けする方法、3つ目は2つ目の方法を発展させた内部ノードを無駄にしない方法である。2つ目、3つ目は1つ目に比べて実装が少し軽くなる。ただし、区間クエリを扱いたい場合は1つ目を使うのがよい(永続セグメント木に拡張する場合)。
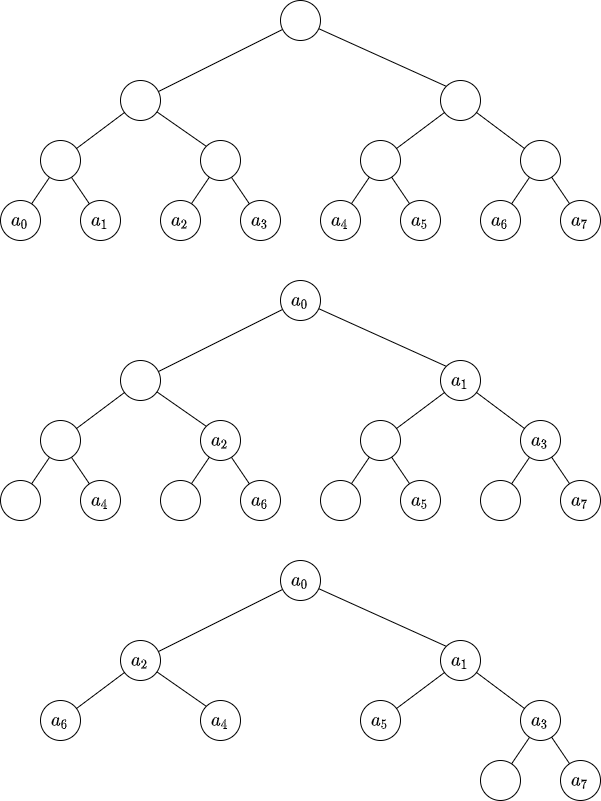
2つ目の方法で a[id] に access するコード(Java)は次のようになる(m 分木):
int access(int id) {
return id == 0 ? val : child[id % m].access(id / m);
}3つ目の方法にするには id / m を (id – 1) / m とすればよい。永続 m 分木を流用した永続配列のコード(Java)は次のようになる。2つめの流儀で実装した:
class PersistentArray {
final int m = 32;
PersistentArray[] ch = new PersistentArray[m];
int val;
public PersistentArray() {
}
PersistentArray build(int[] a) {
PersistentArray root = new PersistentArray();
for (int i = 0; i < a.length; ++i)
root = dfs(root, i, a[i]);
return root;
}
PersistentArray dfs(PersistentArray cur, int i, int val) {
if (cur == null)
cur = new PersistentArray();
if (i == 0) {
cur.val = val;
} else {
cur.ch[i % m] = dfs(cur.ch[i % m], i / m, val);
}
return cur;
}
PersistentArray set(int i, int new_val) {
PersistentArray ret = new PersistentArray();
ret.val = val;
for (int j = 0; j < m; ++j)
ret.ch[j] = ch[j];
if (i == 0) {
ret.val = new_val;
return ret;
}
ret.ch[i % m] = ch[i % m].set(i / m, new_val);
return ret;
}
PersistentArray add(int i, int add) {
return set(i, get(i) + add);
}
int get(int i) {
return i == 0 ? val : ch[i % m].get(i / m);
}
}参考文献
- CombNaf3 -Final- : 木構造の永続化(熨斗袋さん)
- Dietz, Paul F. “Fully persistent arrays.” Workshop on Algorithms and Data Structures. Springer, Berlin, Heidelberg, 1989.
- 熨斗袋さんのTweet
Comments