\(r\) 頂点完全グラフ \(K^r\) を含まない辺の数が最大のグラフとは何か。この疑問に答える Turán の定理を解説する。もしそのようなグラフの部集合の数が \(r-1\) 個以下ならば、いくら辺を増やしても \(K^r\) を含み得ないから、完全多部グラフである。また、部集合の数が多い方が辺の数が多いから \(r-1\) 部グラフである。直感的には部集合のサイズが揃っている方が辺数は多そうである。実際、サイズ \(A, A+d\) の2つの部集合のサイズを \(A+1, A+d-1\) にすれば辺の数は \(d-1\) だけ増える。つまり、部集合のサイズは互いに高々一つしか異ならない。このような \(n\) 頂点 \(r-1\) 部完全グラフを Turán グラフ \(T^{r-1}(n)\) といい、辺の数を \(t_{r-1} (n)\) で表す。例えば \(T^2(7)、T^3(8)\) は下図のようになる。
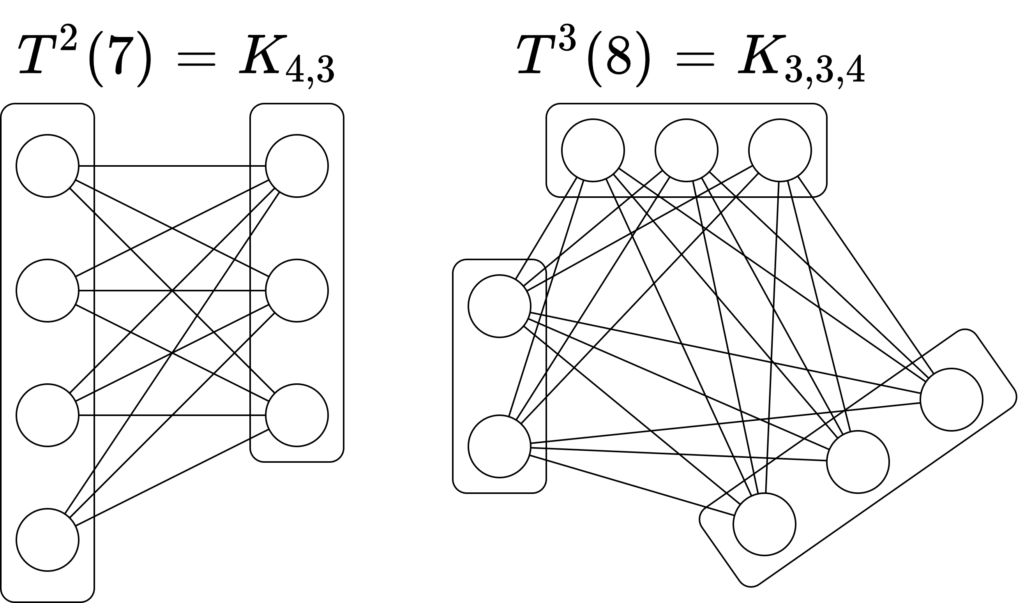
\(r\) と \(n\) が決まると、Turán グラフは一意に定まる事に注意。Turán の定理はこの Turán グラフが \(K^r\) を含まない辺数最大のグラフであることを表している。
頂点数 \(n\) のグラフのうち、\(r\) 頂点完全グラフ \(K^r\) を部分グラフに含まない辺数最大のグラフ \(G\) は Turán グラフ \(T^{r-1}(n)\) 唯一である。
以下ではこの定理の証明を幾つか見ていく。
1. Zykov’s Symmetrisation による証明
頂点 \(v\) と同じ隣接頂点を持つ頂点 \(v’\) を追加する操作を頂点 \(v\) の複製と呼ぶことにする。この操作の前後では、\(K^r\) を含まないという性質は保たれ、上手く利用することで次のようにより辺数の多い \(K^r\) を含まないグラフが構成できる。このテクニックを Zykov’s Symmetrisation という。
G が完全多部グラフであることを示す。完全多部グラフでないと仮定する。
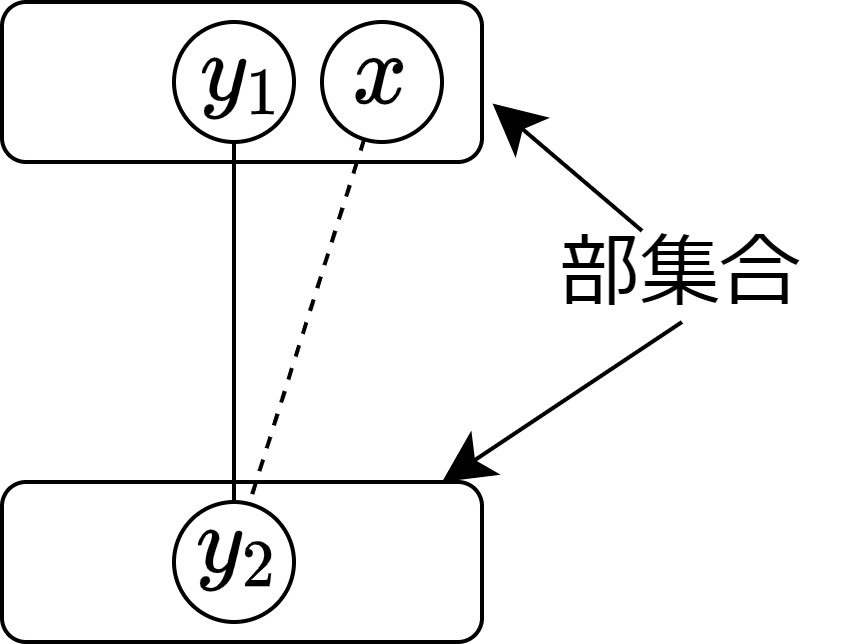 各頂点を一つの部集合に割り当てれば、n 頂点のグラフは n 部集合に分けられる。隣接していない部集合を合体しても部集合のままであるから、隣接していない部集合がなくなるまで合体を繰り返す。完全多部グラフでないから、図のように、\(xy_1, xy_2 \notin E(G), y_1y_2 \in E(G)\) となる頂点 \(x,y_1,y_2\) が取れる。
各頂点を一つの部集合に割り当てれば、n 頂点のグラフは n 部集合に分けられる。隣接していない部集合を合体しても部集合のままであるから、隣接していない部集合がなくなるまで合体を繰り返す。完全多部グラフでないから、図のように、\(xy_1, xy_2 \notin E(G), y_1y_2 \in E(G)\) となる頂点 \(x,y_1,y_2\) が取れる。
(i) 次数 \( d(x) < d(y_1) \) のとき
頂点 \(x\) を消去して頂点 \(y_1\) を複製する。
(ii) 次数 \( d(x) < d(y_2) \) のとき
頂点 \(x\) を消去して頂点 \(y_2\) を複製する。
(iii) 次数 \( d(x) \geq d(y_1) \) かつ \( d(x) \geq d(y_2) \) のとき
頂点 \(y_1,y_2\) を消去して頂点 \(x\) を 2 回複製する。
いずれの場合も頂点数を不変のまま、\(K^r\) を含まないより辺数の多いグラフを構成できたので矛盾。従って G は完全多部グラフである。完全多部グラフのうち、辺数が最も多くなるのは Turán グラフのときであったから証明完了。
2. Turán グラフの再帰的構造による証明
・再帰的構造による証明1(by Turán)
\(T^{r-1}(n)\) の部集合からそれぞれ一つずつ頂点を削除すると下図のように \(T^{r-1}(n-(r-1)) \) が得られる。また、削除した頂点は元のグラフで完全グラフ \(K^{r-1}\) をなす。この再帰的構造を用いたのが次の証明である。
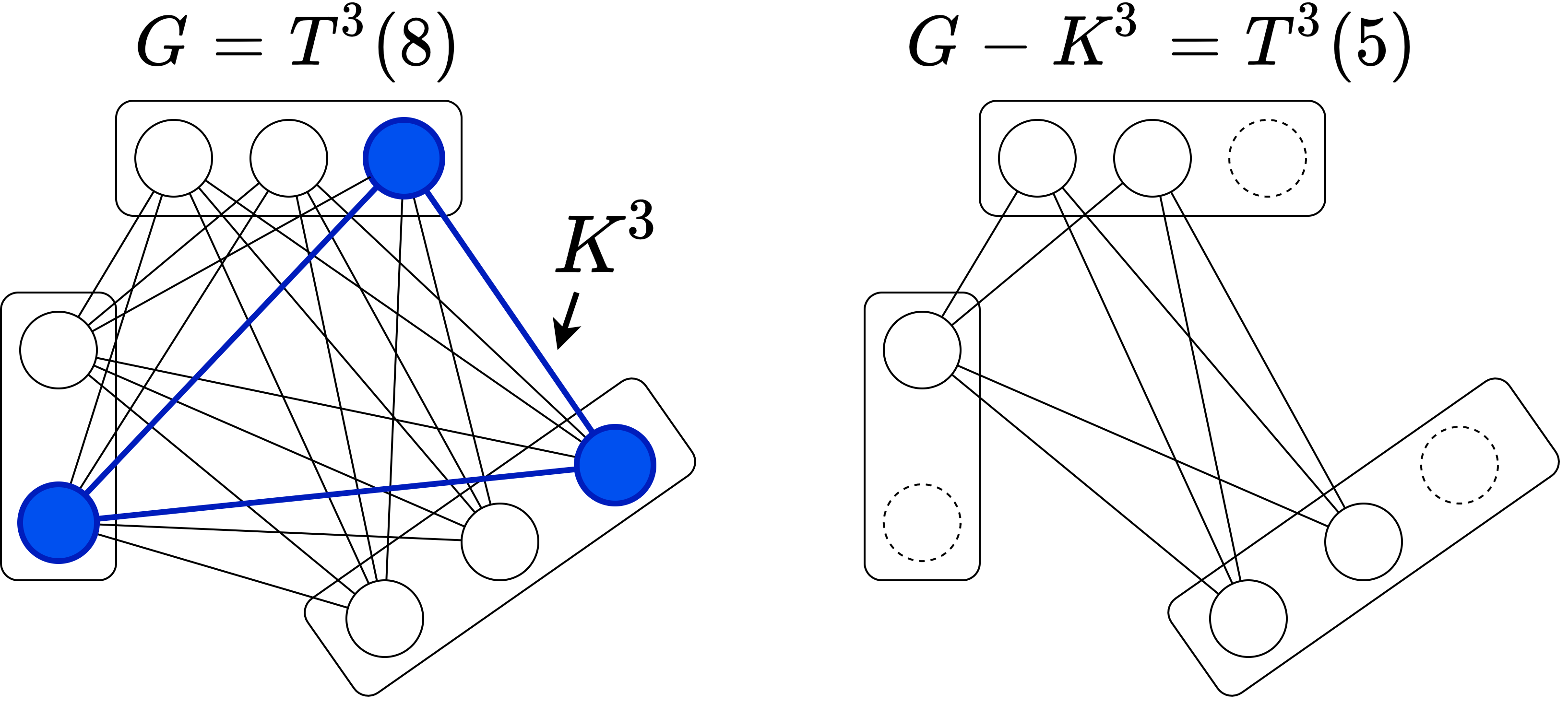
頂点数に関する帰納法で \(G\) が Turán グラフであることを示す。頂点数 \(n (< r)\) のとき \(G=K^n\) だから Turán の定理は成立。頂点数 \(n(\geq r)\) 未満のとき Turán の定理が成立することを仮定する。
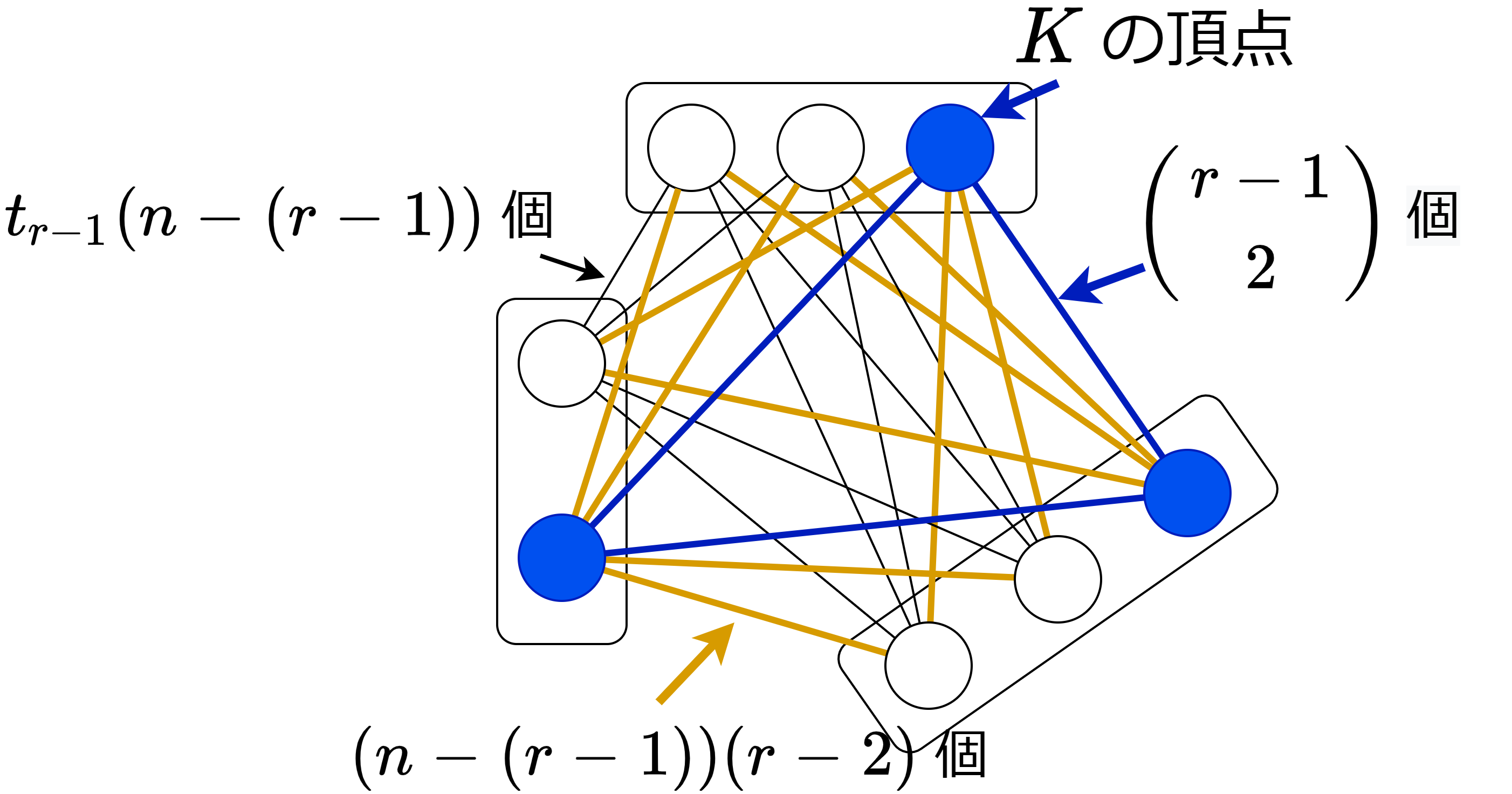
辺数の最大性より、\(G\) に 1 辺 \(e\) を追加した \(G+e\) は \(K^r\) を部分グラフに含む。よって \(G\) は \(K^{r-1}\) を部分グラフに持つ。部分グラフ \(K^{r-1}\) を 1 つ固定して \(K\) と置く。\(K\) の頂点を削除したグラフ \(G-K\) は \(K^{r}\) を部分グラフに持たないから、辺数は \(t_{r-1}(n-(r-1))\) で抑えられる。\(H\) の各頂点 \(v\) は \(K\) の高々 \(r-2\) 個の頂点としか隣接しない。さもなくば \(K * v \cong K^r\) が \(G\) の部分グラフとなり矛盾。以上から、次の不等式で \(G\) の辺数 \(||G||\) が抑えられる:
$$||G|| \leq t_{r-1}\left(n-(r-1)\right)+(n-(r-1))(r-2)+{r-1\choose 2}.$$下図から不等式の右辺は \(t_{r-1}(n)\) と等しい。\(||G||\) の辺数の最大性から不等号は等号で常に成立。よって \(G-K\) は Turán グラフ \(T^{r-1}(n-(r-1))\) である。\(K\) の各頂点 \(v\) を \(G-K=T^{r-1}(n-(r-1))\) の非隣接な頂点の部集合に追加すれば、\(G\) は Turán グラフ \(T^{r-1}(n)\) となる。
・再帰的構造による証明2
Turán グラフ \(T^{r-1}(n)\) の次数最小の頂点 \(v\) を削除すると、下図のように \(T^{r-1}(n)-v=T^{r-1}(n-1)\) が得られる。この再帰的構造を用いたのが次の証明である。
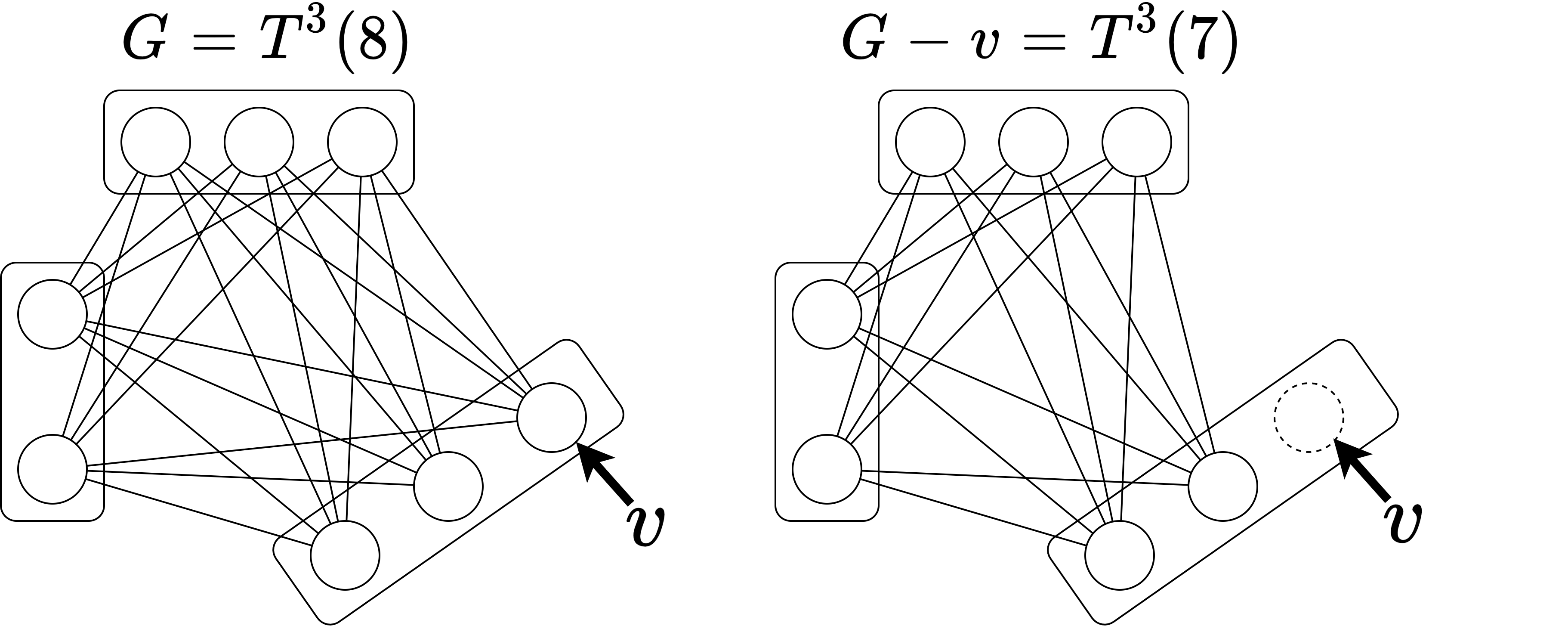
Turán グラフは \(K^r\) を含まないことについて辺極大である。従って、\(K^r\) を含まない辺数 \(t_{r-1}(n)\) のグラフが Turán グラフのみであることを示せばよい。なぜなら、辺数 \(t_{r-1}(n)+1\) 以上の \(K^r\) を含まないグラフが存在するならば、辺極大であるはずの Turán グラフを部分グラフに持ち矛盾するからである。
頂点数についての帰納法で示す。1頂点のときは成立。
\(|G|\) 頂点未満のとき成立を仮定する。
次数最小の頂点 \(v\) について \(G-v\) の辺数は \(t_{r}(n-1)\) 以上。\(G-v\) は \(K^r\) を含まないから帰納法の仮定より \(G-v=T^{r}(n-1)\) である。\(v\) が \(T^{r}(n-1)\) の全ての部集合の頂点と隣接すると \(K^r\) が生じてしまうから、\(G=T^{r}(n)\) となる。\(|G|\) 頂点のときも成立したので証明完了。
・再帰的構造による証明3
詳細は述べないが、部集合の個数を一つ減少して、\(T^{r-1}(n)\) から \(T^{r-2}(n)\) を生成するような再帰的構造を用いた証明もある。詳細は Andrzej Czygrinow 氏の授業ノートを参照せよ。
弱い主張と証明
Turán グラフ \(T^{r-1}(n)\) がサイズ \(t\) の部集合 \(a\) 個とサイズ \(t + 1\) の部集合 \(r-1-a\) 個からなるとすると
$$T^{r-1}(n)=\frac{n^2}{2}\frac{r-2}{r-1}-\frac{a((r-1)-a)}{2(r-1)}
\leq \frac{n^2}{2}\frac{r-2}{r-1} $$
となる。不等号は部集合のサイズが揃っているときに成り立つ。次の2つの証明では弱い主張「 \(K^r\) を含まないグラフの辺数が不等号の右辺 \(\frac{n^2}{2}\frac{r-2}{r-1}\) 以下であること」を示す。
1. 謎の証明方法
この証明方法は謎である。面白いが、何をしているのかよく分からない。
各頂点 \(i\) に \(\sum w_i = 1\) を満たすように非負の重み \(w_i\) を割り振る。\(S:=\sum_{(i,j)\in E(G)} w_iw_j\) を最大化してみよう。
非隣接な2頂点 \(u,v\) の隣接頂点の重みの総和が \(x,y\ (x \geq y)\) だとする。微小量 \(\varepsilon > 0\) に対して、$$x(w_u+\varepsilon)+y(w_v-\varepsilon) \geq xw_u+yw_v$$だから、\(S\) を減少させずに特定のクリークに重みを集めることができる。
頂点 \(1,2,\ldots,m\) からなるクリーク \(K^m\) に重みを集めると \(2S\) は次のようになる:\begin{align}
2\sum_{(i,j)\in E(K^m)} z_iz_j
=&\left(\sum_{i=1}^m z_i\right)^2-\sum_{i=1}^m z_i^2\\
=&1-\sum_{i=1}^m z_i^2\\
\leq&1-\frac{1}{m}\sum_{i=1}^m z_i\\
=&1-\frac{1}{m}
\end{align}2行目から3行目にかけてコーシー・シュワルツの不等式を用いた。等号は \(z_i=1/m\) のとき成立。 \(m\) が大きいほどその値は大きくなる。\(G\) は \(K^r\) を部分グラフに持たないことについて辺極大だから、\(K^{r-1}\) を部分グラフに持つ。全ての重みが \(z_{i}=1/n\) のとき \(S=\frac{||G||}{n^2} \frac{1}{2}\leq (1-\frac{1}{r-1})\) であるから $$||G||\leq \frac{n^2}{2}\frac{r-2}{r-1}$$を得る。
2. 次数を用いたクリークの発見による証明
次数の大きさからある大きさのクリークの存在が必ず言えることを用いた証明。
クリークをなす頂点集合 \(U\) のサイズを求めたい。
\(\{1,2,\ldots,n\}\) のランダムな置換 \(\{\pi(1),\pi(2),\ldots,\pi(n)\}\) の先頭から順に頂点 \(v=\pi(i)\) を選ぶ。最初 \(U\) は空集合である。頂点 \(v\) を \(U\) に加えてもクリークならば、\(U\) に \(v\) を加える。\(v\) が \(U\) に加えられる確率は \(v\) が、 \(v\) の隣接頂点以外の頂点 \(n-d(v)-1\) 個より先に選ばれる確率 \(\frac{1}{n-d(v)}\) と等しい。よって \(|U|\) の期待値は \(\sum_{v \in V(G)} \frac{1}{n-d(v)}\) であるから \(G\) は必ずサイズ \(\lceil\sum_{v\in V(G)} \frac{1}{n-d(v)}\rceil\) 以上のクリークを部分グラフに持つ。
\(|G|\) が \(K^r\) を部分グラフに持たないという条件から次を得る:\begin{align}
r-1 \geq &\sum_{v \in V(G)} \frac{1}{n-d(v)}\\
\geq &\frac{n}{n-\sum_{v \in V(G)} \frac{d(v)}{n}}\\
=&\frac{n}{n-\frac{2||G||}{n}}
\end{align}2行目から3行目にかけてイェンセンの不等式を用いた。\(G\) について解いて \(||G||\leq \frac{n^2}{2}\frac{r-2}{r-1}\) を得る。
参考文献
- Diestel, Reinhard. “Graph theory. 1997.” Grad. Texts in Math 2 (2016). Section 7.1. (preview)
- 簡潔にまとまっています。
- ヴァン・リント&ウィルソン 組合せ論 上 第 4 章
- 謎の証明方法をこの本で読んで、とても印象に残りました。
- Andrzej Czygrinow 氏の授業ノート
- この記事では扱わなかった再帰的構造を用いた証明が載っています。
- “Extremal Graph Theory”. B. Bollobas.
Comments