Union Find の計算量

Union Find の計算量を解説する。

1 二項木とは
2 Union by Size の計算量
3 Union by Rank の計算量
4 経路圧縮の計算量解析
- 4.1 分割統治による証明
- 4.2 ポテンシャルを使った証明
5 Path Compression の最悪ケース
6 Union by Rank, Size と経路圧縮の組み合わせ
7 そして$\alpha(n)$へ………
8 findを繰り返したときの計算量
9 参考文献
10 関連記事

二項木とは

いくつかの種類の Union Find において最悪ケースを与える二項木 $B_k$ を最初に紹介する。
二項木を

$B_0$ は 1 頂点からなる根付き木
$B_{k+1}$ は、根の子をそれぞれ新たな根とする部分木が $B_0,B_1,\ldots,B_{k}$ である根付き木

と定義する。$B_0,B_1,B_2,B_3,B_4$を図示すると下図のようになる。

帰納法から二項木 $B_k$ は頂点数 $2^k$ 、高さ $k$ である。
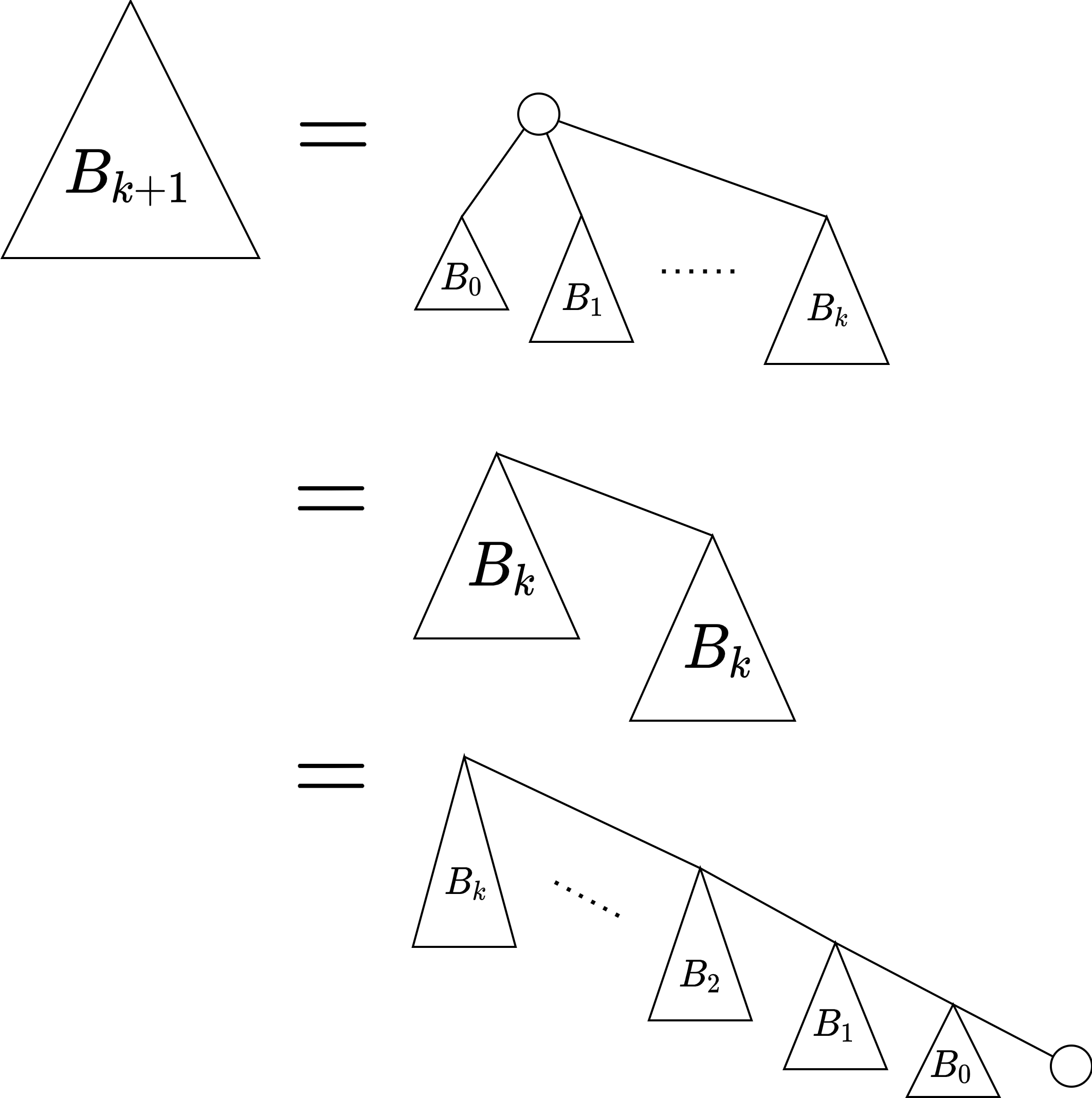
二項木の構成方法
帰納法から $B_{k+1}$ の構成方法は図の通り 3 つある。 union by rank, union by size いずれでも $B_k$ と $B_k$ を Union すると $B_{k+1}$ ができるから、Union Find の $2^{k}$ 回の合併で $B_k$ を作りだすことができる。

Union by Size の計算量

Union by Size とは、根付き木 A, B を Union するとき、頂点数の小さい方の木をもう一方の木の根の子とする方法である。

その構成方法から $2\mathrm{size}(u) \leq \mathrm{size}(\mathrm{parent}(u))$ が成り立つ。従って $O(\log{n})$ である。二項木 $B_k\ (2^k \sim n)\ $ は、高さ $ \Theta(\log n) $ であるから最悪ケースを与える。

Union by Rank の計算量

Union by Rank とは、根付き木 A, B を Union するとき、rank の小さい方の木をもう一方の木の根の子とする方法である。rank は（経路圧縮しないときの）木の高さとして定義する。

まず、ランク $r$ 以上の頂点を根とする部分木のサイズは $2^r$ 以上であることを帰納法で示す。

Union by Rank において、rank r の木のサイズは $2^r$ 以上である。

証明：数学的帰納法で示す。
(i) r = 0 のとき、木が 1 頂点からなるから成立する。
(ii) r = k で成立を仮定する。 rank k + 1 の木は形成過程で rank k の木同士を Union する。帰納法の仮定からランク k の木は頂点数 $2^k$ 以上だから、ランク k + 1 の木の頂点数は $2^{k+1}$ 以上である。従って r = k + 1 で成立。以上 (i), (ii) から帰納法により任意の r について成立する。

ランク $r$ の木のサイズについて $2^r \leq n$ より $r \leq \lfloor \log_2 n \rfloor $。ランクは高さと一致していたから find クエリと union クエリは共に $O(\log n)$ となる。二項木 $B_k\ (2^k \sim n)\ $ は、高さ $ \Theta(\log n) $ であるから最悪ケースを与える。

経路圧縮の計算量解析

経路圧縮(path compression) では Union が $O(1)$、Find がならし $O(\log N)$ であることを示す。path halving, splitting は同じように解析できるので扱わない。

分割統治による証明

木を上下に $N/2$ 頂点ずつに分けて、それぞれ $A, B$ と置く。N 元の union find に対して M 回の union / find を行った時の計算量を $T(N, M)$ と置く。$T(N, M)$ のうち、A の頂点同士を端点に持つ辺が Find のパスに含まれるのは $T(N/2, N)+O(N)$ 回。B の頂点に対しても同様。A と B の頂点を両端点に持つ辺は各Find のパスに高々 1 回しか含まれず $O(N)$ 回。従って、$T(N, N) \leq 2T(N/2, N)+O(N)$ より $T(N, N)=O(N \log(N))$ である。

ポテンシャルを使った証明

時刻 $t$ における頂点 $i$ の部分木のサイズを $\sigma_i(t)$、ポテンシャル関数を $\Phi(t):=4\sum_{i=1}^n \log \sigma_i(t)$ と置く。$0 \leq \Phi(t) \leq 4n\log n$ かつ $\Phi(0)=0$ である。

Union では繋ぎ合わせる根のポテンシャルの寄与しか変化せず、一回当たり $O(\log N)$ しか増加しない。Union では内部で 2 回 Find を行うから、Union でのポテンシャルの増分は Find に割り当てればよい。

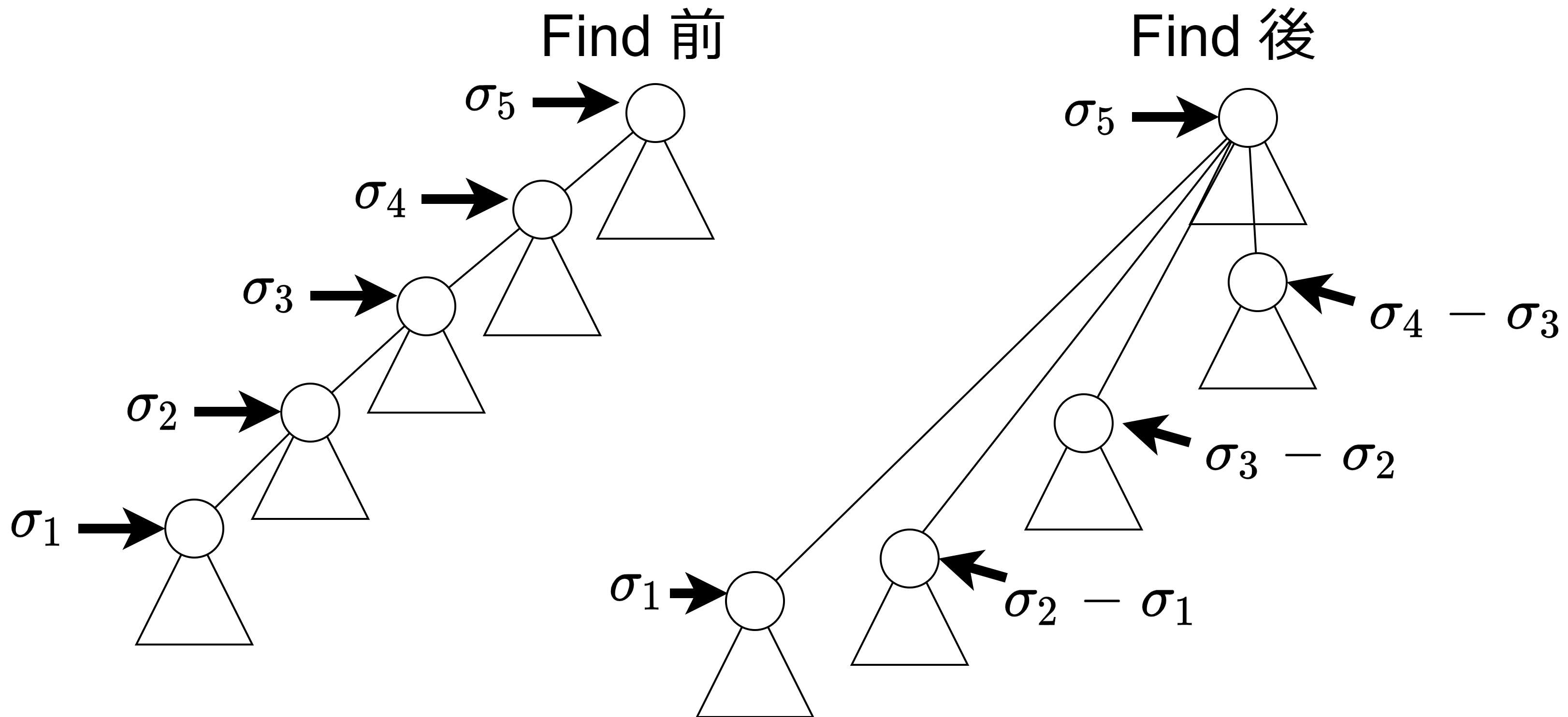
path_compression_potential

時刻 $t$ の Find において辿るパス上の頂点を根から遠い順に $\sigma_1,\sigma_2,\ldots,\sigma_k$ と置く（上図は k=5 の場合）。Find には根を見つけるのに $k$ ステップ、根を繋ぎ替えるのに $k-1$ ステップの合計 $2k-1$ ステップかかる。ポテンシャルの変化量は
$$
\begin{align}
H(t)-H(t-1)
=&4\sum_{i=2}^{k-1} \left(\log(\sigma_{i}-\sigma_{i-1})-\log\sigma_{i}\right)\\
=&4\sum_{i=2}^{k-1} \log\left(1-\frac{\sigma_{i-1}}{\sigma_i}\right)\\
\leq & – 4\sum_{i=2}^{k-1} \frac{\sigma_{i-1}}{\sigma_i}\
\end{align}
$$
で抑えられる（最後の不等号 $\log(1-x) \leq -x$ は原点での接線より）。$\frac{\sigma_{i}}{\sigma_{i+1}} \leq 1/2$なる $i$ が $m$ 個あるとする。$1 \leq \sigma_1 < \sigma_2 < \ldots < \sigma_k \leq n$ だから、$2^m \leq \sigma_k \leq n$ となり、$m \leq \log n$。従って

$-4\sum_{i=2}^{k-1} \frac{\sigma_{i-1}}{\sigma_i} < -4\cdot\frac{1}{2}(k-2-m) < -2k+4+4\log n$

より $H(t)-H(t-1)+2k-1=O(\log n)$ となるから Union はならし $O(\log n)$ である。

Path Compression の最悪ケース

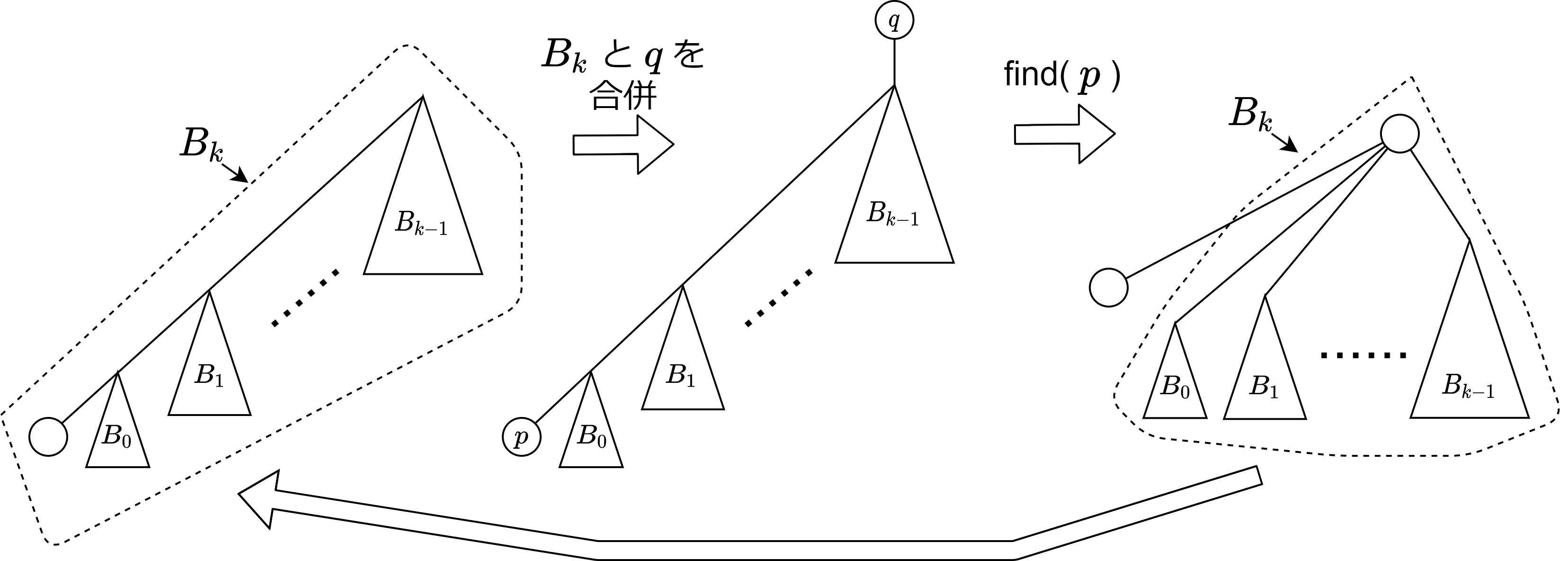
worstcase_dsu

$k=\Theta(\log(n))$ として、画像の操作を $\Theta(n)$ 回だけ繰り返すと Union と Find がならし $\Theta(\log n)$ となる。

Union by Rank, Size と経路圧縮の組み合わせ

Union by Rank (または Union by Size) と経路圧縮を組み合わせたとき、クエリ当りの計算量がアッカーマンの逆関数 $O(\alpha(n))$ となることが知られている。しかし、この証明は結構難しいので、評価を弱めて iterated logarithm $O(\log^*(n))$ で抑えられることを示そう[4]。iterated logarithm は $$ \log^* x :=
\begin{cases}
0 & \mbox{if } x \le 1; \\
1 + \log^*(\log x) & \mbox{if } x > 1
\end{cases}$$ で定義される。$x \in [\underbrace{b^{b^{\cdot^{\cdot^{b}}}}}_{y-1個}, \underbrace{b^{b^{\cdot^{\cdot^{b}}}}}_{y個})$ に対して $\log_b^*(x)=y$ である。

次の定理が Union by Rank のときに成り立つことは、「Union by Rank の計算量」の節で示した。Union by Size の場合について示す。

Union by Rank, Union by Size のどちらでも、rank r の木のサイズは $2^r$ 以上である。

証明：Union by Size において、rank k + 1 の木は形成過程で rank k の木 T’ を、別の木 T の根に部分木として繋いでいる。Union by Size より size(T’) ≦ size(T) であるから、rank k + 1 の木はサイズ $2^{k+1}$ 以上となる。

この定理から、頂点の個数は葉から遠いほど指数関数的に抑えられ、次の定理が成り立つ。

Union by Rank, Union by Size のどちらでも、rank r の頂点は高々 $n/2^r$ 個しかない。

例えば、完全 $m$ 分木 ($m \geq 2$) がこの条件を満たす。逆に、Path Comparession の worst case で上げた例は高さが $\Theta(n)$ あるので満たさない。長さ $\log(n)$ のパスが $n/\log(n)$ 本だけ根に接続した木も駄目である。定理を証明する。

証明：rank は経路圧縮しないときの高さであったから、（経路圧縮をしていても仮想的に）経路圧縮をしないときの木の形状を考える。任意のrank r の頂点の部分木は、部分木の根以外の頂点の rank が r 未満である。つまり、部分木の根以外に rank r の頂点が部分木に存在しない。従って、rank r の頂点を根とする部分木は互いに頂点を共有しない。この部分木のサイズが $2^r$ 以上であったから rank r の頂点は高々 $n/2^r$ 個しかない。

最終的に全ての頂点が Union によって連結になると仮定しても、計算量評価の一般性を失わない。Find によって、与えられた頂点から根まで辿るパスの辺の数を評価すれば良い。

頂点の集合 $s_k := \{v\ | \log_2^*(\mathrm{rank}(v))=k\}$ を定義する。Find によって辿るパス上の辺 (u, v) について、 u と v が異なる集合 $s_i$ に属しているとする。パス上の頂点の rank は根に近づくにつれて狭義単調増加するから、このような u, v はクエリ当り $O(\log^*(n))$ 個しかない。

従って、同じ集合 $s_i$ 内の２頂点を端点とする辺がいくつ Find のパスに含まれるか評価すれば良い。$B:=\underbrace{2^{2^{\cdot^{\cdot^{2}}}}}_{y-1個}$ と置く。rank r の頂点は高々 $n/2^r$ 個しかないので、$s_i$ のサイズは $\frac{n}{2^{B}}+\frac{n}{2^{B+1}}+\ldots+\frac{n}{2^{2^B-1}} < \frac{2n}{2^B}$ で抑えられる。パス上の頂点 u が根でも根の子でもないとする。すると、経路圧縮で頂点 u の親は rank が増加する。従って、Find のパスに u が含まれるクエリのうち、u の親が u と同じ $s_i$ に含まれるものは高々 $2^B – B + 1 < 2^B$ 個しかない。全体では $\sum_i 2^B \times \frac{2n}{2^B} = O(n \log^*n)$ 個である。Find のパス上の頂点のうち、根または根の子は高々２個しかないので、そのような頂点を端点に持つ辺の個数は計算量評価で無視しても良い。

以上より、Union by Rank, Size と経路圧縮を組み合わせるとならし $O(\log^*(n))$ になることが示された。

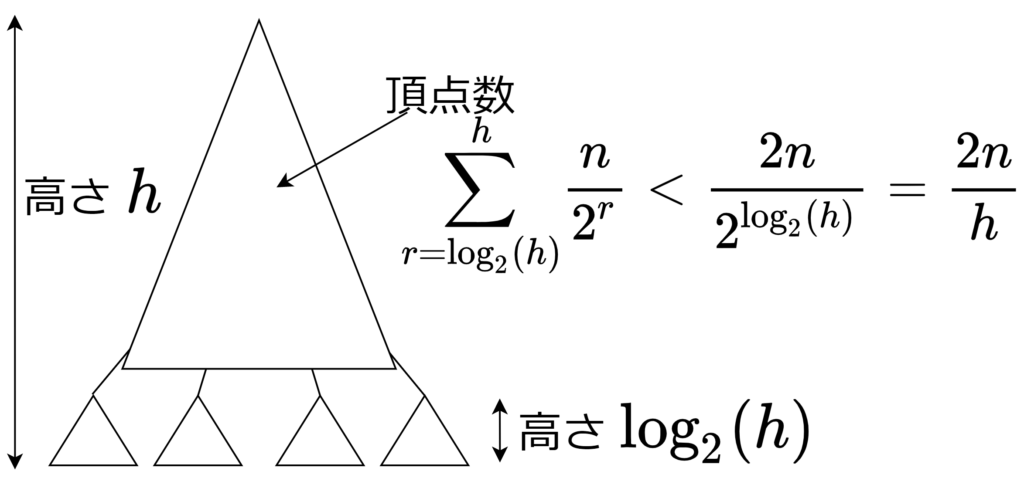
同じことだが、分割統治法で捉えることもできる[6]。ランク $h$ の森に対して、ランク $\log_2(h)$ を境に上下に分割する（下図）。ランク $\log_2(h)$ 以上の頂点の数は $\sum_{r=\log_2(h)}^h n/2^r < 2n/h$ で抑えられる。この頂点同士を端点に持つ辺が Find のパスに含まれるのは $O(h\times (2n/h)) = O(n)$ 回。ランク $\log_2(h)$ 以上の頂点と未満の頂点を端点に持つ辺は各Find のパスに高々 1 回しか含まれないから、操作全体で $O(n)$ 個。ランク $\log_2(h)$ 未満の森に対して分割統治を繰り返す。分割統治は $O(\log^*(h))$ 回繰り返せば終了するので、全体で $O(n\log^*(h))$ 時間。これは $i$ の降順に $s_i$ を評価していることと対応する。

そして$\alpha(n)$へ………

頂点数 $n$、ランク $h$ の木に対して $n$ 回の find を行った時の計算量を $T(n, h)$ とする。ランク $s-1$ 以上の頂点と未満の頂点で上下に分割すると、$O(n \log^*(n))$ のときと同様にして、計算量は
$$T(n, h) \leq T(n/2^{s},h) + n + T(n, s)$$となる。$T(n, h) \leq kng(n)$ とすると、$s=\log_2 (g(h))$ とすることで
\begin{align}
T(n, h) &\leq T(n/g(h),h) + n + T(n, \log g(h))) \\
&= kn + n + T(n, \log_2 g(h)) \\
&= (k+1)n(\log_2 g)^*(h)
\end{align}である。$T(n, h) = O(n \log^*(h))$ はすでに示した。$g(h) \leq 1$ となるまで $g \leftarrow (\log_2 g)^*$ を適用する回数は $O(\alpha(h))$ で抑えられるので、$k = O(\alpha(n))$ かつ $(\log g)^*(h) = O(1)$ とすることができ、$T(n, h) = O(n \alpha(n))$ である。

findを繰り返したときの計算量

union find で $\Theta(n\log(n))$ 回 find (union 内部のそれを含む）すると、ならし $O(1)$ になる。path compression を
無視した仮想的な木は、高さが $O(\log(n))$ になるから。Gabowらの最小全域有向木問題の高速化に Union Find のオーバーヘッドが掛からない理由がこれだった。

参考文献

Kevin Wayne 氏の授業スライド
- 図が豊富で分かりやすいです。アルゴリズムの挙動自体が分からないという場合はこちらを見ると良いと思います。
Alternative path compression techniques. van Leeuwen, J. van der Weide, R. (1977)
- paht halving を提唱した論文。計算量解析の部分を勉強しました。彼らは path halving + link by rank はクエリ当たりの計算量が iterated logarithm $\Theta(\log^* n) $ だと予想していたようです（実際はアッカーマンの逆関数）。
Fischer, Michael J. “Efficiency of equivalence algorithms.” Complexity of Computer Computations. Springer, Boston, MA, 1972. 153-167.
- path compression の計算量解析のために二項木を導入した論文。二項木のフラクタルな構造が面白いと思いました。
Hopcroft, John E., and Jeffrey D. Ullman. “Set merging algorithms.” SIAM Journal on Computing 2.4 (1973): 294-303.
- 計算量が iterated logarithm で抑えられることを示した論文。
Disjoint-set data structure – Wikipedia
Seidel, Raimund, and Micha Sharir. “Top-down analysis of path compression.” SIAM Journal on Computing 34.3 (2005): 515-525.

最悪計算量を最小化したUnion Find
- 永続化したい場合やオンラインで処理したい場合、ならしではなく最悪計算量を最小化した方が良いことがあります。ならし計算量 $O(\alpha(n))$ の Union Find は、最悪計算量が $\Theta(\log(n))$ になることがあります。この記事では最悪計算量 $O(\log(n)/\log\log(n))$ の Union Find を紹介しています。