2k正則グラフを2因子に分解

2-factor theorem と言われる、次の定理を証明します：

\(2k\)正則グラフである \(\Leftrightarrow\) \(k\)個の辺素な\(2\)因子で表せる

\(2\)因子は、全域\(2\)正則部分グラフのことです。このような「あるグラフのクラスが、ある操作で生成されるグラフ全体と一致する」というのはグラフ理論の醍醐味だと思います。

証明：
\(\Leftarrow\) は明らかです。ですから、\(\Rightarrow\) を示しましょう。\(2k\)正則グラフから1つ\(2\)因子を取り除くと\(2(k-1)\)正則グラフになります。従って、\(2k\)正則グラフは\(2\)因子を持つことを示せば十分。\(2k\)正則グラフは全ての頂点の次数が偶数だから、オイラー回路が存在します（証明）。オイラー回路を自然に向きづけて、有向回路にします。ポイントは各頂点 \(v\) を、辺が入る頂点 \(v^-\) と出る頂点 \(v^+\) に2分割することです。

\(v^-\) 同士には辺がないし、\(v^+\) 同士にも辺がないから、2部グラフになっています！　\(k\)正則\(2\)部グラフですから、Kőnigの定理より\(k\)個の\(1\)因子に分割できます。\(1\)因子を元のグラフに戻せば、次数が\(2\)倍になって\(2\)因子が得られます。

この定理はPetersenが1891年に示しました。Kőnigの定理が示された1931年から40年も前です。グラフ理論の黎明期でした。Petersenは何もないところから示す必要あったのです。Petersenの証明も見てみましょう。ステップ数は増えますが、創意工夫が感じられる証明だと思います。

証明：
Petersenは証明のためにswitchingという操作を考えました。辺AB, CDを消して、辺AC, BDあるいは辺AD, BCを追加する操作です。

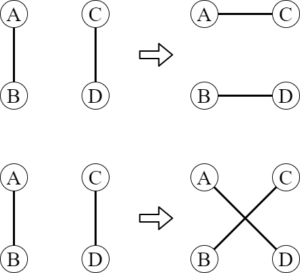A, B, C, Dで同じ頂点があっても構いません。switchingの逆操作もまた、switchingになっています。switchingは次の2つが成り立つという嬉しい性質があります：

switchingの前後で2因子を持つことが保存される。
switchingを繰り返すことで、任意の\(2k\)正則グラフに変形できる。

これらの事実から、2因子を持つことが自明なグラフにswitchingで変形してしまえます。自明に\(2\)因子を持つ\(2k\)正則グラフは例えば、多重サイクルがあります。

一つ一つ証明していきましょう。

switching後のグラフが2因子を持つなら、switching前も2因子を持つことを示します。辺AB, CDを辺AC, BDに変更したとしましょう。

switching後、辺AC,BDを同時に含む2因子がある場合、この2因子はswitching前もまた、2因子になっています。

switching後、辺AC,BDを同時に含む2因子が存在しない場合はどうなるのでしょうか。switching後、2因子に分解できるなら、辺AC, BDをそれぞれ含む２つの2因子があります。switching後、2因子に分解できるなら、辺AC, BDをそれぞれ含む2つの2因子があります。2因子の和は4因子になります。switching前に戻してもなお、4因子です。偶次数より、オイラー回路が取れます（証明）。握手補題より \(2E = \sum d(v)\) です。右辺が4の倍数だから、Eは偶数。オイラー回路の長さが偶数だから、辺を交互に割り当てて、2因子が二つ取れます。辺をAD, BCにするswitchingでも同様にして示せます。

次にswitchingを繰り返して、任意の\(2k\)正則グラフに変形できることを示しましょう。switching前のグラフをG、変形して作りたいグラフをFとします。switchingの逆操作もswitchingになっていました。したがって、G、Fの両方をswitchingして、同じグラフにできることを言えばいいです。対称差、つまり辺ごとのXORを取ります。各頂点にはGとFの辺が同じ個数だけ接続しています。DFSすれば、GとFの辺で交互に構成されたオイラー回路が取れます。特に、GとFが異なれば、長さ3の交互小道が取れます。５つのパターンがあります。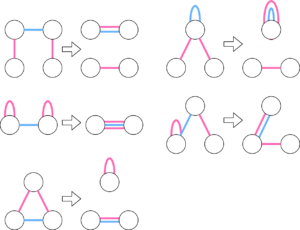どの場合も、対称差の辺の個数をswitchingで減らせます。辺の対称差が空集合になるまで、switchingを繰り返しましょう。Fを2因子を持つことが自明なグラフ、例えば、多重グラフにすれば、Gが2因子を持つことが言えました。