オイラーグラフの性質

全ての辺をちょうど一回通る回路が存在するとき、そのグラフはオイラーグラフであるといいます。また、そのような回路をオイラー回路といいます。慣習的にオイラー閉路と呼ばれることがありますが、閉路は各頂点の次数が2の連結グラフですから語義としては誤りだと思います。

オイラーグラフの特徴づけ

オイラーグラフであることの必要十分条件は、次の通りです：

オイラーグラフ $\Leftrightarrow$ 連結かつ全ての頂点の次数が偶数

証明しましょう。

（$\Rightarrow$の証明）オイラー回路の辺を辿って一周すると、頂点を通り抜けるたびに入る辺と出る辺を1つずつ使います（始点・終点はペアにする）。従って、各頂点の次数は偶数です。また、回路は連結なので、元のグラフ $G$ も連結です。

（$\Leftarrow$の証明）辺の数 $||G||$ に対する数学的帰納法で示します。$||G||=0$ つまり辺が存在しなければ、1頂点のオイラー回路が取れます。$||G||\geq 1$ とします。各頂点の次数が偶数なので、DFSにより回路 $W$ が取れます。$G-W$の各頂点は次数が偶数なので、帰納法の仮定より、各連結成分でオイラー回路が取れます。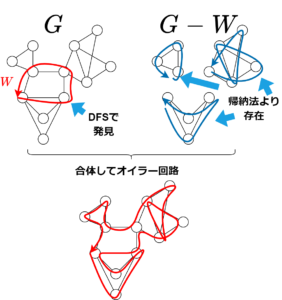元のグラフ $G$ の連結性より、各連結成分のオイラー回路は、回路 $W$ と繋ぎ合わせることで、一つの回路にできます。これはオイラー回路そのものです。

この証明はオイラー回路を求めるアルゴリズムも示しています。DFSで極大な回路として $W$ を取ると、通った辺の全てを $W$ に使えます（まだ通っていない辺が接続している限り、小道を閉じずにその辺を通ります）。各辺を一度しか通らず、回路の合体も $O(1)$ なので、$O(||G||)$ でオイラー回路が構築できます。

無向グラフにおけるオイラーグラフの母関数

頂点集合 $\{1, 2, \ldots, n+1\}$ 上の偶次数のグラフ（オイラーグラフから連結性を落としたグラフ）と、 $\{1, 2, \ldots, n\}$ 上のグラフの個数は等しいです。次の二つの操作が全単射になっています。

$n+1$ 頂点オイラーグラフから頂点 $n+1$ を削除する。
$n$ 頂点連結グラフ $G$ に頂点 $n+1$ を追加し、$G$ の奇点と頂点 $n+1$ に辺を張る。奇点は偶数個あるので、頂点 $n+1$ の次数は偶数になる。

あるグラフの指数型母関数を $f$, そのうち連結グラフに限った指数型母関数を $f_{conn}$ とすると、$f = \exp(f_{conn})$ の関係にあるので、$f_{conn} = \log(f)$ となる。グラフ全体の指数型母関数は$g = \sum_n 2^{{n \choose 2}} x^n/n!$ なので、オイラーグラフの指数型母関数は $\log((g-1)/x)$ となる。

有向グラフのオイラーグラフの数え上げ：BEST定理

$G$ を有向オイラーグラフとする。このとき、$G$のオイラー回路の個数は、根 $v$ へ向きづけられた有向全域木の個数を $t(G)$ として、$$t(G) \prod_{u \in V(G)} (d^+(u)-1)!$$に等しい。ただし $d^+(u)$ は $u$ の出次数である。オイラー回路の個数はは根 $v$ の選び方に依らないことから、$t(G)$ の値も $v$ に依らない。

証明：頂点 $v$ から出る辺を一つ選んで $e$ と置く。各オイラー回路について、$e$ から順に辺を辿る。このとき、各頂点 $w$ から出る最後に通る辺を $e_w$ と置く。このとき、$\{e_w : w \neq v\}$ がなす部分グラフは、頂点 $v$ へ向きづけられた有向木になる。なぜなら、どの頂点を始点としても、最後に通った出る辺を辿り続けることで $v$ に到達しなければならないからである。逆に、頂点 $v$ へ向きづけられた有向全域木 $T$ を定め、$T$ の辺を最後に通る出る辺とすれば、残りの出る辺の辿る順序を自由どのように定めても、オイラー回路が得られる。

$t(G)$ の数え上げは行列木定理によって $O(|V|^3)$ でできます。

Noga Alon の二部グラフの辺彩色
- オイラー回路が一つのカギになったアルゴリズムです。

参考文献

[1] A First Course in Graph Theory
[2] グラフ理論（R. Diestel）

Euler の名前が冠されていますが、彼が示したのは必要性（$\Rightarrow$）だけでした。十分性（$\Leftarrow$）を示したのは、Hierholzerです[1]。Euler & Heirholzerグラフと呼ぶべきかもしれません。