容量が整数の時に使える、藤重悟の最大流のアルゴリズムがある。容量の最大値を \(U\)、頂点数を \(N\)、辺数を \(M\) として \(O(NM \log(U))\) 時間で最大流が求まる。
アルゴリズム
次のような頂点列 \((v_1, v_2, \ldots, v_k)\) が得られたとする。
- 列の先頭がソース \(v_1 = s\) である。
- 列の末尾がシンク \(v_k = t\) である。
- 全ての \(i\) について \(v_1, v_2, \ldots, v_i\) から \(v_{i+1}\) に入る辺の残余容量の合計が \(\alpha\) 以上。
この頂点列の末尾から順に貪欲に流すことで流量 \(\alpha\) のフローが構成できる。この頂点列は次のように発見する。
- 初期状態の列を \((v_1) = (s)\) として次の操作を繰り返す。
- 列の末尾 \(v_i\) の隣接点 \(w\) であって \(v_1, v_2, \ldots, v_i\) から入る辺の容量の合計が \(\alpha\) 以上であるなら \(v_{i + 1} ← w\) とする。そのような \(w\) が存在しないか、\(v_{i + 1} = t\) となれば終了。
この操作で末尾 \(t\) の頂点列が見つかれば、流量 \(\alpha\) のフローを流す。見つからなければ、\(\alpha \leftarrow \lfloor \alpha / 2 \rfloor\) として、再度、頂点列を探索する。\(\alpha = 1\) として何度も上記の頂点列によるフローを流せば、いつか、最大流は求まる。
つまり次のようなアルゴリズムになる。
while (\(\alpha > 0\)) {
前述のフローを可能な限り流す。
\(α ← \lfloor α / 2 \rfloor\)
}
驚くことに、このとき \(O(NM\log(U))\) となるのだ。
計算量解析
\(\alpha \leftarrow \lfloor \alpha / 2 \rfloor \) となる直前の状態を調べよう。
\(S = \{v_1, v_2, \ldots, v_k \}\) とすると \( \forall w \in V \setminus S\) について、\(S\) から \(w\) に入る辺の残余容量の合計は \(\alpha\) 未満である。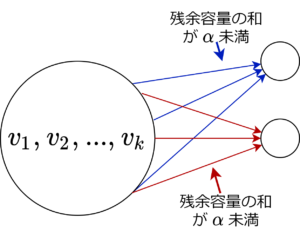
従って、残余ネットワークのカット \((S, V \setminus S)\) の大きさは \((N – k)\alpha\) 未満である。これは流量 \(\lfloor α / 2 \rfloor\) のフローが高々 \(3N\) 回しか見つからないことを意味している。よって、全体の計算量は \(O(NM \log U)\)。
参考文献
- 組合せ最適化（コルテ＆フィーゲン）
Comments