フィボナッチヒープとは
フィボナッチヒープは Dijkstra 法の計算量を改善する目的で、Fredman と Tarjan により発明されたヒープである。Dijkstra 法の計算量改善とは、decrease-key （キーの値の減少）を二項ヒープの \(O(\log(n))\) から \(O(1)\) にすることであった（\(n\) はヒープの要素数）。
| ヒープ | フィボナッチヒープ | 二項ヒープ | 二分ヒープ |
|---|---|---|---|
| キーの値を減少 | ならし \(O(1)\) | \(O(\log n)\) | \(O(\log n)\) |
| 値の追加 | ならし \(O(1)\) | ならし \(O(1)\) | \(O(\log n)\) |
| 2つのヒープの合体 | ならし \(O(1)\) | ならし \(O(1)\) | ならし \(O((\log n)^2)\) |
フィボナッチヒープ、二項ヒープ、二分ヒープの計算量の関係は上の図のようになる。
フィボナッチヒープのアイディア
頂点 \(v\) の decrease-key を \(O(1)\) にする単純な方法は、その頂点 \(v\) を根とする部分木を切り離してから decrease-key することである。こうすれば、頂点 \(v\) についての heap-property（親要素≦子要素）は壊れない。しかし、何度も切断を繰り返すと、木がアンバランスになって、ほかの操作の計算量が悪化してしまう。
そこで、根以外の頂点は、子を一つしか切り離せないとしたのがフィボナッチヒープである。
出次数 \(k\) の頂点 \(v\) から到達可能な頂点数の lower bound を \(L_k\) とする。手を動かしてみる（下画像）と、見事に、\(L_i\) が \(i + 2\) 番目のフィボナッチ数 \(F_{i+2}\) で下から抑えられていることが分かる。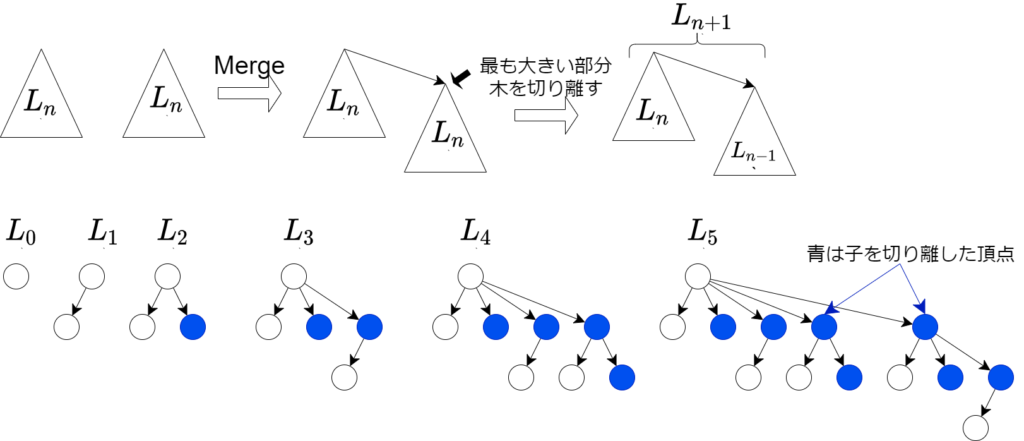
これが、”フィボナッチ”ヒープという名前の由縁である。
帰納法で \(L_k \geq F_{k+2}\) を示したい。\(k=0,1\) での成立は自明である。\(k \leq n\) での成立を仮定する。出次数 \(k\) の根 \(v\) には、出次数 \(k-1-\phi(v) \geq k-2\) 以上の子 \(u\) が存在し、辺 \((v, u)\) を削除すると、出次数 \(k-1\) の根 \(v\) と出次数 \(k-2\) の根 \(u\) に分かれる。辺を削除した後の \(v, u\) に対して帰納法の仮定を用いると、
\begin{align}
L_n &\geq L_{n-1}+L_{n-2} \\
& \geq F_{n+1}+F_{n} \\
& = F_{n+2}
\end{align}が得られ、\(k = n+1\) で成立。
ちなみに \(F_n=1+\sum_{i=0}^{n-2} F_i\) という分解を用いても示せる（考えてみよ）。
フィボナッチヒープでは以下の操作ができる。decrease-key 以外は、二項ヒープと同じアルゴリズムを用いている。
- insert(v)
- ならし \(O(1)\) 。ヒープに要素 \(v\) を追加する。
- find-min()
- 実時間 \(O(1)\) 。ヒープの最小要素を返す。
- delete-min()
- 実時間 \(O(\log(n))\) 。ヒープの最小要素を削除する。
- delete(v)
- 実時間 \(O(\log(n))\) 。要素 \(v\) を削除する。
- decrease-key(v, Δ)
- ならし \(O(1)\) 。要素 \(v\) のキーを \(\Delta\) だけ減算する。
- meld(h₁, h₂)
- ならし \(O(1)\) 。ヒープ中の二つの木 h₁, h₂ を合体する。
- meld(h)
- ならし \(O(1)\) 。別のヒープ h と合体する。
decrease-key
前述の通り、heap-property（親要素≦子要素）を保つため、decrease-key(v, Δ) では \(v\) と親を切り離してから、\(v\) のキーを \(Δ\) だけ減らす。木のバランスを保つために、根以外の頂点は、子を一度しか切り離せないという条件があった。もし、\(v\) の親 \(p\) がすでに子を切り離したことがあったならば、つまり、\(\phi(p) = 1\) であったならば、\(p\) は根でなければならない。そこで、\(\phi(p)=1\) であれば、再帰的に、\(p\) も親と切り離す。この操作を再帰的に繰り返す。
つまり、decrease-key(v, Δ) は次のようなアルゴリズムになる。
key(\(v\)) \(\leftarrow\) key(\(v\))\(-\)\(Δ\)
\(p \leftarrow \) parent(\(v\))
while (\(\phi(p)=1\)) {
\(p\) と parent(\(p\)) を切り離す。
\(p\) \(\leftarrow\) parent(\(p\))
}
\(\phi(p) \leftarrow 1\)
根を除いた \(\phi(v)=1\) となる頂点数は decrease-key の回数以下なので、再帰的に切り離す操作の回数も decrease-key の回数以下になる。よって、decrease-key はならし \(O(1)\) になる。
Comments