直径と中心とは
最も遠い2頂点間の距離を直径 \(\mathrm{diam}(G)\) という。また、最遠点までの距離が最小の頂点を中心と呼ぶ。
木の場合、中心と直径は頂点数に対して線形で求まる。同様のアルゴリズムを一般のグラフに適用すると、直径の2近似が得られる。
木の直径と中心を求めるアルゴリズム
自由な頂点 \(x\) の最遠点 \(y\) を求め、さらに \(y\) の最遠点 \(z\) を求める。最遠点は DFS により \(O(E+V)\) で求まる。このとき、\(\mathrm{dist}(y, z)\) が直径となる。木の場合、中心は \(y\)-\(z\) パスの真ん中にあるので、\(y\) を根とする木で \(z\) から親を \(\lfloor \mathrm{dist}(y,z)/2 \rfloor\) 回辿れば得られる。
最遠点を2回求めるので、このアルゴリズムは double-sweep と呼ばれている。アルゴリズムの正当性は次の通り。
\(x\) の最遠点を \(y\), \(y\) の最遠点を \(z\) とする。\(y\)-\(z\) が直径でないと仮定して矛盾を導く。
最長パス \(P\) を一つ固定する。
\(x\)-\(y\) パス と \(P\) が交わらない場合、図のように \(y\) を取り直すことで、\(x\)-\(y\) パスが長くなって矛盾(\(y\)が直径の端点でも、\(P\) と交わらないならば矛盾となる)。
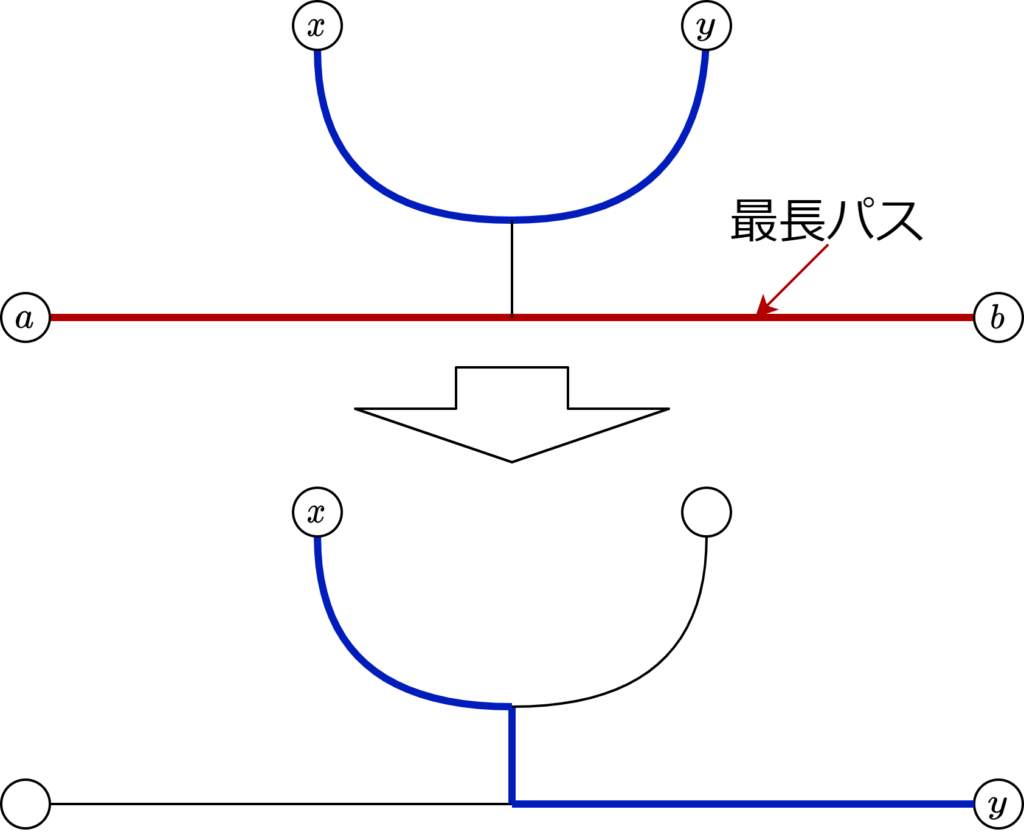
\(x\)-\(y\) パス と \(P\) が交わる場合も、図のように \(y\) を取り直すことで、\(x\)-\(y\) パスが長くなって矛盾。
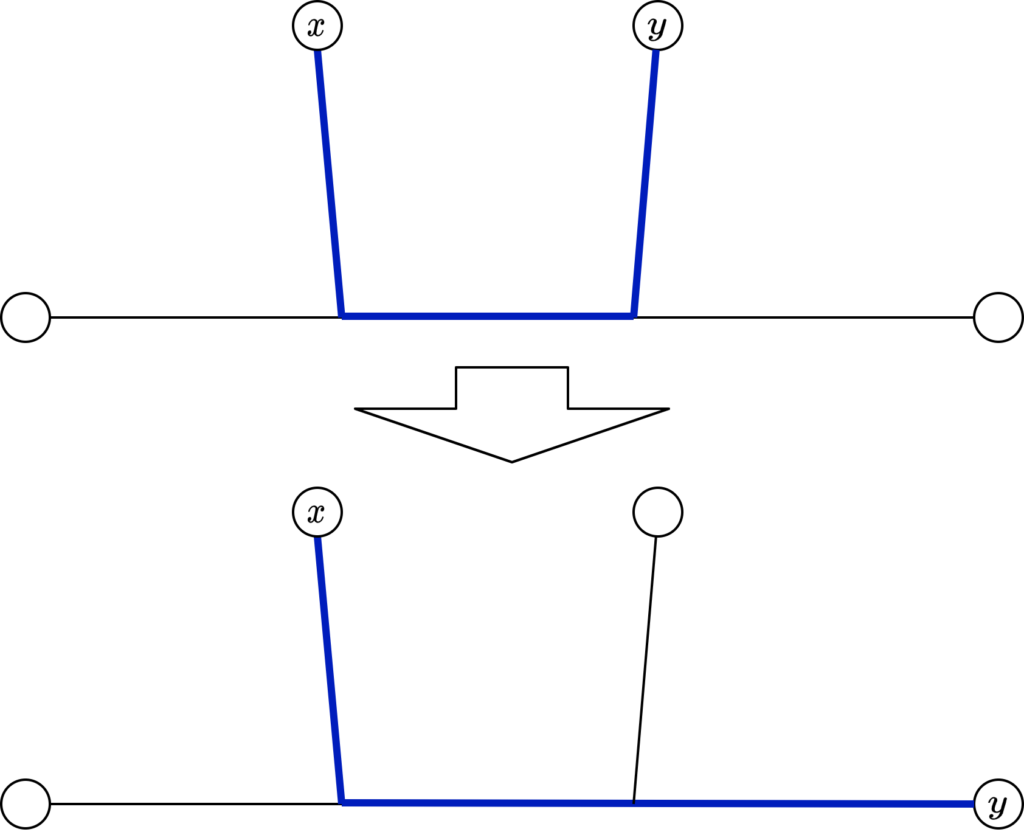
以上より、\(y\)-\(z\) の長さが直径となる。
37zigenの実装(Java)
以上の証明より、直径の端点 \(a, b\) に対し、任意の頂点 \(v\) は \(\max_w \mathrm{dist}(v, w) = \max(\mathrm{dist}(v, a), \mathrm{dist}(v, b))\) を満たすことが分かる。
2近似
前述の double sweep では、一般のグラフでは直径は求まらない。例えば、下図(maspyさんに教えてもらった)の \(x,y\) は互いに最遠点だが、\(\mathrm{dist}(x,y)\) は直径より小さい。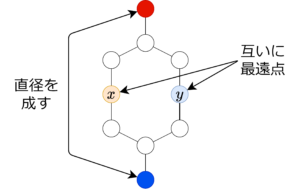
しかし、single sweep によって、直径の 2 近似を得ることは可能である(DFS は Dijskstra 法などに置き換える)。つまり、\(\mathrm{diam}(G) / 2 \leq d \leq \mathrm{diam}(G)\) を満たす \(d\) が得られる。
熨斗袋さんに証明を教えてもらった。
実際に近似率が2になるのは下図で、\(x, y\) の最遠点として \(y, x\) が見つかった場合。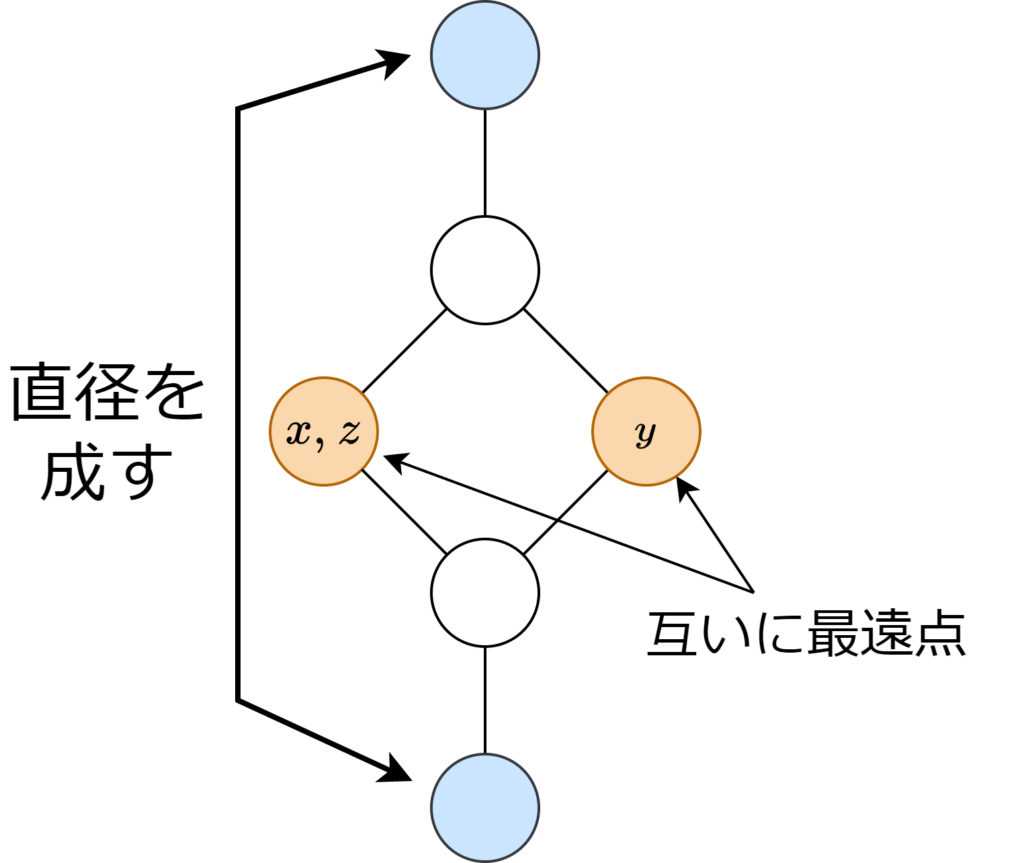
木の直径と中心の関係
木の中心は、直径が偶数の時一つ、奇数の時二つになり、どちらも直径の真ん中に位置する。各辺の真ん中にダミー頂点を追加すると、中心が一つの場合に帰着できる。つまり、辺 \((u,v)\) を \((u, x_{uv}), (x_{uv}, v)\) に分割すればよい。
Comments