- はまやんさんの最大流まとめ
- ferinさんのフローまとめ
- \(i\) 行目に駒は高々 \(a(i)\) 個
- \(j\) 列目に駒は高々 \(b(j)\) 個
- \(i\) 行目に同じ数字は高々 一つ
- \(j\) 列目に同じ数字は高々一つ
- \(s \Leftrightarrow \mathrm{True}\)
- \(t \Leftrightarrow \mathrm{False}\)
- \(p \land \overline{q}\) ならば罰金
- \(p\) ならば罰金
- \(\overline{p}\) ならば罰金
- \(p \lor \overline{q}\) である
- \(p \Rightarrow q\) である
- \((p_1 \lor \overline{q}_1) \land (p_2 \lor \overline{q}_2) \land \cdots \land (p_k \lor \overline{q}_k)\) である
- \(p \lor (\overline{q}_1 \land \overline{q}_2 \land \cdots \land \overline{q}_k)\) である
- \(p\Rightarrow q_1 \land q_2 \land \cdots \land q_k\) である
- \(p_1 \lor p_2 \lor \cdots \lor p_k \Rightarrow q \) である
- \(p_1 \lor p_2 \lor \cdots \lor p_k\) ならば罰金
- 以上の条件の各変数を否定に置き換えたもの。
- 以上の条件の論理積
- 以上の条件のうち、「\(P\) ならば罰金」の形のものを「\(\overline{P}\) ならば賞金」の形にしたもの
- \(t \in U\) なら増加路が存在すること
- \(W\) から \(U\) へ向かう辺の流量が 0 であること
- \(U\) から \(W\) へ向かう辺の流量が容量に等しいこと
- クエリ毎に独立に与えられる辺 \(e\) の容量を一つ増やす
- クエリ毎に独立に与えられる \(e\) の容量を一つ減らす
目次
マッチング
2部グラフの最大マッチングは最大流により求まる。これは色々拡張できる。
一方の部集合の一部の頂点 \(x_1,x_2,\ldots,x_k\) と もう一方の部集合の一部の頂点 \(y_1,y_2,\ldots,y_k\) の間に高々A本のマッチングが存在するという条件は、超頂点 z を用意して、容量 A の \((x_i, z)\) という辺と \((z,y_i)\) という辺を貼れば作れる(ABC205F)。
一方の部集合からもう一方の部集合へ集めるDPあるいは配るDPのように解釈すると、
という問題が解ける。
女の子を辺、男の子を頂点の次数とすると次の問題になる。
2部グラフの何かを構築する問題はマッチングに帰着できることがある。
特にグリッドグラフ(2部グラフ)で出題が多くある(例えば、天下一プログラマーコンテスト2015 予選A : C、yukicoder483)。
一部分が欠けたグリッドグラフに、
という条件を満たすように、与えられた個数の駒を置く問題は、行を一方の部集合の頂点、列をもう一方の部集合の頂点にするとマッチングに帰着できる。
これは、魔法陣に似ており、ラテン方陣の場合が次の形で Google Code Jam 2018 Round2 : C で出題されている。
という条件を満たすような部分グラフを求めよ。
行と列を部集合にする変わった問題には sugim さんの ARC047F がある。
カット
最大流の双対問題は最小カットである。
燃やす埋める
頂点集合の分割 \(V = V_1 \dot\cup V_2\) であって、\(s \in V_1, t \in V_2\) となるようなものを用いて、\(V_1\) から \(V_2\) に入る辺全体と表せる辺集合 \(F\) を s-t カットと呼びます。s-t カットは各頂点 \(v(\neq t)\) から出る辺の集合 \(\delta^+(v)\) を基底として持ち、辺 \(e\) がカットに採用される必要十分条件は \(e=(a,b) \in F \Leftrightarrow a \in V_1 \land b \in V_2\) です。最大流の大きさは最小カットの大きさに等しいので、最小カットを与える \(V_1, V_2\) を求めればよいです。議論の簡単のため、頂点を真偽値を取る変数と混同して、\(V_1\) の頂点に真、\(V_2\) の頂点に偽を割り当てると、\(e=(a,b) \in F \Leftrightarrow a \land \bar{b}\) となります。つまり、\(a \land \bar{b}\) ならば罰金 \(\mathrm{cost}(e)\) が必要という条件の元で、最小の \(V\) の論理値の割当をせよという問題に言い換えられます。
次のような表現が可能です。i,ii,iiiは前述の通り。
次のように構成します。
\(p_1 \Leftarrow p_2 \Leftarrow \cdots \Leftarrow p_k\) とすると
\((p_1,\ldots, p_k)=(\underbrace{\text{True}, \text{True}, ..,\text{True}}_{j 個}, \text{False}, \text{False}, \ldots, \text{False})\)
と \(j\) を対応させることで、\(0,1,\ldots,k\) と \((p_1,\ldots,p_k)\) との一対一対応を作れます。従って、上の表現は True/False の場合だけでなく、任意の整数値を取る場合にも拡張できます。
viii より、特殊な2SATは最大流で解けることが分かります。実用性はなさそうですが‥。
頂点被覆とは、任意の辺について少なくとも一方を被覆するような頂点集合のことです。頂点被覆に含まれる頂点には True、それ以外の頂点には False を割り当て、頂点と論理値を混同します。すると頂点被覆であることと、任意の辺 \(\{a, b\}\) について \(a \lor b\) が成り立つことが同値です。また頂点 \(v\) が頂点被覆に採用されるなら、頂点被覆の重みは \(\mathrm{cost}(v)\) だけ増えます。これは、\(v\) ならば罰金 \(\mathrm{cost}(v)\) と言い換えられます。ふつう、\(a \lor b\) はカットで表現できませんが、\(G\) が2部グラフなので、一方の部集合をすべて否定で置き換える(Falseならば頂点被覆に採用にする)と、前述の vi になります。従って、最小カットに帰着できました。最大流・最小カットの定理より、このグラフで最大流を求めればよいです。
つまり \(p_i\) iff \(x \leq i\) というような条件が扱えます。
各辺が非負整数となるように注意。
最小頂点カット
最大流最小カットの定理より、最小辺カットは最大流で求まりました。少し工夫することで、最小頂点カットも最大流で求まります。
有向グラフならば、各頂点 \(v\) を \(v_\mathrm{in}, v_\mathrm{out}\) に分割し、\(v\) に入る辺は \(v_\mathrm{in}\) に、出る辺 \(v_\mathrm{out}\) に接続して、元々あった辺の削除コストを \(\infty\)、\((v_\mathrm{in}, v_\mathrm{out})\) の削除コストを \(v\) の削除コストにします。すると、このグラフにおける最小辺カットの大きさが元のグラフの最小頂点カットになります。Mengerの定理の証明も参考にしてください。辺のコストを \(\infty\) にしなければ、頂点と辺を両方削除できるときの最小カットの大きさが求まります。
無向グラフの最小頂点カットは、単に各辺 \(\{u,v\}\) を双方向に移動できる2つの有向辺 \((u,v),(v,u)\) に置き換えて、有向グラフの場合に帰着すれば良いです。無向グラフにおいて、辺と頂点の両方を削除できる場合の最小カットは、Mengerの定理の証明でもやったように、下図のように \(v\leftrightarrow w\) の移動で必ず通る辺(↓)を用意して、その辺に元々の辺\((v,w)\)のコストを割り当てれば良いです。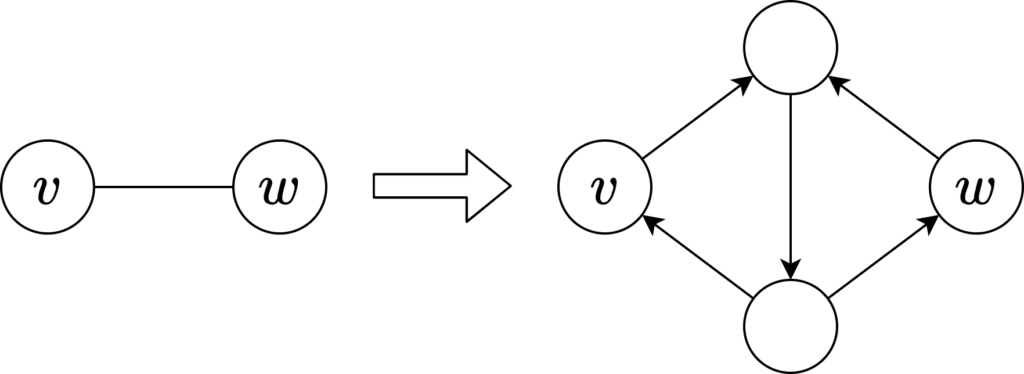
複数頂点間のカット
頂点集合 \(U\) に属する任意の2頂点を分離するような最小のカットも求まります。超頂点 \(s, t\) を作り、すべての頂点 \(v \in U\) に対して、\((s, v_{\mathrm out}),(v_{\mathrm in},t)\) という辺を貼ったグラフで s-t 最小辺カットを求めればよいです(DAGの少し違う場合 : WUPC2019F)。
最小カットの構造と復元
残余グラフで \(s\) から到達可能な頂点集合 \(U\) とその他の頂点 \(W=V \setminus U\) がなすカットが最小です。これは、
から分かります。
最小カットの構造については、CODE FESTIVAL 2015 エキシビション [A]が面白かったです。
カットを重みで分類
辺を2つの集合 \(A, B\) に分けて、\(A\) の辺の重みに十分大きな定数を足すと、\(B\) のみの辺を考えたときの最小カットの中で、\(B\) の辺のカットも最小にするものが求まります(東京工業大学プログラミングコンテスト2015L)。
平面グラフの最小カット
平面グラフの最小カットが高速に求まるらしいです。s, tが同じ面 F に属するときは、双対グラフで F を含む最短閉路を求めれば良いので、平面グラフの辺数が O(n) であることより、Dijkstra 法で O(n log(n)) です。同じ面に属さない場合は理解していません。
最小流量制限
各辺の最小流量を定めることができます。
snukeさん
近似的に求める
最大流に近いフロー F が高速に求まるなら、それを初期状態とすることで、残余グラフの更新回数を削減できる場合があります。F と最大流との流量の差を \(\Delta\) とすると、各辺の容量・流量が整数ならば、残余ネットワークにフローを流して、F を最大流にするのは \(O(\Delta E)\) でできます。
(出典 : Box Witch)
特殊なグラフの最大流
特殊なグラフの最大流を、普通よりも高速に求めよという問題が出ることがあります。最大流で考えにくければ、最小カットで考えてみるという程度のテクニックしか統一的なものは見当たりませんでした。
辺のコストが規則的な二部グラフ(ARC125E)
はしご状のグラフ
辺数の削減
次のような最大マッチング問題を考える。
次のような辺の張り方をすると、辺の個数を削減できる。
- ソース s から駒の置かれている頂点 v に流量 1 の辺を張る。
- G の任意の頂点 v からシンク t に流量 1 の辺を張る。
- G の任意の辺の流量を ∞ とする。
需給を主眼に考える
- 頂点対 \((a_i, b_i)\) が与えられる。好きな数 \(c_i \leq z_i \leq d_i\) を選び、\(c(a_i)\) に \(z_i\) を加算、 \(c(b_i)\) に \(z_i\) を減算する。
- [0, .., 0] に対して、i 番目のクエリで区間 [L[i], R[i]] に X[i] 以上 Y[i] 以下の数 A を加える。全要素が等しいという条件の下で作れる、要素の大きさの最大値を求めよ。(SRM 694 DIV1 Hard)
最密部分グラフ
\(\sum_{v \in S} d(v) = 2|\!|G[S] |\!|+ \delta(S)\) および \(\sum_{(u, v) \in S \times V \setminus S} 1 = \delta(S)\) だからコスト \(|\!| G[S] |\!|\) は最小カットで表せる(ARC161F)
Comments