Noga Alon の二部(多重)グラフの辺彩色のアルゴリズムを紹介する。計算量は辺数を \(E\) として \(O(E \log E)\) である。アルゴリズムがシンプルで気に入っている。
以下、「辺彩色」というと彩色数最小のものを指している事とする。
正則グラフに帰着
Kőnig の定理より二部グラフ \(G\) の最大次数 \(\Delta(G)\) と辺彩色数 \(\chi'(G)\) は等しい。つまり、最大次数を不変に保ったまま辺彩色が計算しやすいグラフに変形しても、彩色数が変化しない。
そこで、\(G\) を正則二部グラフに変形する。
合計の次数が最大次数 \(\Delta(G)\) 以下となるような同じ部集合内の \(2\) 頂点を合体する操作を可能な限り繰り返す。その後、孤立頂点を部集合のサイズが等しくなるように追加する。残った最大次数 \(\Delta(G)\) 未満の頂点は、辺を追加して次数 \(\Delta(G)\) にする。このとき、正則二部グラフになる。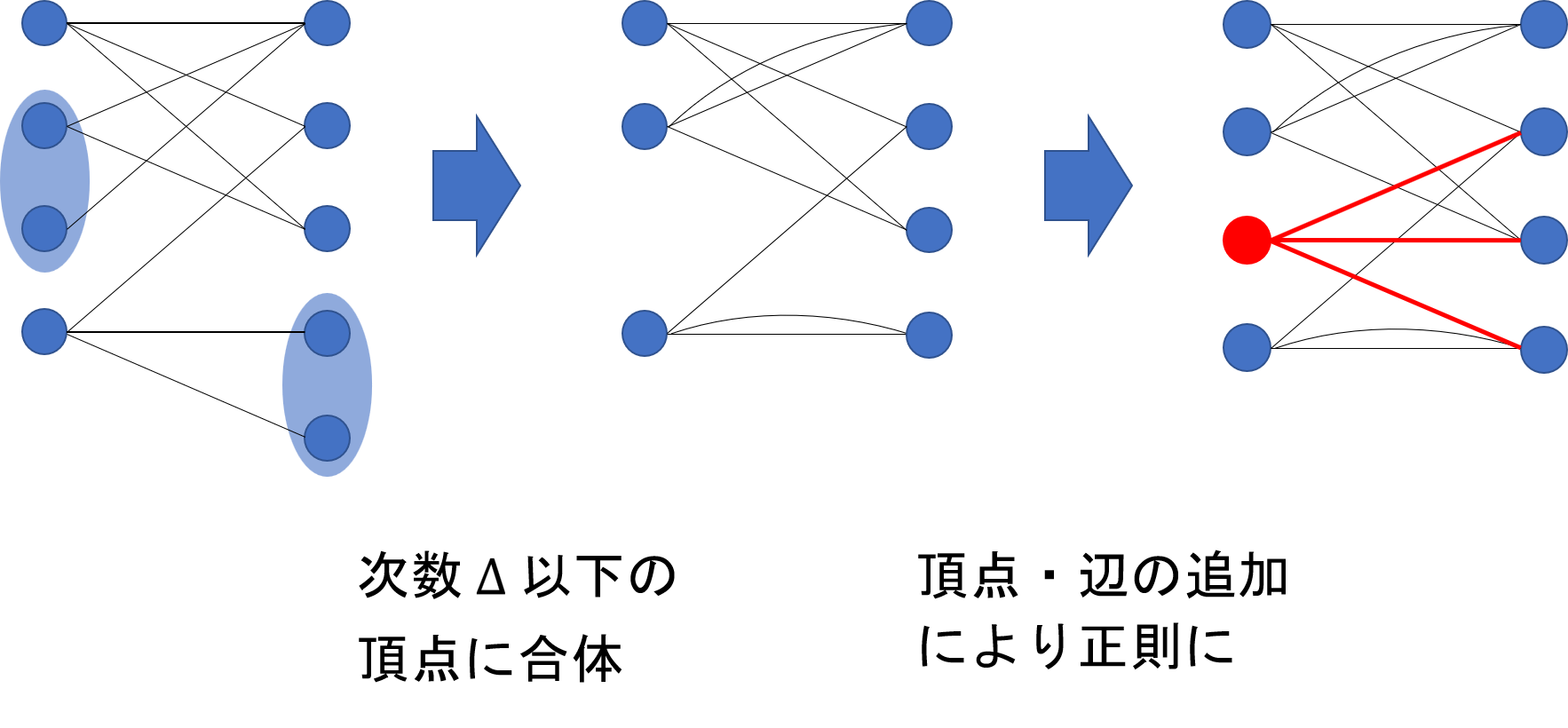
Kőnig の定理よりこのグラフ \(G’\) の辺彩色は、 \(G’\) の構成方法を逆に辿ることで、元のグラフ \(G\) の辺彩色を与える。従って、\(\Delta(G)\) 正則二部グラフ \(G’\) について辺彩色を求める問題に帰着された。辺数や頂点数のオーダーは変わっていないことに注意。
多重辺は単純グラフの辺に何個重複しているかを情報として載せることで表現することにする。この工夫は後で計算量改善に役立つ。
以下の事実を活用しながら辺彩色を求めていく。
\(2k\) 正則グラフは \(2\) つの \(k\) 正則グラフに分解できる
\(2k\) 正則グラフ \(H\) は \(2\) つの \(k\) 正則グラフ \(H_R, H_B\) に分解できる。全ての次数が偶数だからオイラー回路が取れて(証明)、辺を交互に \(H_R\) と \(H_B\) に割り当てればよい。二部グラフのオイラー回路であるから、\(H_R,H_B\) の次数は確かに全て \(k\) になる。
多重辺を同一視したときの辺数 \(F\) について \(O(F)\) でこの処理を行いたい。そこであらかじめ \(m(e)\) 個重複している辺 \(e\) は \(\lfloor m(e)/2\rfloor\) 個ずつ \(H_R,H_B\) に均等に振り分けておいて、単純グラフに帰着しておく。
この事実★をフル活用しながら、正則二部グラフの次数が偶数と奇数で場合分けして辺彩色を求める。
最大次数が偶数
上の事実★を用いて \(O(E)\) で \(2k\) 正則二部グラフ \(G\) を \(2\) つの \(k\) 正則二部グラフ \(H_R,H_B\) に分解する。\(H_R\) は再帰的に辺彩色を求める。その後、正則二部グラフの辺彩色は完全マッチングへの分割だから、\(H_R\) の辺彩色からいくつかの色の辺を取り去って \(H_B\) に加えることで次数を \(2\) 冪できる(下図)。
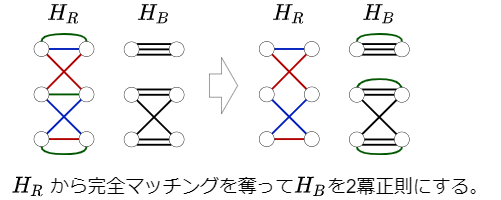
次数が \(2\) 冪だから、事実★を 1 正則二部グラフつまり完全マッチングになるまで適用することで \(H_B\) の完全マッチングが求められる(下図)。

最大次数が奇数
完全マッチングを一つ発見して取り去ることで、最大次数が偶数の場合に帰着する。完全マッチングは、\(k\) 正則二部グラフ G を \(2^t (\geq kn)\) 正則二部グラフに変形して、事実★を \(t\) 回適用することで見つける ( \(n\) は1つの部集合のサイズ)。\(2^t\) 正則への変形は \(G\) の各辺を\(\lfloor 2^t/k \rfloor\) 個の多重辺にしたあと、適当な完全マッチング \(W\) を \(2^t \bmod k\) 個加えることで実現する。\(W\) の辺数は \(2^t\) より小さいから、事実★を \(t\) 回適用する過程で常に \(W\) の本数が半減以上する方を選べば、最終的に得られる完全マッチングには \(W\) の辺が含まれない。
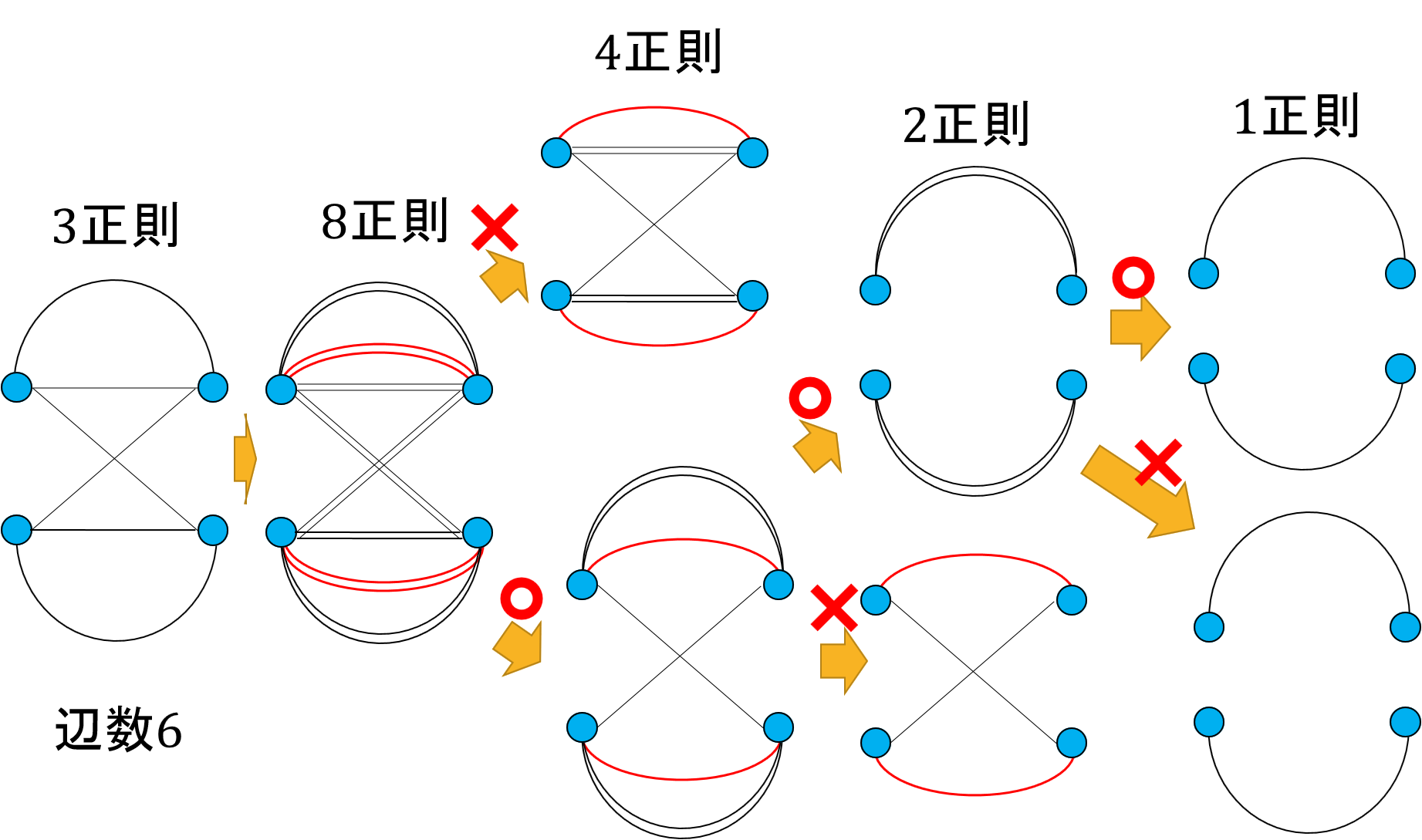
例えばこの図では適当な完全マッチング(赤色)を \(2\) 個加えることで \(2^3(\geq 6)\) 正則二部グラフに変換。その後事実★を \(3\) 回適用して赤辺が半減以上する方(赤丸)を選ぶことで完全マッチングを得る。
計算量解析
\(T(n,k)\) を 1 つの部集合のサイズが \(n\) の \(k\) 正則二部グラフの辺彩色を求めるのに必要な計算量とする。
\(k\) が偶数のとき、2つの正則二部グラフに分解するのに \(O(nk)\) 、一方の正則二部グラフの辺彩色を再帰的に計算するのに \(T(n,k/2)\) 、もう一方の正則二部グラフを2冪正則二部グラフに変換して辺彩色を求めるのに \(O(nk \log (nk) )\) だけかかるから、\(T(n,k)=O(nk \log (nk)) + T(n,k/2)\)。
\(k\) が奇数のとき、完全マッチングを見つけるのに必要な計算量は \(O(nk \log (nk))\) だから \(T(n,k)=O(nk \log (nk)) + T(n,k-1)\)。
以上を合わせて計算すると、\(T(n,k)=O(nk \log (nk))\) となる( \(E=O(nk)\) であることに注意)。
参考文献
- Alon, Noga. “A simple algorithm for edge-coloring bipartite multigraphs.” Information Processing Letters 85.6 (2003): 301-302.
- この記事で紹介したアルゴリズムの原論文です。
- R. Cole, K. Ost and S. Schirra, Edge-coloring bipartite multigraphs in \(O(E \log D)\) time, Combinatorica 21 (2001), 5-12.
- 僕の知る限り、計算量最速のアルゴリズムです。正則グラフに帰着するアイディアは既に使われています。内部で splay 木を使うなど実測は重そうな印象でした。
- よすぽジャッジの Edge Coloring of Bipartite Graph
- 二部グラフの辺彩色をプログラムで組んだ場合、ストレスチェックや速度の計測ができます。Forum を覗いてみると面白いかもしれません。このアルゴリズムの実装例も転がっています。
Comments