最小全域木(MST)と最短路木(SPT)は一般には等しくない。例えば、下図のMSTはコスト\(2\)だが、\(a\) を根とするSPTはコスト\(2.1\)である。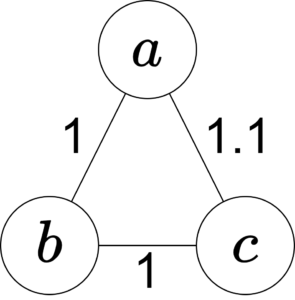
このコストの差は非常に大きくできる。Balancing minimum spanning trees and shortest-path trees.”では次のような例が使われている。以下\(r\)を根とする。
頂点 \(r, v, u_1, \ldots, u_L\) からなり、コストを\begin{align}
&c(\{r,v\})=2-\varepsilon/2 \\
&c(\{v,u_i\})=\varepsilon\ (i=1,2,\ldots,L) \\
&c(\{r,u_i\})=2\ (i=1,2,\ldots,L)
\end{align}とすると MSTでは \(\{r,v\}, \{v,u_i\}\) が採用され、SPTでは \(\{r,v\}, \{r,u_i\}\) が採用される。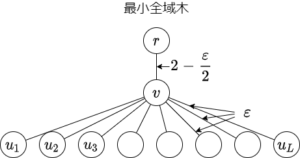
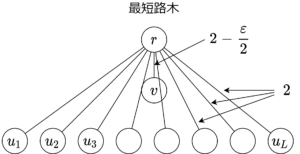
コストの比は \begin{align}
c(\mathrm{SPT}) / c(\mathrm{MST}) &= \frac{2-\varepsilon/2+\varepsilon L}{2(1+L)-\varepsilon/2} \\
&\to \infty \ (L \to \infty)
\end{align}となる。
\(∃v, \mathrm{dist}_{\mathrm{MST}}(r, v)/\mathrm{dist}_G(r, v) \to \infty \)となる例もある。頂点\(v_1, \ldots, v_n\)からなり、\(\{v_n,v_1\}\)のコストを\(2\)、それ以外を\(1\)とした\(n\)頂点閉路を考える。根を\(v_1\)とする。 \(v_{n}\)への距離の比は
\(v_{n}\)への距離の比は
\begin{align}
&\mathrm{dist}_{\mathrm{MST}}(r, v_n)/\mathrm{dist}_G(r, v_n) \\
= & \frac{2}{n-1} \\
\to & \infty \ (n \to \infty)
\end{align}となる。
MSTとSPTで好きな方に自由に寄せられる木として shallow light tree がある。
shallow light tree, \(T\) は
\begin{align}
&c(T) \leq (1+2\varepsilon^{-1})c(\mathrm{MST}) \\
&\mathrm{dist}_T(r, v) \leq (1+\varepsilon)\mathrm{dist}_G(r, v)\text{ for all } v
\end{align}を満たす木である。\(O(E+V\log(V))\) で構築できる。
アルゴリズム
- 最小全域木 \(T\) と最短路木 \(S\) を構築。\( R:= S \) とする。
- 根を \(v_0\) とする。\(T\) を DFS して、$$\mathrm{dist}_T(r, v_{i}) + \mathrm{dist}_T(v_{i}, v) > (1+\varepsilon)\mathrm{dist}_G(r, v)$$となる \(v\) が見つかる度に、\(S\) の \(r\)-\(v\) パスを \(R\) に追加、\(v_{i+1}:=v\) とする。
- R の最短路木 \(R’\) を求める。\(R’\) がshallow light treeになっている。
本音では \(\mathrm{dist}_R(r, v) > (1+\varepsilon)\mathrm{dist}_G(r, v)\) となる \(v\) についてだけ \(r\)-\(v\) パスを追加したいのだが、動的に変化する \(R\) の \(\mathrm{dist}_R(r, v)\) の計算を回避するために、上記のような方法で、余分にパスを追加している。
\(c(T)\) の評価は次の通り。
$$\mathrm{dist}_G(r,v_{i-1})+\mathrm{dist}_T(v_{i-1},v_i) \leq (1+\varepsilon)\mathrm{dist}_G(r,v_i)$$ の両辺で和を取ると \(2c(\mathrm{MST}) \leq \varepsilon \sum \mathrm{dist}_G(r,v_i)\) となり
\begin{align}
c(T) &= c(\mathrm{MST})+\sum\mathrm{dist}_G(r, v_i) \\
&\leq (1+2\varepsilon^{-1})c(\mathrm{MST})
\end{align} となる。
参考文献
- 組合せ最適化(コルテ&フィーゲン)
- 5版で shallow light tree が追加。輪読で shino さんにアルゴリズムを教えてもらった。
- Khuller, Samir, Balaji Raghavachari, and Neal Young. Balancing minimum spanning trees and shortest-path trees.” Algorithmica 14.4 (1995): 305-321.
- MSTとSPTの乖離が激しくなる例はこちらから取ってきた。
Comments