選択アルゴリズム：線形

数列 $(a_i)_{1 \leq i \leq n}$ が与えられたとき、昇順で $k$ 番目の項を $O(n)$ で見つける選択アルゴリズムを紹介します。決定的アルゴリズムは、乱択アルゴリズムを見てから方が分かりやすいと思います。

1 乱択アルゴリズム
2 決定的アルゴリズム
3 なぜ長さ 5 の数列に分割するのか
4 クイックソート
5 最小全域木
6 Soft Heap
7 関連記事

乱択アルゴリズム

ランダムに選んだ要素 $x$ が、昇順で $\frac{1}{4}n$ 番目から $\frac{3}{4}n$ 番目に含まれる確率はおよそ $\frac{1}{2}$ です。$x$ から線形時間で、 $x$ 以下の要素の集合 $A$、$x$ 未満の要素の集合 $B$ が求まります。発見したい $k$ 番目の要素は、$ k \leq A$ ならば $A$ の $k$ 番目、さもなくば $B$ の $k-|A|$ 番目にあります。従って、期待計算量 $T(n)$ は $T(n) \leq T(3n/4) + O(1)$ を満たします。この不等式を繰り返し適用すると、等比級数の公式より、$T(n) = O(n)$ が得られます。このアルゴリズムを脱乱択化するには、$x$ のような、元の数列の中央値の近似値があればよさそうです。

決定的アルゴリズム

数列 $a$ の昇順 $k$ 番目を返すアルゴリズムは次のようになります：

アルゴリズム $\mathrm{order}(a, k)$

$a$ を長さ $5$ の数列 $n/5$ 個に分けます。十分大きい数を $a$ に加えても（$k \leq n$ ならば）結果に変化はありませんから、オーダーを変えずに $n$ を $5$ の倍数だと仮定できます。
長さ $5$ の数列それぞれの中央値からなる長さ $n/5$ の数列 $c$ を作ります。
$c$ の中央値 $m=\mathrm{order}(c, \lfloor n/10 \rfloor)$ を見つけます。
$a$ を $m$ 未満、$m$ と等しい、$m$ 以上の要素からなる数列 $s_1,s_2,s_3$ に分割します。
次の３つのいずれかに場合分けします。

$k \leq |s_1|$ ならば
return $\mathrm{order}(s_1, k)$
$|s_1| < k \leq |s_1|+|s_2|$ ならば
return $m$
$|s_1|+|s_2| < k$ ならば
return $\mathrm{order}(s_1, k-|s_1|-|s_2|)$

計算量解析します。$m$ 以上の数は $3n/10$ 個以上、$m$ 以下の数も $3n/10$ 個以上あります。従って、$|s_1|, |s_3| \leq 7n/10$ です。このアルゴリズムの計算量を $T(n)$ と置くと、$$T(n)=T(n/5)+T(7n/10)+O(n)$$ です。$n/5+7n/10 < n$ より、等比級数の公式から $T(n) = O(n)$ を得ます。

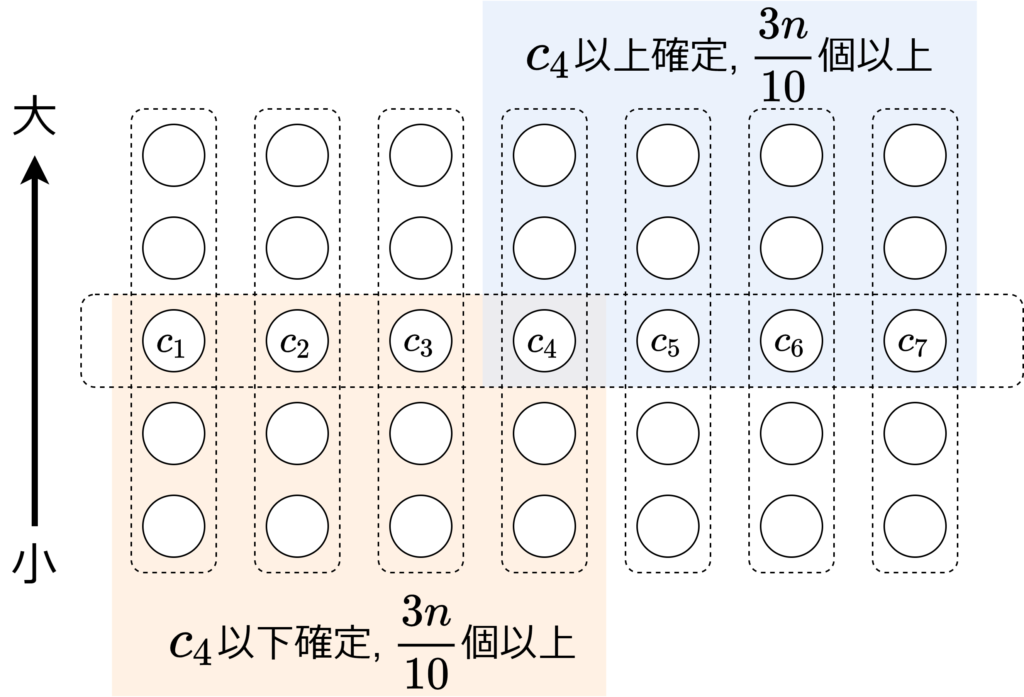
なぜ長さ 5 の数列に分割するのか

長さ $5$ の数列に分解しましたが、ほかの長さだとどうなるでしょうか。長さ $2d+1$ の数列に分解した場合、計算量は
$$T(n) = T\left(\frac{n}{2d+1}\right) + T\left(\left(1-\frac{d+1}{2(2d+1)}\right)n\right)+O(n)$$となります。解くと、$d=1$ のとき $T(n)=O(n\log(n))$, $d\geq 2$ のとき $T(n)=O(n)$ です。長さ 5 以上の奇数の数列に分解するのであれば、計算量はいつでも $O(n)$ になりました。

クイックソート

クイックソートのピボットを、このアルゴリズムで中央値に選ぶと、worst $\Theta(n\log(n))$ のソートができます。

最小全域木

最小全域木を線形時間で求める乱択アルゴリズムも似たアイディアを使っています。

Soft Heap

$\varepsilon n$ の誤差の下、$O(n \log(\varepsilon))$ で最小値を返すSoft Heapというデータ構造があります。この場合、オンラインで構築できる利点があります。

２次元線形計画問題：選択アルゴリズムを途中で用います。

定数個の数列に分割して、計算量改善するのはあまり見たことがなかったので驚き！