２変数の線形計画問題を \(O(n)\) (\(n\) : 条件の個数) で解くMegiddoのアルゴリズムを紹介します。
一般の線形計画問題は次の形で表されます：
線形計画問題：
行列 \(A \in \mathbb{R}^{n \times m}\) とベクトル \(\boldsymbol{b} \in \mathbb{R}^n, \boldsymbol{c} \in \mathbb{R}^{m}\) が与えられます。 \(A\boldsymbol{x} \geq \boldsymbol{b}\) の下、\(\min \boldsymbol{c}^T \boldsymbol{x}\) を与えるベクトル \(\boldsymbol{x} \in \mathbb{R}^m\) を求めてください。
行列 \(A \in \mathbb{R}^{n \times m}\) とベクトル \(\boldsymbol{b} \in \mathbb{R}^n, \boldsymbol{c} \in \mathbb{R}^{m}\) が与えられます。 \(A\boldsymbol{x} \geq \boldsymbol{b}\) の下、\(\min \boldsymbol{c}^T \boldsymbol{x}\) を与えるベクトル \(\boldsymbol{x} \in \mathbb{R}^m\) を求めてください。
2変数 \(m = 2\) がこの記事の問題です。特に、次の特殊な場合を考えます。この条件に \(l \leq x \leq r\) と \(\boldsymbol{c} \neq \boldsymbol{0}\) いう条件を加えると、一般の形になります。
二次元線形計画問題：
\(y \geq a_ix + b_i\) \((i=1, \ldots, m_1)\),
\(y \leq c_ix + d_i\) \((i=1, \ldots, m_2)\),
の下で、\(y\) の最小値を求めて下さい。
\(y \geq a_ix + b_i\) \((i=1, \ldots, m_1)\),
\(y \leq c_ix + d_i\) \((i=1, \ldots, m_2)\),
の下で、\(y\) の最小値を求めて下さい。
下図の通り、\(y \leq c_ix+d_i\) は上に凸な領域をなし、\(y \leq a_ix+b_i\) は下に凸な領域をなします。\(a_i, c_i\) でソートすると、各領域の包絡線が求まります。従って、\(O(n\log(n))\) で \(y\) の最小値が求まります。ここからは、\(O(n)\) で求めるアルゴリズムを紹介します。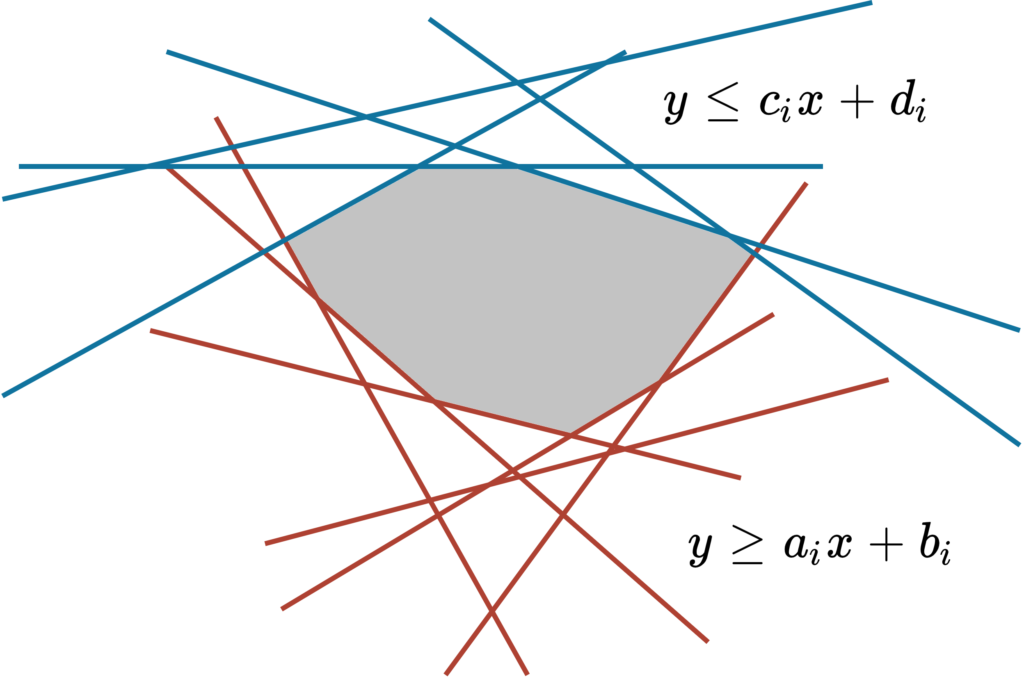
Megiddoのアルゴリズム
- 直線 \(y = a_ix+b_i\) を２つずつペアにし、直線 \(y=c_ix+d_i\) も２つずつペアにします。余りの直線は保留にしておきます。
- 各ペアの交点を列挙します。
- 交点の中央値 \(x^*\) を求めます。
- \(y\) の最小値を与える \(x\) 座標 \(x_m\) が、 \(x^*\) の左右どちらにあるか判定します。\(x_m\) が \(x^*\) のどちらにあるかは、２つの包絡線の \(y\) 座標の位置関係と傾きから分かります。
- 4. より軸 \(x=x^*\) に対して、左右どちらにあるか確定するペアがおよそ \(n/2\) 個あります（\(x^*\) が中央値より）。そのようなペアは直線の片方を捨てることができます。
- 残った直線について、再帰的に処理します。
選択アルゴリズムを用いると、3. の中央値が \(O(n/2)\) で求まります。
5. を説明します。交点が \(x_m\) の右側にある場合を考えます（下図）。\(y \leq a_ix+b_i\) の形のペアの場合、\(a_i\) の大きい方をすれてばよいです。\( y \geq c_ix+d_i\) の形のペアの場合、\(c_i\) の小さい方を捨てればよいです。
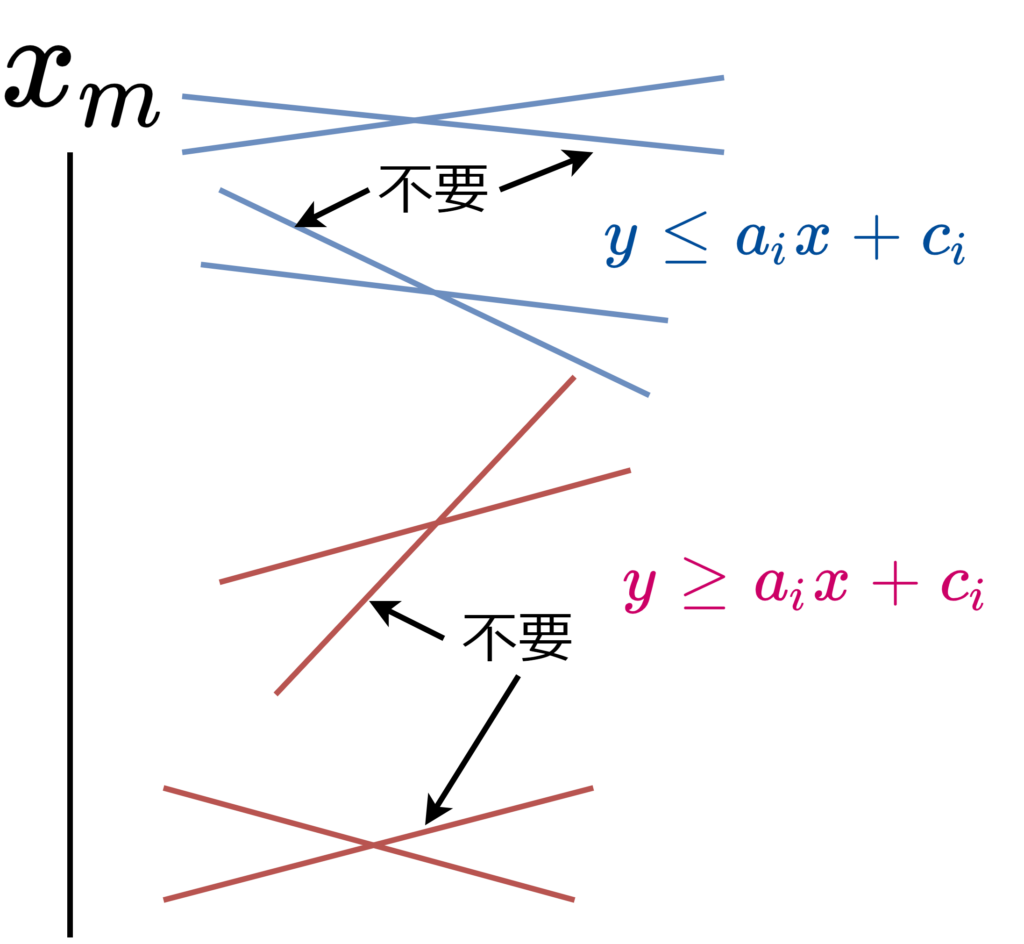
\(n\) 個の制約があるときに必要な計算量を \(T(n)\) とすると、\(T(n) = T(3n/4)+O(n/2)\) です。\(T(3n/4)\) がペアの一方を削除した部分問題の計算量、\(O(n/2)\) が中央値 \(x^*\) を見つけるのに必要な計算量です。解くと、\(T(n)=O(n)\) を得ます。
直線をペアにして考察するというのは初めて見ました。
Comments