「集合の合体（union）」と「要素の属す集合の発見（find）」を効率的に行うデータ構造 Union Find の解説をします。Union Find では次のクエリが高速に処理できます。

\(\mathrm{equiv}(a, b)\) は \(\mathrm{find}(a), \mathrm{find}(b)\) が等しいかどうかによって判定できます。

計算量はアッカーマンの逆関数 \(\alpha\) を用いてならし \(O(\alpha(n))\) 、最悪 \(O(\log(n))\) となります。

アルゴリズム

集合を根付き木で表します。同じ集合の元は同じ木の頂点です。

• 集合 ↔ 木
• 集合の要素 ↔ 木の頂点
• 集合の代表元 ↔ 木の根

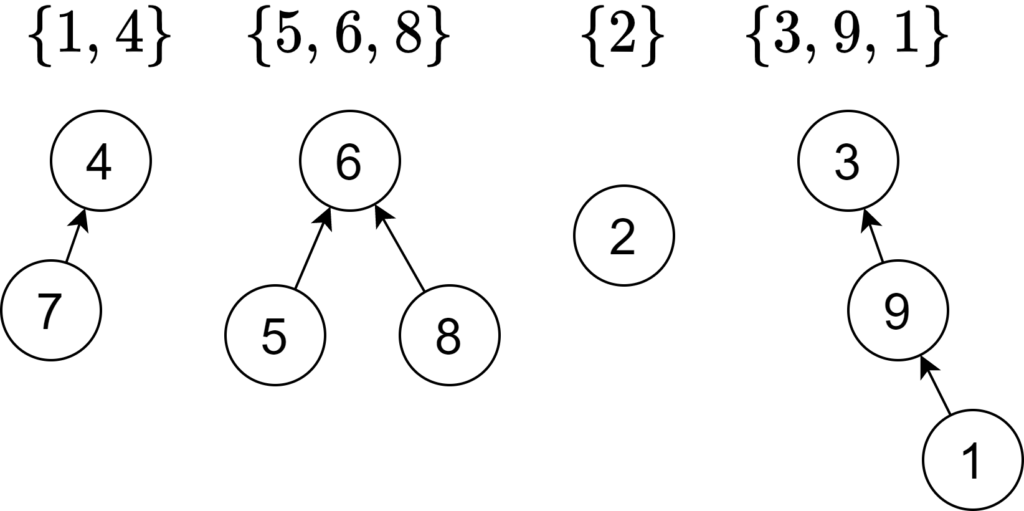
例えば、\(\{1,4\},\{5,6,8\},\{2\},\{1,3,9\}\) に対応する Union Find の木の一つに次のようなものがあります。代表元はそれぞれ \(4, 6, 2, 3\) です。

union

union(a, b) は a, b の属す二つの木を一つの木に合体させればよいです。一方の木の根を、もう一方の木の根の子とします。

find

find(a) は a の属す木の根（集合の代表元）を見つければよいです。a から親を辿れば height(a) ステップで根が見つかります。

union(a, b) は二つの木の根を繋ぐので、find(a) と find(b) を内包しています。根が見つかれば、繋ぐこと自体は \(O(1)\) です。従って find の計算量は union に完全に依存します。find は木の高さだけ計算量が必要でした。そこで、木の高さをできるだけ小さくすると find, union の計算量が小さくなります。木の高さを小さくするための工夫として、次に述べる Union by Size/Rank と Path Compression/Halving/Splitting があります。

ちなみに、ここでは紹介しませんが、根同士のリンクと find の計算量を平衡させて最悪計算量を最小化する k-uf という変種もあります。

Union By Size/Rank

木の頂点数が小さい方を子として、もう一方の木の根につなぐのが Union by Size です。また、木の高さが低い方を子として、もう一方の木の根につなぐのが Union by Rank です。

両方とも、単体では実時間 \(O(\log(n))\) / クエリ になります。これは、Union by Size/Rank では、親を辿るたびに部分木の大きさが二倍以上になり、木の高さが \(\log_2(n)\) で抑えられるからです。Union by Rank の場合、高さ \(k\) の木は高さ \(k-1\) の２つの木を Union したときにできます。従って帰納法により、親を辿るたびに部分木のサイズが二倍になることが言えます。Union by Size は構成法から明らかです。詳しい証明はUnion Find の計算量をご参照ください。

Find における高速化

find における高速化として、path compression, path halving, path splitting が知られています。いずれを使った場合も結果的な計算量は同じになるので、どれを使うかは好みだと思います。それぞれ単体ではならし \(O(\log(n))\) になり、union by size/rank と組み合わせるとアッカーマンの逆関数 \(O(\alpha(n))\) になります。詳しくは Union Find の計算量 をご覧ください。

Path Compression

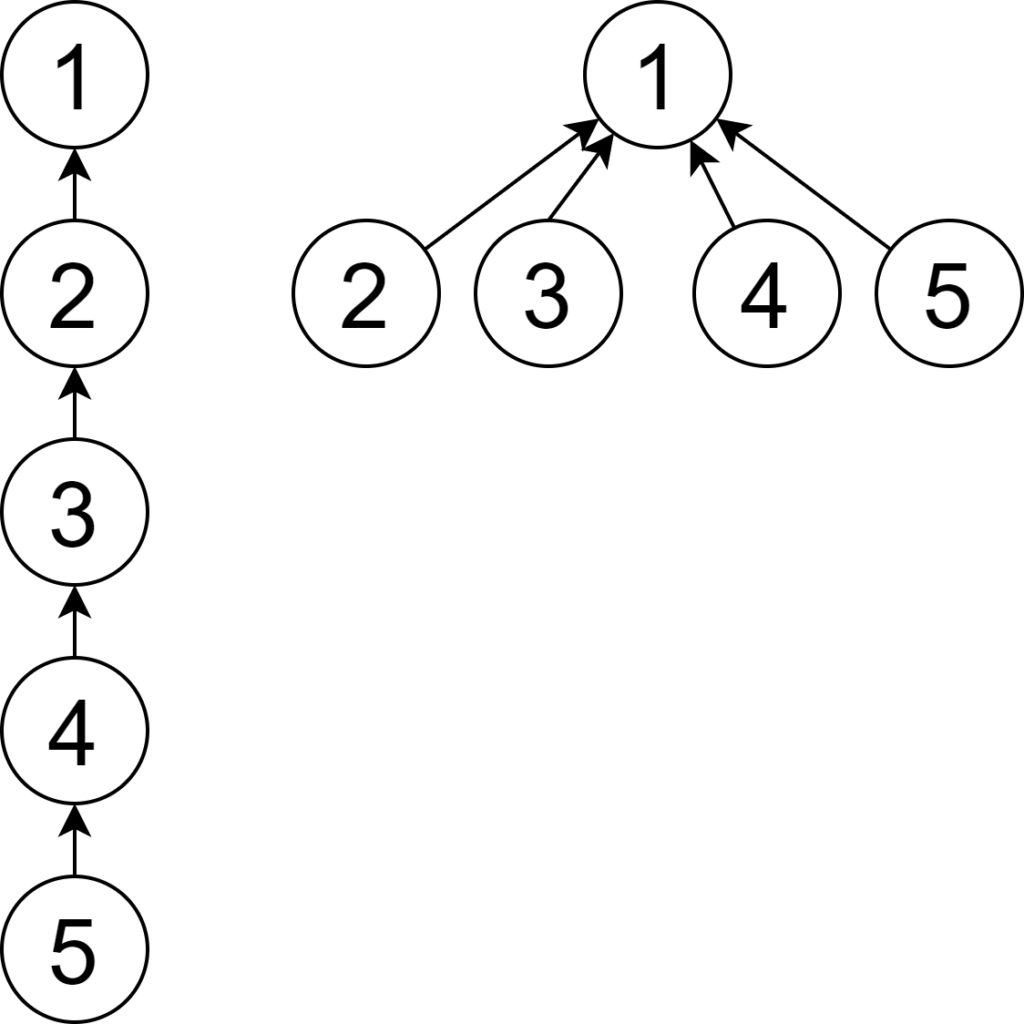find(x) としたとき、x から根までのパス上の頂点全てを、根に直接つなぐのが path compression です。C++のコードは次の通り。

int find(int x) {
    if (parent[x] == x) return x;
    else {
        parent[x] = find(parent[x]);
        return parent[x];
    }
}

Path Halving

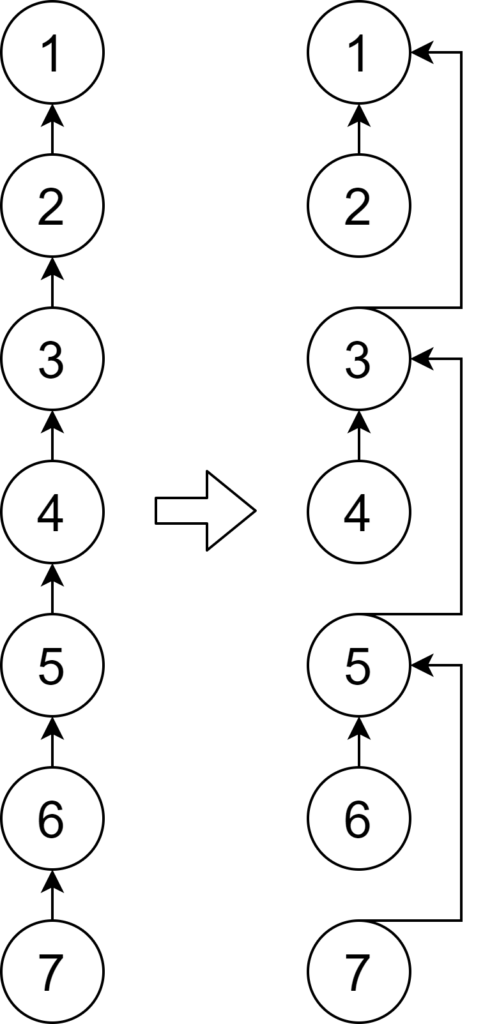find(x) としたとき、x と根を繋ぐパス上の頂点のうち高さ偶数のものを、祖父（親の親）につなぐのが path halving です。根の親は自分自身であるとすると実装が簡素になります。非再帰で書きやすいという特徴があります。C++のコードは次の通り。

int find(int x) {
    if (parent[x] == x) return x;
    else {
        parent[x] = parent[parent[x]];
        return find(parent[parent[x]]);
    }
}

Path Splitting

find(x) としたとき、x と根を繋ぐパス上の頂点を祖父（親の親）につなぐのが path splitting です。根の親は自分自身であるとすると実装が簡素になります。path halving と同じく、非再帰で書きやすいという特徴があります。C++のコードは次の通り。

int find(int x) {
    if (parent[x] == x) return x;
    else {
        int next = parent[x];
        parent[x] = parent[parent[x]];
        return find(next);
    }
}

C++の実装

union by size と path-splitting で実装した C++ のコードは次の通りです。union は予約語だったので merge にしています。

#include "vector"

using namespace std;

struct UnionFind {
  vector<int> parent; // parent[x]=y のとき、x の親が y
  vector<int> size;
  
  UnionFind(int n) {
    parent.resize(n);
    size.resize(n);
    for (int i = 0; i < n; ++i) parent[i] = i;//根は自分自身が親とする。
  }
  // x の属す集合の代表元を返す
  int find(int x) {
      if (parent[x] == x) return x;
      else {
          parent[x] = parent[parent[x]];// x の親を x の祖父とする
          return find(parent[parent[x]]);
      }
   }
  // x, y が属す集合を合体する
  void merge(int x, int y) {
    x = find(x);
    y = find(y);
    if (x == y) return;
    // マージテク
    if (size[x] < size[y]) swap(x, y);
    size[x] += size[y];
    parent[y] = x;
  }
  
  // x, y が同じに属すならtrue, さもなくば、false
  bool equiv(int x, int y) {
    return find(x) == find(y);
  }
};

演習問題

解答 : 隣接する頂点が同じ色にならないような、白と黒の２色の塗り分けが存在するか判定すれば良い。つまり、任意の辺 \((x, y)\) について、

• \(x\) は白、\(y\) は黒
• \(x\) は黒、\(y\) は白

のどちらかが成り立てば二部グラフである。各頂点 \(v\) について、白で塗った \(v_1\) と黒で塗った \(v_2\) を用意する。各辺 \(x, y\) について、\(x_1\) と \(y_2\)、\(x_2\) と \(y_1\) を同じグループに合体する。\(v_1, v_2\) が同じグループになるような頂点 \(v\) が存在しなければ2部グラフである。

解答 : グラフ \(G\) の連結成分の頂点集合を管理する Union Find の find を \(\mathrm{find}_{G}\) と書くことにします。
\(G_1, G_2\) の両方で \((x, y)\) が連結 \(\Leftrightarrow\) \((\mathrm{find}_{G_1}(x), \mathrm{find}_{G_2}(x))=(\mathrm{find}_{G_1}(y), \mathrm{find}_{G_2}(y))\) です。従って、\((\mathrm{find}_{G_1}(x), \mathrm{find}_{G_2}(x))\) が等しいものの個数を数えればよいです。基数ソートにより、この組は \(O()\) でソートできるので全体の計算量は \(O(|V|+|E|\alpha(|V|))\) です。

【一般論】\(S_k\) 上の同値関係 \(≡_k\) について、
\(a =_{R_k} b \Leftrightarrow \bigwedge_{i=1}^m (f_{i,k}(a) =_{R_{k-1}} f_{i,k}(b))\) が成り立つとする。サイズ \(n\) の同値類について\(x_i ≡_k x_j \ \ (1 \leq i, j \leq n) \Leftrightarrow x_1 ≡_k x_i\) \((1 \leq i \leq n)\) なので \(n\) 個の \(≡_{k}\) を \(≡_{k-1}\) に変換すればよい。従って Union Find により \(O(m\alpha(N)\sum|S_k|)\) で同値関係 \(≡_0\) に変換できる。また、次の条件を満たす場合を考える。

• \(S_k\) が \(k\) に依らない。
• \(a ≡_k b \Rightarrow a ≡_{k-1} b \)
• \(f_{i,k}\) が \(k\) に依らない。

このとき、\(O(\alpha(|S_0|)|S_0|)\) で同値関係 \(≡_0\) に変換できる（noshi91さん)。

• \(x^{(\alpha)} ≡_k y^{(\beta)} \Leftrightarrow x + \alpha i = y + \beta i\) \((1 \leq i \leq 2^k)\) とすると、\(≡_k\) は同値関係である。このとき、\(x^{(\alpha)} ≡_k y^{(\beta)} \Leftrightarrow x^{(\alpha)} ≡_{k-1} y^{(\beta)}\) かつ \((x+\alpha2^{k-1})^{(\alpha)} ≡_{k-1} (y+\beta2^{k-1})^{(\beta)} \)
• \(x^{(\alpha)} ≡_k y^{(\beta)} \Leftrightarrow x + \alpha i = y + \beta i\) \((1 \leq i \leq k)\) とすると、\(≡_k\) は同値関係である。このとき、\(x^{(\alpha)} ≡_k y^{(\beta)} \Leftrightarrow x^{(\alpha)} ≡_{k-1} y^{(\beta)}\) かつ \((x+\alpha)^{(\alpha)} ≡_{k-1} (y+\beta)^{(\beta)} \)

解答 : Union Find を \(\log_2(N)\) 個用意して、i 番目の Union Find を uf(i) と置く。uf(i).equiv(\(x, y\)) \(\Leftrightarrow\) \(x+j, y+j\) (\(0 \leq j < 2^i\)) が同じ集合とする。すると、sparse table と同様にすれば、高々２個の union でこの問題の連続する union が表せる。具体的には、\(w \leq 2^i\) となる最小の \(i\) を用いて、

• uf(i).union(\(x, y\))
• uf(i).union(\(x+w-1-2^i, y+w-1-2^i\))

とすれば良い。union が全て済んだら、その後、\(i=1\) まで伝搬すれば良い。

関連記事

Union Find の計算量
最悪計算量を最小化した Union Find
部分永続 Union Find